Hostname: page-component-77c89778f8-n9wrp Total loading time: 0 Render date: 2024-07-20T05:24:43.867Z Has data issue: false hasContentIssue false
  • English
  • Français

Poincaré and Friedrichs inequalities in abstract Sobolev spaces

Published online by Cambridge University Press:  24 October 2008

D. E. Edmunds ,
B. Opic  and
L. Pick
D. E. Edmunds
Affiliation:
Mathematics Division, University of Sussex
B. Opic
Affiliation:
Mathematical Institute, Czechoslovak Academy of Sciences, Prague, Czechoslovakia
L. Pick
Affiliation:
School of Mathematics, University of Wales, College of Cardiff
Get access Rights & Permissions [Opens in a new window]

Extract

Given any domain Ω in ℝN we consider spaces X = X(Ω),Y = Y(Ω) which are Banach function spaces in the sense of Luxemburg [12]. From these we form what we call the abstract Sobolev space W(X, Y), which is denned to be the linear space of all ƒ ∈ X such that for i = 1, …, N, the distributional derivative ∂ƒ/∂xi belongs to Y; equipped with the norm

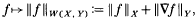
W(X, Y) is a Banach space. The closure of 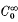(Ω) in W(X, Y) is denoted by W0(X, Y). Let w to bea weight function on Ω, that is, a measurable function which is positive and finite almost everywhere on Ω. We say that [w, X, Y] supports the (weighted) Poincaré inequality if there is a positive constant K such that for all u ∈ W(X, Y),

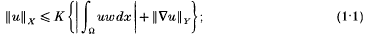
analogously, [X, Y] is said to support the Friedrichs inequality if there is a positive constant K such that for all u ∈ W0(X, Y),

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 113 , Issue 2 , March 1993 , pp. 355 - 379
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Amick, C. J.. Some remarks on Rellich's theorem and the Poincaré inequality. J. London Math. Soc. (2) 18 (1978), 81–93.CrossRefGoogle Scholar
[2]Canavati, J. A. and Galaz-Fontes, F.. Compactness of imbeddings between Banach spaces and applications to Sobolev spaces. J. London Math. Soc. (2) 41 (1990), 511–525.Google Scholar
[3]Edmunds, D. E. and Evans, W. D.. Spectral theory and embeddings of Sobolev spaces. Quart. J. Math. Oxford Ser. (2) 30 (1979), 431–453.CrossRefGoogle Scholar
[4]Edmunds, D. E. and Evans, W. D.. Spectral Theory and Differential Operators (Oxford University Press, 1987).Google Scholar
[5]Edmunds, D. E. and Opic, B.. Weighted Poincaré and Friedrichs inequalities. J. London Math. Soc., to appear.Google Scholar
[6]Goldberg, S.. Unbounded Linear Operators (McGraw-Hill, 1966).Google Scholar
[7]Gurka, P. and Opic, B.. Continuous and compact imbeddings of weighted Sobolev spaces I, II, III. Czechoslovak Math. J. 38 (133) (1988), 730–744; 39 (114) (1989), 78–94; 41 (116) (1991), 317–341.Google Scholar
[8]Krasnosel'skii, M. A. and Rutickii, J. B.. Convex Functions and Orlicz Spaces (Noordhoff, 1961).Google Scholar
[9]Krbec, M., Opic, B. and Pick, L.. Imbedding theorems for weighted Orlicz–Sobolev spaces. J. London Math. Soc., to appear.Google Scholar
[10]Kufner, A., John, O. and Fučík, S.. Function Spaces (Academia, 1977).Google Scholar
[11]Kufner, A.. Weighted Sobolev Spaces (Wiley, 1985).Google Scholar
[12]Luxemburg, W. A. J.. Banaoh function spaces. Thesis, Technische Hogeschool te Delft (1955).Google Scholar
[13]Opic, B.. Necessary and sufficient conditions for imbeddings in weighted Sobolev spaces. Časopis Pěst. Mat. 114 (1989), 165–175.Google Scholar
[14]Opic, B. and Kufner, A.. Hardy-type Inequalities. Pitman Research Notes in Mathematics, no. 219 (Longman Scientific and Technical, 1990).Google Scholar
[15]Wojtaszczyk, P.. Banach Spaces for Analysts. Cambridge Studies in advanced Math. no. 25 (Cambridge University Press, 1991).CrossRefGoogle Scholar
[16]Ziemer, W.. Weakly Differentiate Functions (Springer-Verlag, 1989).Google Scholar