Hostname: page-component-77c89778f8-gq7q9 Total loading time: 0 Render date: 2024-07-20T08:38:32.231Z Has data issue: false hasContentIssue false
  • English
  • Français

On the length formula of Hoskin and Deligne and associated graded rings of two-dimensional regular local rings

Published online by Cambridge University Press:  24 October 2008

Bernard L. Johnston  and
Jugal Verma
Bernard L. Johnston
Affiliation:
Department of Mathematics, Louisiana State University, Baton Rouge, LA 70803, Department of Mathematics, Florida Atlantic University, Boca Baton, FL 33431, U.S.A.
Jugal Verma
Affiliation:
Department of Mathematics, Louisiana State University, Baton Rouge, LA 70803, Department of Mathematics, Indian Institute of Technology, Powai, Bombay 400 076, India
Get access Rights & Permissions [Opens in a new window]

Extract

Let (R, m) be a 2-dimensional regular local ring and I an m-primary ideal. The aim of this paper is to find conditions on I so that the associated graded ring of I,

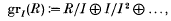
and the Rees ring of I,

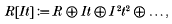
where t is an indeterminate, are Cohen–Macaulay (resp. Gorenstein). To this end, we use the results and techniques from Zariski's theory of complete ideals ([14], appendix 5) and its later generalizations and refinements due to Huneke [7] and Lipman[8]. The main result is an application of three deep theorems: (i) a generalization of Macaulay's classical theorem on Hilbert series of Gorenstein graded rings [13], (ii) a generalization of the Briançon–Skoda theorem due to Lipman and Sathaye [9], and (iii) a formula for the length of R/I, where I is a complete m-primary ideal, due to Hoskin[4] and Deligne[1].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 111 , Issue 3 , May 1992 , pp. 423 - 432
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Deligne, P. Intersections sur les surfaces régulières. In Groupes de Monodromie… (SGA7, II), Lecture Notes in Math. vol. 340 (Springer-Verlag, 1973), PP. 1–38.Google Scholar
[2]Goto, S. and Shimoda, Y.. On the Rees algebras of Cohen–Macaulay local rings. In Commutative Algebra (Analytic Methods), Lecture Notes in Pure and Applied Math. vol. 68 (Marcel Dekker, 1982), pp. 201–231.Google Scholar
[3]Herrmann, M., Ikeda, S. and Orbanz, U.. Equimultiplicity and Blowing-up: an Algebraic Study (Springer-Verlag, 1988).CrossRefGoogle Scholar
[4]Hoskin, M. A.. Zero-dimensional valuation ideals associated with plane curve branches. Proc. London Math. Soc. (3) 6 (1956), 70–99.CrossRefGoogle Scholar
[5]Huneke, C.. Hilbert functions and symbolic powers. Michigan Math. J. 34 (1987), 293–318.CrossRefGoogle Scholar
[6]Huneke, C.. On the associated graded ring of an ideal. Illinois J. Math. 26 (1982), 121–137.CrossRefGoogle Scholar
[7]Huneke, C.. Complete ideals in two-dimensional regular local rings. In Commutative Algebra, Proc. Microprogram, MSRI publication no. 15 (Springer-Verlag, 1989), pp. 325–328.CrossRefGoogle Scholar
[8]Lipman, J.. On complete ideals in regular local rings. In Algebraic Geometry and Commutative Algebra, Proceedings of a Conference in Honor of M. Nagata, vol. 1 (Academic Press, 1988), pp. 203–231.CrossRefGoogle Scholar
[9]Lipman, J. and Sathaye, A.. Jacobian ideals and a theorem of Briançon–Skoda. Michigan Math. J. 28 (1981), 199–222.CrossRefGoogle Scholar
[10]Matsumura, H.. Commutative Ring Theory (Cambridge University Press, 1986).Google Scholar
[11]Northcott, D. G.. Abstract dilatations and infinitely near points. Proc. Cambridge Philos. Soc. 52 (1956), 178–197.CrossRefGoogle Scholar
[12]Rees, D.. Hilbert functions and pseudo-rational local rings of dimension two. J. London Math. Soc. (2) 24 (1981), 467–479.CrossRefGoogle Scholar
[13]Stanley, R.. Hilbert functions of graded algebras. Adv. in Math. 28 (1978), 57–83.CrossRefGoogle Scholar
[14]Zariski, O. and Samuel, P.. Commutative Algebra, vol. 2 (Van Nostrand, 1960).CrossRefGoogle Scholar