Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-01T07:43:32.298Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Orientable Lagrangian Fillings of Legendrian Knots

Part of: Symplectic geometry, contact geometry

Published online by Cambridge University Press:  27 September 2023

LINYI CHEN ,
GRANT CRIDER-PHILLIPS ,
BRAEDEN REINOSO ,
JOSHUA SABLOFF  and
LEYU YAO
LINYI CHEN
Affiliation:
Google, Inc., 1021 Valley Street, Seattle, WA 98019, U.S.A. e-mail: chenlinyi1996@gmail.com
GRANT CRIDER-PHILLIPS
Affiliation:
University of Oregon, 1585 E 13th Ave, Eugene, OR 97403, U.S.A. e-mail: criderg@uoregon.edu
BRAEDEN REINOSO
Affiliation:
Boston College, Department of Mathematics, Maloney Hall Fifth Floor, 21 St Thomas More Road, Chestnut Hill, MA 02467, U.S.A. e-mail: reinosob@bc.edu
JOSHUA SABLOFF
Affiliation:
Haverford College, Department of Mathematics, 370 Lancaster Ave, Haverford, PA 19041, U.S.A. e-mail: jsabloff@haverford.edu
LEYU YAO
Affiliation:
University of Cambridge, Department of Applied Mathematics and Theoretical Physics, Wilberforce Road, Cambridge CB3 0WA. e-mail: ly339@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate when a Legendrian knot in the standard contact 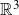${{\mathbb{R}}}^3$ has a non-orientable exact Lagrangian filling. We prove analogs of several results in the orientable setting, develop new combinatorial obstructions to fillability, and determine when several families of knots have such fillings. In particular, we completely determine when an alternating knot (and more generally a plus-adequate knot) is decomposably non-orientably fillable and classify the fillability of most torus and 3-strand pretzel knots. We also describe rigidity phenomena of decomposable non-orientable fillings, including finiteness of the possible normal Euler numbers of fillings and the minimisation of crosscap numbers of fillings, obtaining results which contrast in interesting ways with the smooth setting.

MSC classification

Secondary: 53D12: Lagrangian submanifolds; Maslov index
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 176 , Issue 1 , January 2024 , pp. 123 - 153
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Partially supported by NSF grant DMS-1406093 during the preparation of this paper.

‡

Partially supported by grants from Haverford College.

References

REFERENCES

Atiponrat, W.. $(4,-(2\textrm{n}+5))$ -torus knot with only 1 normal ruling. Preprint arXiv:1512.08057 (2015).Google Scholar
Atiponrat, W.. An obstruction to decomposable exact Lagrangian fillings. Preprint arXiv:1512.08056 (2015).Google Scholar
Batson, J.. Nonorientable slice genus can be arbitrarily large. Math. Res. Lett. 21(3) (2014), 423–436.CrossRefGoogle Scholar
Blackwell, S., Legout, N., Leverson, C., Limouzineau, M., Myer, Z., Pan, Y., Pezzimenti, S., Simone Suárez, L. and Traynor, L.. Constructions of Lagrangian cobordisms. Research directions in symplectic and contact geometry and topology. Assoc Women Math. Ser., 27 (Springer, 2021), pp. 245–272.Google Scholar
Boileau, M. and Orevkov, S.. Quasi-positivité d’une courbe analytique dans une boule pseudo-convexe. C. R. Acad. Sci. Paris Sér. I Math. 332(9) (2001), 825–830.Google Scholar
Bourgeois, F., Sabloff, J. M. and Traynor, L.. Lagrangian cobordisms via generating families: Construction and geography. Algebr. Geom. Topol. 15(4) (2015), 2439–2477.Google Scholar
Cahn, P., Classical invariants of legendrian and transverse knots. Encyclopedia of Knot Theory (Allison Henrich Louis H. Kauffman Lewis D. Ludwig Sam Nelson Colin Adams, Erica Flapan, ed.), (CRC Press, 2021), pp. 393–402.Google Scholar
Capovilla–Searle, O. and Traynor, L.. Nonorientable Lagrangian cobordisms between Legendrian knots. Pacific J. Math. 285(2) (2016), 319–343.Google Scholar
Chantraine, B.. On Lagrangian concordance of Legendrian knots. Algebr. Geom. Topol. 10 (2010), 63–85.Google Scholar
Chantraine, B.. A note on exact Lagrangian cobordisms with disconnected Legendrian ends. Proc. Amer. Math. Soc. 143(3) (2015), 1325–1331.Google Scholar
Chekanov, Y. and Pushkar, P. E.’. Combinatorics of Legendrian links and the Arnol’d 4-conjectures. Russ. Math. Surv. 60(1) (2005), 95–149.Google Scholar
Cornwell, C., Ng, L. and Sivek, S.. Obstructions to Lagrangian concordance. Algebr. Geom. Topol. 16(2) (2016), 797–824.CrossRefGoogle Scholar
Dimitroglou Rizell, G.. Legendrian ambient surgery and Legendrian contact homology. J. Symplectic Geom. 14(3) (2016), 811–901.Google Scholar
Dimitroglou Rizell, G.. Lifting pseudo-holomorphic polygons to the symplectisation of $P\times \mathbb{R}$ and applications. Quantum Topol. 7(1) (2016), 29–105.Google Scholar
Ekholm, T., Rational SFT, linearized Legendrian contact homology, and Lagrangian Floer cohomology. Perspectives in analysis, geometry and topology. Progr. Math. 296, (Birkhäuser/Springer, New York, 2012), pp. 109–145.Google Scholar
Ekholm, T., Honda, K. and Kálmán, T.. Legendrian knots and exact Lagrangian cobordisms. J. Eur. Math. Soc. (JEMS) 18(11) (2016), 2627–2689.CrossRefGoogle Scholar
Eliashberg, Y.. Topology of 2-knots in ${\bf R}^4$ and symplectic geometry. The Floer memorial volume. Progr. Math. 133, (Birkhäuser, Basel, 1995), pp. 335–353.Google Scholar
Eliashberg, Y. and Gromov, M.. Lagrangian intersection theory: finite-dimensional approach. Geometry of differential equations. Amer. Math. Soc. Transl. Ser. 2 186. (Amer. Math. Soc., Providence, RI, 1998), pp. 27–118.Google Scholar
Epstein, J. and Fuchs, D.. On the invariants of Legendrian mirror torus links. Symplectic and contact topology: interactions and perspectives (Toronto, ON/Montreal, QC, 2001). Fields Inst. Commun. 35, (Amer. Math. Soc., Providence, RI, 2003), pp. 103–115.Google Scholar
Etnyre, J. B.. Legendrian and transversal knots. Handbook of knot theory (Elsevier B. V., Amsterdam, 2005), pp. 105–185.Google Scholar
Etnyre, J. B. and Honda, K.. Knots and contact geometry I: Torus knots and the figure eight knot. J. Symplectic Geom. 1(1) (2001), 63–120.Google Scholar
Fuchs, D. and Ishkhanov, T.. Invariants of Legendrian knots and decompositions of front diagrams. Mosc. Math. J. 4(3) (2004), 707–717.CrossRefGoogle Scholar
Futer, D., Kalfagianni, E. and Purcell, J.. Guts of surfaces and the colored Jones polynomial. Lecture Notes in Math., 2069, (Springer, Heidelberg, 2013).Google Scholar
Geiges, H.. An introduction to contact topology . Camb. Stud. Adv. Math. 109. (Cambridge University Press, Cambridge, 2008).Google Scholar
Gordon, C. M. and Litherland, R. A.. On the signature of a link. Invent. Math. 47(1) (1978), 53–69.Google Scholar
Hayden, K. and Sabloff, J. M.. Positive knots and Lagrangian fillability. Proc. Amer. Math. Soc. 143(4) (2015), 1813–1821.CrossRefGoogle Scholar
Kálmán, T.. Maximal Thurston–Bennequin number of +adequate links. Proc. Amer. Math. Soc. 136(8) (2008), 2969–2977.Google Scholar
Kálmán, T.. Rulings of Legendrian knots as spanning surfaces. Pacific J. Math. 237(2) (2008), 287–297.Google Scholar
Lickorish, W. B. R. and Thistlethwaite, M. B.. Some links with nontrivial polynomials and their crossing-numbers. Comment. Math. Helv. 63(4) (1988), 527–539.Google Scholar
Lipman, E. R. and Sabloff, J. M.. Lagrangian fillings of Legendrian 4-plat knots. Geom. Ded. 198(1) (2019), 35–55.Google Scholar
Liu, Y. and Zhou, S.. Personal communication. (2017).Google Scholar
Massey, W. S.. Proof of a conjecture of Whitney. Pacific J. Math. 31(1) (1969), 143–156.Google Scholar
Melvin, P. and Shrestha, S.. The nonuniqueness of Chekanov polynomials of Legendrian knots. Geom. Topol. 9 (2005), 1221–1252.Google Scholar
Mishachev, K.. The n-copy of a topologically trivial Legendrian knot. J. Symplectic Geom. 1(4) (2003), 659–682.Google Scholar
Ng, L.. Invariants of Legendrian links. PhD. thesis. Massachusetts Institute of Technology (2001).Google Scholar
Ng, L.. A Legendrian Thurston–Bennequin bound from Khovanov homology. Algebr. Geom. Topol. 5 (2005), 1637–1653.Google Scholar
Ozsváth, P. S., Stipsicz, A. I. and Szabó, Z.. Unoriented knot Floer homology and the unoriented four-ball genus. Int. Math. Res. Not. (2017), no. 17, 5137–5181. MR3694597Google Scholar
Pan, Y.. The augmentation category map induced by exact Lagrangian cobordisms. Algebr. Geom. Topol. 17(3) (2017), 1813–1870.Google Scholar
Rutherford, D.. Thurston–Bennequin number, Kauffman polynomial, and ruling invariants of a Legendrian link: the Fuchs conjecture and beyond. Int. Math. Res. Not. (2006), art. ID 78591, 15.Google Scholar
Sabloff, J. M.. Augmentations and rulings of Legendrian knots. Int. Math. Res. Not. (2005), no. 19, 1157–1180.Google Scholar
Sabloff, J. M.. Ruling and augmentation invariants of Legendrian knots. Encyclopedia of Knot Theory (Allison Henrich Louis H. Kauffman Lewis D. Ludwig Sam Nelson Colin Adams, Erica Flapan, ed.) (CRC Press, 2021), pp. 403–410.Google Scholar
Sivek, S.. A bordered Chekanov–Eliashberg algebra. J. Topol. 4(1) (2011), 73–104.Google Scholar
Tagami, K.. On the Lagrangian fillability of almost positive links. J. Korean Math. Soc. 56(3) (2019), 789–804.Google Scholar
Tanaka, T.. Maximal Bennequin numbers and Kauffman polynomials of positive links. Proc. Amer. Math. Soc. 127(11) (1999), 3427–3432.Google Scholar
Traynor, L.. An introduction to the world of Legendrian and transverse knots. Encyclopedia of Knot Theory (Allison Henrich Louis H. Kauffman Lewis D. Ludwig Sam Nelson Colin Adams, Erica Flapan, ed.) (CRC Press, 2021), pp. 385–392.Google Scholar
Yokota, Y.. The Kauffman polynomial of periodic knots. Topology 32(2) (1993), 309–324.Google Scholar