Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-06-21T13:46:15.604Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear integral inequalities of the Volterra type

Published online by Cambridge University Press:  24 October 2008

Ryszard Szwarc
Ryszard Szwarc
Affiliation:
Department of Mathematics, University of Wisconsin-Madison, Madison, Wi 53706, U.S.A. Institute of Mathematics, Wroclaw University, pl. Grunwaldzki 2/4, 50–384 Wroclaw, Poland
Get access Rights & Permissions [Opens in a new window]

Extract

We are studying the integral inequality

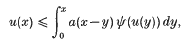
where all functions appearing are defined and increasing on the right half-axis and take the value zero at zero. We are interested in determining when the inequality admits solutions u(x) which are non-vanishing in a neighbourhood of zero. It is well-known that if ψ(x) is the identity function then no such solution exists. This due to the fact that the operator defined by the integral on the right-hand side of the equation is linear and compact. So if we are interested in non-trivial solutions it is natural to require that ψ(x) > 0 at least for all non-zero points in some neighbourhood of zero. One of the typical examples is the power function ψ(x) = xα, where α < 1. This situation was explored in [2]. The functions a(x) that admit non-zero solutions were characterized by Bushell in [1]. For a general approach to the problem we refer to [2], [3] and [4].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 111 , Issue 3 , May 1992 , pp. 599 - 608
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bushell, P. J.. On a class of Volterra and Fredholm non-linear integral equations. Math. Proc. Cambridge Philos. Soc. 79 (1979), 329–335.Google Scholar
[2]Bushell, P. J. and Okrasiński, W.. Uniqueness of solutions for a class of non-linear Volterra integral equations with convolution kernel. Math. Proc. Cambridge Philos. Soc. 106 (1989), 547–552.Google Scholar
[3]Okrasiński, W.. On a nonlinear Volterra equation. Math. Methods Appl. Sci. 8 (1986), 345–350.Google Scholar
[4]Szwarc, R.. Attraction principle for nonlinear integral operators of the Volterra type. J. Math. Anal. Appl., to appear.Google Scholar