Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-20T03:00:56.045Z Has data issue: false hasContentIssue false
  • English
  • Français

A new method for generating Bonferroni-type inequalities by iteration

Published online by Cambridge University Press:  24 October 2008

Janos Galambos  and
Yuan Xu
Janos Galambos
Affiliation:
Department of Mathematics, TU 038-16, Temple University, Philadelphia, PA 19122, U.S.A.
Yuan Xu
Affiliation:
Department of Mathematics, University of Texas at Austin, Austin, Texas 78712, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let A1,A2,…,An be events on a given probability space, and let mn be the number of those Aj which occur. Put S0 = S0,n = 1, and

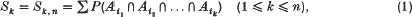
where the summation is over all subscripts satisfying 1 ≤ i1 < i2 < … < ik ≤ n. For convenience in some formulae we adopt the convention Sk, n = 0 if k > n. By turning to indicator variables one immediately finds that

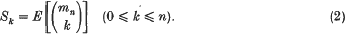
Inequalities of the form

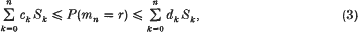
where ck = ck(r, n) and dk = dk(r, n) are constants (not dependent on the events Aj, 1 ≤ j ≤ n), possibly zero, are called Bonferroni-type inequalities. This same name applies if P(mn = r) is replaced by P(mn ≥ r) in the middle. The best known such inequalities are the method of inclusion and exclusion

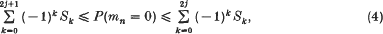
where j ≥ 0 is an arbitrary integer. An extension of (4) to arbitrary r, called Jordan's inequalities (see Takács [16]), is as follows: for 0 ≤ r ≤ n and for any integer j ≥ 0,

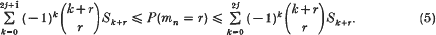
It is observed by Galambos and Mucci[9] that (5) follows from (4), and indeed, one can always generate inequalities of the form (3) for arbitrary r from the special case r = 0 if one utilizes only Sr,Sr+1… in the case of P(mn = r). As a matter of fact, from the instructions of Galambos and Mucci one has that the inequalities

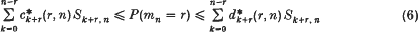
hold for an arbitrary sequence A1,A2,…,An of events if, and only if, for an arbitrary sequence A1,A2,…,An−r of events,

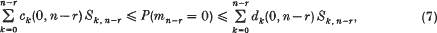
where

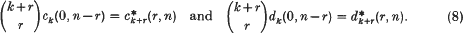
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 107 , Issue 3 , May 1990 , pp. 601 - 607
Copyright
Copyright © Cambridge Philosophical Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chung, K. L.. Elementary Probability Theory with Stochastic Processes (Springer-Verlag, 1974).CrossRefGoogle Scholar
[2]David, F. N. and Barton, D. E.. Combinatorial Chance (Griffin, 1962).CrossRefGoogle Scholar
[3]Dawson, D. A. and Sankoff, D.. An inequality for probabilities. Proc. Amer. Math. Soc. 18 (1967), 504–507.CrossRefGoogle Scholar
[4]de Koninck, J.-M. and Galambos, J.. The intermediate prime divisors of integers. Proc. Amer. Math. Soc. 101 (1987), 213–216.CrossRefGoogle Scholar
[5]Feller, W.. An Introduction to Probability Theory and its Applications, vol. 1. 2nd ed. (Wiley, 1957).Google Scholar
[6]Galambos, J.. Methods for proving Bonferroni type inequalities. J. London Math. Soc. (2) 9 (1975), 561–564.CrossRefGoogle Scholar
[7]Galambos, J.. Bonferroni inequalities. Ann. Probab. 5 (1977), 577–581.CrossRefGoogle Scholar
[8]Galambos, J.. The Asymptotic Theory of Extreme Order Statistics, 2nd edition (Krieger, 1987).Google Scholar
[9]Galambos, J. and Mucci, R.. Inequalities for linear combinations of binomial moments. Publ. Math. Debrecen 27 (1980), 263–268.CrossRefGoogle Scholar
[10]Hoppe, F. M.. Iterating Bonferroni bounds. Statist. Probab. Lett. 3 (1985), 121–125.CrossRefGoogle Scholar
[11]Kwerel, S. M.. Most stringent bounds on aggregated probabilities of partially specified dependent systems. J. Amer. Statist. Assoc. 70 (1975), 472–479.CrossRefGoogle Scholar
[12]Kwerel, S. M.. Bounds on the probability of the union and intersection of to events. Adv. in Appl. Probab. 7 (1975), 431–438.CrossRefGoogle Scholar
[13]Prékopa, A.. Boole–Bonferroni inequalities and linear programming. Oper. Res. 36 (1988), 145–162.CrossRefGoogle Scholar
[14]Seneta, E.. Degree, iteration and permutation in improving Bonferroni-type bounds. Austral. J. Statist. 30A (1988), 27–38.CrossRefGoogle Scholar
[15]Sobel, M. and Uppuluri, V. R. R.. On Bonferroni-type inequalities of the same degree for the probability of unions and intersections. Ann. Math. Statist. 43 (1972), 1549–1558.CrossRefGoogle Scholar
[16]Takács, L.. On a general probability theorem and its applications in the theory of stochastic processes. Proc. Cambridge Philos. Soc. 54 (1958), 219–224.CrossRefGoogle Scholar
[17]Tan, X. and Xu, Y.. Some inequalities of Bonferroni–Galambos type. Statist. Probab. Lett. 8 (1989), 17–20.CrossRefGoogle Scholar
[18]Xu, Y.. Bonferroni-type inequalities via interpolating polynomials. Proc. Amer. Math. Soc. 107 (1989), 825–831.CrossRefGoogle Scholar