Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Järvenpää, Maarit
2017.
Recent Developments in Fractals and Related Fields.
p.
175.
Järvenpää, Esa
Järvenpää, Maarit
Koivusalo, Henna
Li, Bing
Suomala, Ville
and
Xiao, Yimin
2017.
Hitting probabilities of random covering sets in tori and metric spaces.
Electronic Journal of Probability,
Vol. 22,
Issue. none,
Allen, Demi
and
Beresnevich, Victor
2018.
A mass transference principle for systems of linear forms and its applications.
Compositio Mathematica,
Vol. 154,
Issue. 5,
p.
1014.
HUSSAIN, MUMTAZ
and
WANG, WEILIANG
2018.
TWO-DIMENSIONAL SHRINKING TARGET PROBLEM IN BETA-DYNAMICAL SYSTEMS.
Bulletin of the Australian Mathematical Society,
Vol. 97,
Issue. 1,
p.
33.
Allen, Demi
and
Baker, Simon
2019.
A general mass transference principle.
Selecta Mathematica,
Vol. 25,
Issue. 3,
MA, CHAO
and
ZHANG, SHAOHUA
2019.
JARNÍK’S THEOREM WITHOUT THE MONOTONICITY ON THE APPROXIMATING FUNCTION.
Fractals,
Vol. 27,
Issue. 04,
p.
1950044.
WANG, WEILIANG
and
LI, LU
2020.
SIMULTANEOUS DYNAMICAL DIOPHANTINE APPROXIMATION IN BETA EXPANSIONS.
Bulletin of the Australian Mathematical Society,
Vol. 102,
Issue. 2,
p.
186.
Zhong, Wenmin
2021.
Mass Transference Principle: From balls to arbitrary shapes: Measure theory.
Journal of Mathematical Analysis and Applications,
Vol. 495,
Issue. 1,
p.
124691.
Wang, Baowei
and
Wu, Jun
2021.
Mass transference principle from rectangles to rectangles in Diophantine approximation.
Mathematische Annalen,
Vol. 381,
Issue. 1-2,
p.
243.
Hussain, Mumtaz
2021.
2019-20 MATRIX Annals.
Vol. 4,
Issue. ,
p.
175.
DING, NAN
2021.
LARGE INTERSECTION PROPERTIES FOR LIMSUP SETS GENERATED BY RECTANGLES IN COMPACT METRIC SPACES.
Fractals,
Vol. 29,
Issue. 06,
p.
2150137.
Beresnevich, Victor
Levesley, Jason
and
Ward, Ben
2021.
A lower bound for the Hausdorff dimension of the set of weighted simultaneously approximable points over manifolds.
International Journal of Number Theory,
Vol. 17,
Issue. 08,
p.
1795.
Chen, Changhao
and
Shparlinski, Igor E.
2021.
Small values of Weyl sums.
Journal of Mathematical Analysis and Applications,
Vol. 495,
Issue. 2,
p.
124743.
Koivusalo, Henna
and
Rams, Michał
2021.
Mass Transference Principle: From Balls to Arbitrary Shapes.
International Mathematics Research Notices,
Vol. 2021,
Issue. 8,
p.
6315.
Eceizabarrena, Daniel
and
Ponce-Vanegas, Felipe
2022.
Pointwise convergence over fractals for dispersive equations with homogeneous symbol.
Journal of Mathematical Analysis and Applications,
Vol. 515,
Issue. 1,
p.
126385.
Wang, Weiliang
Li, Lu
Wang, Xiujian
and
Yue, Qin
2022.
Doubly metric theory and simultaneous shrinking target problem in Cantor series expansion.
International Journal of Number Theory,
Vol. 18,
Issue. 08,
p.
1807.
BERESNEVICH, V.
LEVESLEY, J.
and
WARD, B.
2023.
Simultaneous p-adic Diophantine approximation.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 175,
Issue. 1,
p.
13.
Chen, Changhao
Kerr, Bryce
Maynard, James
and
Shparlinski, Igor E.
2023.
Metric theory of Weyl sums.
Mathematische Annalen,
Vol. 385,
Issue. 1-2,
p.
309.
Beresnevich, Victor
and
Velani, Sanju
2023.
The divergence Borel–Cantelli Lemma revisited.
Journal of Mathematical Analysis and Applications,
Vol. 519,
Issue. 1,
p.
126750.
Kleinbock, Dmitry
and
Wang, Baowei
2023.
Measure theoretic laws for limsup sets defined by rectangles.
Advances in Mathematics,
Vol. 428,
Issue. ,
p.
109154.
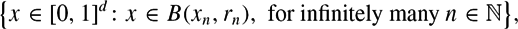 \begin{equation*}\big\{x\in [0,1]^d: x\in B(x_n,r_n), \ {{\rm for}\, {\rm infinitely}\, {\rm many}}\ n\in \mathbb{N}\big\},\end{equation*}
\begin{equation*}\big\{x\in [0,1]^d: x\in B(x_n,r_n), \ {{\rm for}\, {\rm infinitely}\, {\rm many}}\ n\in \mathbb{N}\big\},\end{equation*}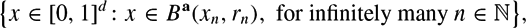 \begin{equation*}\big\{x\in [0,1]^d: x\in B^{a}(x_n,r_n), \ {{\rm for}\, {\rm infinitely}\, {\rm many}}\ n\in \mathbb{N}\big\},\end{equation*}
\begin{equation*}\big\{x\in [0,1]^d: x\in B^{a}(x_n,r_n), \ {{\rm for}\, {\rm infinitely}\, {\rm many}}\ n\in \mathbb{N}\big\},\end{equation*}



