Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-10T08:29:19.163Z Has data issue: false hasContentIssue false
  • English
  • Français

The Markov branching process with density-independent catastrophes. II. The subcritical and critical cases

Published online by Cambridge University Press:  28 June 2011

Anthony G. Pakes
Anthony G. Pakes
Affiliation:
Department of Mathematics, University of Western Australia, Nedlands, WA 6009, Australia
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper continues the study initiated in [10] of the Markov branching process (MBP) subject to an independent Poisson process of catastrophe times at which the population size is reduced by random decrements whose distribution is independent of the current population size. More generally, let (Xt:t ≥ 0) be the Feller process on the non-negative integers ℕ+ having the generator

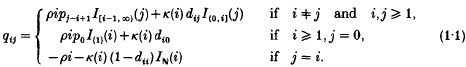
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 106 , Issue 2 , September 1989 , pp. 369 - 383
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Athreya, K. B. and Ney, P. E.. Branching Processes (Springer-Verlag, 1972).CrossRefGoogle Scholar
[2] Bingham, N. H., Goldie, C. M. and Teugels, J. L.. Regular Variation (Cambridge University Press, 1987).CrossRefGoogle Scholar
[3] Brockwell, P. J.. The extinction time of a birth, death and catastrophe process and of a related diffusion model. Adv. in Appl. Probab. 17 (1985), 42–52.CrossRefGoogle Scholar
[4] Brockwell, P. J., Gani, J. and Resnick, S. I.. Birth, immigration and catastrophe processes. Adv. in Appl. Probab. 14 (1982), 709–731.CrossRefGoogle Scholar
[5] Ewens, W. J., Brockwell, P. J., Gani, J. and Resnick, S. I.. Minimum viable population size in the presence of catastrophes. In Soulé, M. (ed.) Viable Populations for Conservation (Cambridge University Press, 1987), pp. 59–68.CrossRefGoogle Scholar
[6] Grey, D. R.. Supercritical branching processes with density independent catastrophes. Math. Proc. Cambridge Philos. Soc. 104 (1988), 413–416.CrossRefGoogle Scholar
[7] Hanson, F. B. and Tuckwell, H. C.. Persistence times of populations with large random fluctuations. Theoret. Population Biol. 14 (1978), 46–61.CrossRefGoogle ScholarPubMed
[8] Pakes, A. G.. The Markov branching-catastrophe process. Stochastic Process. Appl. 23 (1986), 1–33.CrossRefGoogle Scholar
[9] Pakes, A. G.. Limit theorems for the population size of a birth and death process allowing catastrophes. J. Math. Biol. 25 (1987), 307–325.CrossRefGoogle ScholarPubMed
[10] Pakes, A. G.. The Markov branching process with density-independent catastrophes. I. Behaviour of extinction probabilities. Math. Proc. Cambridge Philos. Soc. 103 (1988), 351–366.CrossRefGoogle Scholar
[11] Pakes, A. G.. The supercritical birth, death and catastrophe process: Limit theorems on the set of non-extinction. J. Math. Biol. 26 (1986), 405–420.CrossRefGoogle Scholar
[12] Pakes, A. G.. Asymptotic results for the extinction time of Markov branching processes allowing emigration, I. Random walk decrements. Adv. in Appl. Probab. (to appear).Google Scholar
[13] Pakes, A. G.. The Markov branching process with density-independent catastrophes. III. the supercritical case. Math. Proc. Cambridge Philos. Soc. 107 (1980) (to appear).Google Scholar
[14] Pakes, A. G. and Pollett, P.. The supercritical birth, death and catastrophe process: Limit theorems on the set of extinction. Stochastic Process Appl. (to appear).Google Scholar
[15] Stoyan, D.. Comparison Methods for Queues and other Stochastic Models (J. Wiley, 1983).Google Scholar