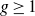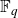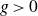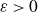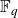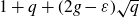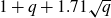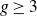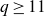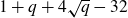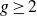1. Introduction
Researchers who study
![]() $N_q(g)$
, the maximal number of rational points on curvesFootnote
1
of genus g over a finite field
$N_q(g)$
, the maximal number of rational points on curvesFootnote
1
of genus g over a finite field
![]() $\mathbb{F}_q$
, generally follow the lead of Serre’s 1985 Harvard lectures [
Reference SerreSer20
] and focus on two cases: one in which q is fixed and the genus goes to infinity, and one in which g is fixed and q varies. In the first case, a great number of results have been achieved that control the asymptotic behaviour of the ratio
$\mathbb{F}_q$
, generally follow the lead of Serre’s 1985 Harvard lectures [
Reference SerreSer20
] and focus on two cases: one in which q is fixed and the genus goes to infinity, and one in which g is fixed and q varies. In the first case, a great number of results have been achieved that control the asymptotic behaviour of the ratio
![]() $N_q(g)/g$
; see [
Reference BeelenBee22
] and the references there. In the second case, while a closed formula is known for
$N_q(g)/g$
; see [
Reference BeelenBee22
] and the references there. In the second case, while a closed formula is known for
![]() $N_q(0), N_q(1)$
[
Reference DeuringDeu41
] and
$N_q(0), N_q(1)$
[
Reference DeuringDeu41
] and
![]() $N_q(2)$
[
Reference SerreSer83
], the exact nature of the growth of
$N_q(2)$
[
Reference SerreSer83
], the exact nature of the growth of
![]() $N_q(g)$
for fixed q remains open in general. One of the tantalising challenges already proposed in [
Reference SerreSer20
, section 4·3] is to determine whether for every g, the value
$N_q(g)$
for fixed q remains open in general. One of the tantalising challenges already proposed in [
Reference SerreSer20
, section 4·3] is to determine whether for every g, the value
![]() $N_q(g)$
remains at a bounded distance from the Hasse–Weil bound
$N_q(g)$
remains at a bounded distance from the Hasse–Weil bound
![]() $1+q+2g\sqrt{q}$
for all q, as is the case for
$1+q+2g\sqrt{q}$
for all q, as is the case for
![]() $g=0, 1$
and 2. It is hard even to get good heuristics for this question (see our attempt in Remark 2·5), and in a recent personal communication J-P. Serre raised a less ambitious question: is it possible to give for each g a positive constant c such that for all sufficiently large q, we have
$g=0, 1$
and 2. It is hard even to get good heuristics for this question (see our attempt in Remark 2·5), and in a recent personal communication J-P. Serre raised a less ambitious question: is it possible to give for each g a positive constant c such that for all sufficiently large q, we have
![]() $N_q(g)\ge 1+q +c \sqrt{q}$
? In this paper we provide several methods that lead to a positive answer to the question, even when we limit our consideration to hyperelliptic curves.
$N_q(g)\ge 1+q +c \sqrt{q}$
? In this paper we provide several methods that lead to a positive answer to the question, even when we limit our consideration to hyperelliptic curves.
Serre not only asked this question but also suggested that it might be answered through the consideration of the (weighted) sum
![]() $S_n(q,\mathcal{H}_g)$
of the nth powers of the traces of Frobenius of genus-g hyperelliptic curves over
$S_n(q,\mathcal{H}_g)$
of the nth powers of the traces of Frobenius of genus-g hyperelliptic curves over
![]() $\mathbb{F}_q$
, for even n. This strategy is at the root of the computations we present in Section 3, which is chronologically the first path we followed. Using the explicit formula from [
Reference BergströmBer09
] for
$\mathbb{F}_q$
, for even n. This strategy is at the root of the computations we present in Section 3, which is chronologically the first path we followed. Using the explicit formula from [
Reference BergströmBer09
] for
![]() $n=6$
, one finds for instance that for
$n=6$
, one finds for instance that for
![]() $g \geq 3$
and
$g \geq 3$
and
![]() $q \geq 25$
, we have
$q \geq 25$
, we have
![]() $N_q(g) \geq 1+q+1.55 \sqrt{q}$
.
$N_q(g) \geq 1+q+1.55 \sqrt{q}$
.
We then quickly realised that by using Katz–Sarnak theory, one can actually get an optimal result of this flavor, namely that for every
![]() $\varepsilon>0$
and every g, there exists a
$\varepsilon>0$
and every g, there exists a
![]() $q_0$
such that for
$q_0$
such that for
![]() $q>q_0$
, one has
$q>q_0$
, one has
![]() $N_q(g) \geq 1+q+(2g-\varepsilon) \sqrt{q}$
(see Corollary 2·3). We were surprised to find no trace of this result in the existing literature, as it can be derived easily. Notice though that a related result appears already in [
Reference SerreSer20
, remark 1·1·2]: For every curve
$N_q(g) \geq 1+q+(2g-\varepsilon) \sqrt{q}$
(see Corollary 2·3). We were surprised to find no trace of this result in the existing literature, as it can be derived easily. Notice though that a related result appears already in [
Reference SerreSer20
, remark 1·1·2]: For every curve
![]() $C/\mathbb{F}_q$
and
$C/\mathbb{F}_q$
and
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
![]() $\lvert\#C(\mathbb{F}_{q^i}) - (q^i+1)\rvert \ge (2g-\varepsilon) \sqrt{q^i}$
for infinitely many i.
$\lvert\#C(\mathbb{F}_{q^i}) - (q^i+1)\rvert \ge (2g-\varepsilon) \sqrt{q^i}$
for infinitely many i.
One drawback of the method used in Section 2 in comparison with the one in Section 3 is of course that the value of
![]() $q_0$
is unknown. It is then tempting to push the method of Section 3 using
$q_0$
is unknown. It is then tempting to push the method of Section 3 using
![]() $S_n(q,\mathcal{H}_g)$
further on, in particular since one shows in Theorem 3·9 that the limit when n goes to infinity of
$S_n(q,\mathcal{H}_g)$
further on, in particular since one shows in Theorem 3·9 that the limit when n goes to infinity of
 \[\mathfrak{a}_{2n}(g)\;:\!=\; \left(\lim_{q \to \infty} \frac{S_{2n}(q,\mathcal{H}_g)}{q^{2g-1+n/2}}\right)^{\frac{1}{2n}}\]
\[\mathfrak{a}_{2n}(g)\;:\!=\; \left(\lim_{q \to \infty} \frac{S_{2n}(q,\mathcal{H}_g)}{q^{2g-1+n/2}}\right)^{\frac{1}{2n}}\]
is 2g. This proves that the strategy using moments provides the same asymptotic bound as Katz–Sarnak. But the lack of an explicit formula for
![]() $S_{2n}(q,\mathcal{H}_g)$
when n is large also prevents us from giving an explicit value for
$S_{2n}(q,\mathcal{H}_g)$
when n is large also prevents us from giving an explicit value for
![]() $q_0$
. Interestingly though, one can show that
$q_0$
. Interestingly though, one can show that
![]() $\mathfrak{a}_{2n}(g)$
can also be efficiently computed using a representation of
$\mathfrak{a}_{2n}(g)$
can also be efficiently computed using a representation of
![]() $\textrm{USp}_{2g}$
; see Theorem 3·8.
$\textrm{USp}_{2g}$
; see Theorem 3·8.
In Section 4 we develop yet another approach, which surpasses our best lower bounds from Section 3: we show that under relatively mild hypotheses, a hyperelliptic curve C of genus g can be covered by hyperelliptic curves of genus 2g and
![]() $2g+1$
that have at least as many rational points as does C. By starting with well-chosen hyperelliptic curves of genus 2 and 3 with at least
$2g+1$
that have at least as many rational points as does C. By starting with well-chosen hyperelliptic curves of genus 2 and 3 with at least
![]() $1+q + 4\sqrt{q} - 32$
points, we can recursively construct a hyperelliptic curve of any desired genus that has at least this many rational points. This lower bound is obviously smaller than the one we obtain using the Katz–Sarnak approach, but it is better than the one we find using the first few values of
$1+q + 4\sqrt{q} - 32$
points, we can recursively construct a hyperelliptic curve of any desired genus that has at least this many rational points. This lower bound is obviously smaller than the one we obtain using the Katz–Sarnak approach, but it is better than the one we find using the first few values of
![]() $S_n(q,\mathcal{H}_g)$
, and it applies to all q. The method also suggests an algorithm for producing an explicit curve of any given genus that surpasses this lower bound; see Section 4.3.
$S_n(q,\mathcal{H}_g)$
, and it applies to all q. The method also suggests an algorithm for producing an explicit curve of any given genus that surpasses this lower bound; see Section 4.3.
2. Lower bounds from Katz–Sarnak distribution
For
![]() $g \geq 2$
, let
$g \geq 2$
, let
![]() $\mathcal{M}_g$
denote the (coarse) moduli space of smooth projective genus-g curves, and let
$\mathcal{M}_g$
denote the (coarse) moduli space of smooth projective genus-g curves, and let
![]() $\mathcal{H}_g$
denote the subspace of hyperelliptic curves. Note that
$\mathcal{H}_g$
denote the subspace of hyperelliptic curves. Note that
![]() $\mathcal{M}_g(\mathbb{F}_q)$
and
$\mathcal{M}_g(\mathbb{F}_q)$
and
![]() $\mathcal{H}_g(\mathbb{F}_q)$
consist of
$\mathcal{H}_g(\mathbb{F}_q)$
consist of
![]() $\overline{\mathbb{F}}_q$
-isomorphism classes of curves that have models over
$\overline{\mathbb{F}}_q$
-isomorphism classes of curves that have models over
![]() $\mathbb{F}_q$
. Let
$\mathbb{F}_q$
. Let
![]() $\mathcal{M}'_{\!\!g}(\mathbb{F}_q)$
and
$\mathcal{M}'_{\!\!g}(\mathbb{F}_q)$
and
![]() $\mathcal{H}'_{\!\!g}(\mathbb{F}_q)$
denote the sets of
$\mathcal{H}'_{\!\!g}(\mathbb{F}_q)$
denote the sets of
![]() $\mathbb{F}_q$
-isomorphism classes of (the appropriate types of) curves over
$\mathbb{F}_q$
-isomorphism classes of (the appropriate types of) curves over
![]() $\mathbb{F}_q$
.
$\mathbb{F}_q$
.
Theorem 2·1 (Katz–Sarnak, [
Reference Katz and SarnakKS99
, theorems 10·7·12 and 10·8·2]). Fix
![]() $g\geq 2$
. Let m be the Haar measure on
$g\geq 2$
. Let m be the Haar measure on
![]() $\textrm{USp}_{2g}$
, the compact symplectic group. If f is a continuous function on
$\textrm{USp}_{2g}$
, the compact symplectic group. If f is a continuous function on
![]() $\textrm{USp}_{2g}$
that is constant on the conjugacy classes, then
$\textrm{USp}_{2g}$
that is constant on the conjugacy classes, then
 \begin{align*}\int_{m \in \textrm{USp}_{2g}} f(m) \,dm& = \int_{\theta \in [0,\pi]^g} f \circ h(\theta) \,d\mu_g(\theta) \\[5pt] & = \frac{1}{\# \mathcal{M}_g(\mathbb{F}_q)} \cdot \sum_{C \in \mathcal{M}'_{\!\!g}(\mathbb{F}_q)} \frac{f\circ h(\theta_C)}{\# \textrm{Aut}_{\mathbb{F}_q}(C)} +O(q^{-1/2})\,,\end{align*}
\begin{align*}\int_{m \in \textrm{USp}_{2g}} f(m) \,dm& = \int_{\theta \in [0,\pi]^g} f \circ h(\theta) \,d\mu_g(\theta) \\[5pt] & = \frac{1}{\# \mathcal{M}_g(\mathbb{F}_q)} \cdot \sum_{C \in \mathcal{M}'_{\!\!g}(\mathbb{F}_q)} \frac{f\circ h(\theta_C)}{\# \textrm{Aut}_{\mathbb{F}_q}(C)} +O(q^{-1/2})\,,\end{align*}
where
![]() $\theta_C=(\theta_1,\ldots,\theta_g) \in [0,\pi]^g$
are the Frobenius angles of the Jacobian of C, where h is the function given by
$\theta_C=(\theta_1,\ldots,\theta_g) \in [0,\pi]^g$
are the Frobenius angles of the Jacobian of C, where h is the function given by
and where
![]() $d\mu_g(\theta) = \delta_g(\theta) \,d\theta_1\cdots d\theta_g$
is the density measure with
$d\mu_g(\theta) = \delta_g(\theta) \,d\theta_1\cdots d\theta_g$
is the density measure with
The same holds when one replaces
![]() $\mathcal{M}_g$
with
$\mathcal{M}_g$
with
![]() $\mathcal{H}_g$
.
$\mathcal{H}_g$
.
As a consequence of Theorem 2·1, we obtain the following result. For
![]() $\mathcal{M}_g$
this is [
Reference LachaudLac16
, corollary 4·3]; the proof for
$\mathcal{M}_g$
this is [
Reference LachaudLac16
, corollary 4·3]; the proof for
![]() $\mathcal{H}_g$
follows the same argument presented in [
Reference LachaudLac16
].
$\mathcal{H}_g$
follows the same argument presented in [
Reference LachaudLac16
].
Proposition 2·2.
Fix
![]() $g\geq 2$
. For a genus-g curve we write
$g\geq 2$
. For a genus-g curve we write
![]() $\#C(\mathbb{F}_q)=1+q+\tau(C)\sqrt{q}$
. Then we have
$\#C(\mathbb{F}_q)=1+q+\tau(C)\sqrt{q}$
. Then we have
where
![]() $F(x)=\int_{A_x} d\mu_g$
and
$F(x)=\int_{A_x} d\mu_g$
and
![]() $A_x=\{(\theta_1,...,\theta_g)\in[0,\pi]^g:\,\sum_{j}2\operatorname{cos}\theta_j\leq x\}$
. The same holds when one replaces
$A_x=\{(\theta_1,...,\theta_g)\in[0,\pi]^g:\,\sum_{j}2\operatorname{cos}\theta_j\leq x\}$
. The same holds when one replaces
![]() $\mathcal{M}_g$
with
$\mathcal{M}_g$
with
![]() $\mathcal{H}_g$
.
$\mathcal{H}_g$
.
Corollary 2·3.
Fix
![]() $g\geq 2$
and
$g\geq 2$
and
![]() $\varepsilon>0$
. For all sufficiently large q, there exist hyperelliptic genus-g curves
$\varepsilon>0$
. For all sufficiently large q, there exist hyperelliptic genus-g curves
![]() $C/\mathbb{F}_q$
and
$C/\mathbb{F}_q$
and
![]() $C'/\mathbb{F}_q$
with
$C'/\mathbb{F}_q$
with
![]() $\#C(\mathbb{F}_q)\geq1+q+(2g-\varepsilon)\sqrt{q}$
and
$\#C(\mathbb{F}_q)\geq1+q+(2g-\varepsilon)\sqrt{q}$
and
![]() $\#C'(\mathbb{F}_q)\leq 1+q-(2g-\varepsilon)\sqrt{q}$
.
$\#C'(\mathbb{F}_q)\leq 1+q-(2g-\varepsilon)\sqrt{q}$
.
Proof. Applying Proposition 2·2 to
![]() $\mathcal{H}_g$
, we find that for q large enough there exists
$\mathcal{H}_g$
, we find that for q large enough there exists
![]() $c>0$
such that
$c>0$
such that
Since
![]() $F\colon\mathbb{R}\rightarrow[0,1]$
does not depend on q and is a continuous, non-negative, strictly increasing function on
$F\colon\mathbb{R}\rightarrow[0,1]$
does not depend on q and is a continuous, non-negative, strictly increasing function on
![]() $[\!-\!2g,2g]$
with
$[\!-\!2g,2g]$
with
![]() $F(2g)=1$
, we have also, for q large enough,
$F(2g)=1$
, we have also, for q large enough,
Hence,
Since
![]() $\#\mathcal{H}_g(\mathbb{F}_q)=q^{2g-1}$
[
Reference Brock and GranvilleBG01
, proposition 7·1, p. 87], multiplying the previous inequality by this cardinality, we see that there exists a hyperelliptic curve
$\#\mathcal{H}_g(\mathbb{F}_q)=q^{2g-1}$
[
Reference Brock and GranvilleBG01
, proposition 7·1, p. 87], multiplying the previous inequality by this cardinality, we see that there exists a hyperelliptic curve
![]() $C/\mathbb{F}_q$
with
$C/\mathbb{F}_q$
with
![]() $\#C(\mathbb{F}_q)\geq1+q+(2g-\varepsilon)\sqrt{q}$
points. Taking its quadratic twist C
′ gives the other inequality.
$\#C(\mathbb{F}_q)\geq1+q+(2g-\varepsilon)\sqrt{q}$
points. Taking its quadratic twist C
′ gives the other inequality.
Remark 2·4. Actually, the theory of Katz–Sarnak (in particular [
Reference Katz and SarnakKS99
, 9·6·10]) allows us to prove a similar result for low-dimensional families of curves. For a given prime
![]() $\ell$
, let S be a connected normal scheme, separated and of finite type over
$\ell$
, let S be a connected normal scheme, separated and of finite type over
![]() $\mathbb{Z}[1/\ell]$
. Let
$\mathbb{Z}[1/\ell]$
. Let
![]() $X/S$
be a smooth scheme such that for each finite field k of characteristic different from
$X/S$
be a smooth scheme such that for each finite field k of characteristic different from
![]() $\ell$
and each point
$\ell$
and each point
![]() $s \in S(k)$
,
$s \in S(k)$
,
![]() $X_s/k$
is a curve of genus g. We assume that for each
$X_s/k$
is a curve of genus g. We assume that for each
![]() $X_s$
the geometric monodromy group satisfies [
Reference Katz and SarnakKS99
, 9·3·7·2]; in particular, it is conjugate in
$X_s$
the geometric monodromy group satisfies [
Reference Katz and SarnakKS99
, 9·3·7·2]; in particular, it is conjugate in
![]() $\textrm{GL}_{2g}$
to a constant group. Examples of such families include for instance the generic element of the one-parameter families
$\textrm{GL}_{2g}$
to a constant group. Examples of such families include for instance the generic element of the one-parameter families
![]() $y^2=f(x) (x-t)$
of hyperelliptic curves [
Reference HallHal08
] or cyclic triple covers of
$y^2=f(x) (x-t)$
of hyperelliptic curves [
Reference HallHal08
] or cyclic triple covers of
![]() $\mathbb{P}^1$
[
Reference Achter and PriesAP07
].
$\mathbb{P}^1$
[
Reference Achter and PriesAP07
].
Now we simply assume that the dimension of the image of
![]() $S \otimes \bar{k}$
in the moduli space is at least 1. Then there exists a function g(q) going to infinity such that
$S \otimes \bar{k}$
in the moduli space is at least 1. Then there exists a function g(q) going to infinity such that
![]() $\#S(\mathbb{F}_q) \geq g(q)$
. Moreover, Katz–Sarnak implies that for
$\#S(\mathbb{F}_q) \geq g(q)$
. Moreover, Katz–Sarnak implies that for
![]() $x \in [\!-\!2g,2g]$
we have
$x \in [\!-\!2g,2g]$
we have
for a strictly increasing distribution function F(x) and a decreasing function f(q) going to 0.
Given
![]() $\varepsilon>0$
, let q be large enough so that
$\varepsilon>0$
, let q be large enough so that
![]() $F(2g-\varepsilon)\leq 1-f(q)-\frac{1}{g(q)}$
. Then
$F(2g-\varepsilon)\leq 1-f(q)-\frac{1}{g(q)}$
. Then
which shows there is at least one curve in the family
![]() $X/S$
with more than
$X/S$
with more than
![]() $1+q+(2g-\varepsilon)\sqrt{q}$
points. More generally, this argument can be adapted to prove the existence of a curve with number of points in the interval
$1+q+(2g-\varepsilon)\sqrt{q}$
points. More generally, this argument can be adapted to prove the existence of a curve with number of points in the interval
![]() $[1+q+(a-\varepsilon)\sqrt{q},1+q+(a+\varepsilon)\sqrt{q}]$
for any a with
$[1+q+(a-\varepsilon)\sqrt{q},1+q+(a+\varepsilon)\sqrt{q}]$
for any a with
![]() $-2g \leq a \leq 2g$
.
$-2g \leq a \leq 2g$
.
Remark 2·5. The lower bound of Corollary 2·3 is of course far from answering Serre’s question on the existence of a curve with bounded defect. Even the question of the existence of infinitely many p for which there exist defect-0 curves of a fixed genus g over
![]() $\mathbb{F}_p$
is open. The following is a naive attempt to make up our mind on a direction to take for this challenge. The Jacobians of such curves are isogenous to powers of an ordinary elliptic curve
$\mathbb{F}_p$
is open. The following is a naive attempt to make up our mind on a direction to take for this challenge. The Jacobians of such curves are isogenous to powers of an ordinary elliptic curve
![]() $E/\mathbb{F}_p$
with trace
$E/\mathbb{F}_p$
with trace
![]() $-\lfloor 2 \sqrt{p} \rfloor $
. It is tempting to look at the number of principally polarized abelian varieties of this type up to isomorphism. Using the equivalence of categories [
Reference Kirschmer, Narbonne, Ritzenthaler and RobertKNRR21
, corollary 3·6], this is the same as counting, up to isometry, unimodular positive definite hermitian R-lattices of rank g where
$-\lfloor 2 \sqrt{p} \rfloor $
. It is tempting to look at the number of principally polarized abelian varieties of this type up to isomorphism. Using the equivalence of categories [
Reference Kirschmer, Narbonne, Ritzenthaler and RobertKNRR21
, corollary 3·6], this is the same as counting, up to isometry, unimodular positive definite hermitian R-lattices of rank g where
![]() $R=\mathbb{Z}[x]/(x^2+\lfloor 2 \sqrt{p} \rfloor x + p)$
. When R is maximal, crude estimations of the mass formulae and class numbers of [
Reference Ludwig SiegelSie35, Reference Ludwig SiegelSie37
] kindly provided by [
Reference KirschmerKir22
] show that their number should be smaller than
$R=\mathbb{Z}[x]/(x^2+\lfloor 2 \sqrt{p} \rfloor x + p)$
. When R is maximal, crude estimations of the mass formulae and class numbers of [
Reference Ludwig SiegelSie35, Reference Ludwig SiegelSie37
] kindly provided by [
Reference KirschmerKir22
] show that their number should be smaller than
![]() $C(g) \times \textrm{disc}(R)^{g(g+1)/4 + o(1)}$
, where C(g) is a constant that does not depend on R. Since
$C(g) \times \textrm{disc}(R)^{g(g+1)/4 + o(1)}$
, where C(g) is a constant that does not depend on R. Since
![]() $\textrm{disc}(R)$
is smaller than
$\textrm{disc}(R)$
is smaller than
![]() $4 \sqrt{p}$
, we get at most
$4 \sqrt{p}$
, we get at most
![]() $p^{g(g+1)/8 + o(1)}$
distinct principally polarized abelian varieties isogenous to the power of an elliptic curve with trace
$p^{g(g+1)/8 + o(1)}$
distinct principally polarized abelian varieties isogenous to the power of an elliptic curve with trace
![]() $-\lfloor 2 \sqrt{p} \rfloor $
. If one makes the assumption that Jacobians over
$-\lfloor 2 \sqrt{p} \rfloor $
. If one makes the assumption that Jacobians over
![]() $\mathbb{F}_p$
are well distributed among principally polarised abelian varieties over
$\mathbb{F}_p$
are well distributed among principally polarised abelian varieties over
![]() $\mathbb{F}_p$
, the ‘chance’ to fall in the Jacobian locus may be estimated as
$\mathbb{F}_p$
, the ‘chance’ to fall in the Jacobian locus may be estimated as
![]() $p^{(3g-3)-g(g+1)/2}$
. Hence for
$p^{(3g-3)-g(g+1)/2}$
. Hence for
![]() $g>6$
, it is heuristically unlikely to find a defect-0 curve over
$g>6$
, it is heuristically unlikely to find a defect-0 curve over
![]() $\mathbb{F}_p$
when p is large. We believe that the assumption that R be maximal is not necessary, but proving this would require a better understanding of the mass formulae for non-projective R-lattices.
$\mathbb{F}_p$
when p is large. We believe that the assumption that R be maximal is not necessary, but proving this would require a better understanding of the mass formulae for non-projective R-lattices.
3. Lower bound from explicit power of traces
3·1. Weighted trace powers
Let us define the correct moments we want to compute. If
![]() $C/\mathbb{F}_q$
is a genus-g curve, we denote by [C] the set of representatives of its twists and define
$C/\mathbb{F}_q$
is a genus-g curve, we denote by [C] the set of representatives of its twists and define
 \begin{equation} s_n(C) = \sum_{C' \in [C]} \frac{(q+1-\#C'(\mathbb{F}_q))^n}{\# \textrm{Aut}_{\mathbb{F}_q}(C')}\,.\end{equation}
\begin{equation} s_n(C) = \sum_{C' \in [C]} \frac{(q+1-\#C'(\mathbb{F}_q))^n}{\# \textrm{Aut}_{\mathbb{F}_q}(C')}\,.\end{equation}
The following result is probably well known, but we provide a proof for lack of proper reference (note that the case
![]() $s_0(C)=1$
can be found in [
Reference van der Geer and van der VlugtvdGvdV92
, proposition 5·1]).
$s_0(C)=1$
can be found in [
Reference van der Geer and van der VlugtvdGvdV92
, proposition 5·1]).
Proposition 3·1.
For every curve
![]() $C/\mathbb{F}_q$
and every
$C/\mathbb{F}_q$
and every
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $s_n(C)$
is an integer.
$s_n(C)$
is an integer.
For this, we will need some elementary lemmas. As in [
Reference Meagher and TopMT10
, proposition 9], let us define for
![]() $g\in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
, the set
$g\in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
, the set
![]() $[g]_{{Fr}}$
of elements h such that there exists
$[g]_{{Fr}}$
of elements h such that there exists
![]() $x\in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
with
$x\in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
with
![]() $h=xg\,^{{Fr}}\!x^{-1}$
, where
$h=xg\,^{{Fr}}\!x^{-1}$
, where
![]() $^{{Fr}}$
is the geometric
$^{{Fr}}$
is the geometric
![]() $\mathbb{F}_q$
-Frobenius morphism (acting here on
$\mathbb{F}_q$
-Frobenius morphism (acting here on
![]() $x^{-1}$
). To a given set
$x^{-1}$
). To a given set
![]() $[g]_{{Fr}}$
, one can associate a twist C
′ of C.
$[g]_{{Fr}}$
, one can associate a twist C
′ of C.
Lemma 3·2 ([
Reference van der Geer and van der VlugtvdGvdV92
, proof of proposition 5·1]). Let
![]() $g\in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
and let C’ be the twist associated to the Frobenius conjugacy class
$g\in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
and let C’ be the twist associated to the Frobenius conjugacy class
![]() $[g]_{{Fr}}$
of g. Then
$[g]_{{Fr}}$
of g. Then
![]() $\#\textrm{Aut}_{{\mathbb{F}_q}}(C')\cdot \#[g]_{{Fr}}=\#\textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
.
$\#\textrm{Aut}_{{\mathbb{F}_q}}(C')\cdot \#[g]_{{Fr}}=\#\textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
.
Lemma 3·3.
Let K be a field of characteristic 0, let n and k be positive integers and let G be a finite subgroup of
![]() $\textrm{GL}_k(K)$
.
$\textrm{GL}_k(K)$
.
-
(i) For every
 $A,B\in M_n(K)$
we have
$A,B\in M_n(K)$
we have
 $(A\cdot B)^{\otimes k}=A^{\otimes k}\cdot B^{\otimes k}$
.
$(A\cdot B)^{\otimes k}=A^{\otimes k}\cdot B^{\otimes k}$
. -
(ii) Hence, the map
 $g \mapsto g^{\otimes n}$
from G to
$g \mapsto g^{\otimes n}$
from G to
 $G^{\otimes n} \subseteq \textrm{GL}_{kn}(K)$
induces a surjective morphism on its image
$G^{\otimes n} \subseteq \textrm{GL}_{kn}(K)$
induces a surjective morphism on its image
 $G_n$
.
$G_n$
. -
(iii) The matrix
 $P_{G_n}=({1}/{\#G})\sum_{g\in G}g^{\otimes n}= ({1}/{\#G_n})\sum_{g\in G_n} g$
is a projection. Hence its eigenvalues are 0 and 1.
$P_{G_n}=({1}/{\#G})\sum_{g\in G}g^{\otimes n}= ({1}/{\#G_n})\sum_{g\in G_n} g$
is a projection. Hence its eigenvalues are 0 and 1.
By abuse of notation we denote by
![]() $g\in\textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
the corresponding element in
$g\in\textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
the corresponding element in
![]() $\textrm{Aut}_{\overline{\mathbb{F}}_q}(T_{\ell} \textrm{Jac} C)$
that we see as a matrix of size
$\textrm{Aut}_{\overline{\mathbb{F}}_q}(T_{\ell} \textrm{Jac} C)$
that we see as a matrix of size
![]() $2g\times 2g$
with coefficients in
$2g\times 2g$
with coefficients in
![]() $\mathbb{Z}_{\ell}$
for a prime
$\mathbb{Z}_{\ell}$
for a prime
![]() $\ell\neq p$
. We fix an embedding
$\ell\neq p$
. We fix an embedding
![]() $\mathbb{Z}_{\ell}\hookrightarrow\mathbb{C}$
of
$\mathbb{Z}_{\ell}\hookrightarrow\mathbb{C}$
of
![]() $\mathbb{Z}_{\ell}$
into the complex numbers. Let
$\mathbb{Z}_{\ell}$
into the complex numbers. Let
![]() $\pi_C$
denote the Frobenius endomorphism of
$\pi_C$
denote the Frobenius endomorphism of
![]() $\textrm{Jac} C$
or its matrix for the action on
$\textrm{Jac} C$
or its matrix for the action on
![]() $T_{\ell} \textrm{Jac} C$
in some arbitrary basis. Let us recall from [
Reference Meagher and TopMT10
, proposition 11] that if C
′ is a twist of C given by an element
$T_{\ell} \textrm{Jac} C$
in some arbitrary basis. Let us recall from [
Reference Meagher and TopMT10
, proposition 11] that if C
′ is a twist of C given by an element
![]() $g\in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
then
$g\in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
then
![]() $\pi_{C'}=\pi_{C} \cdot g$
.
$\pi_{C'}=\pi_{C} \cdot g$
.
Proof of Proposition 3·1. One has
 \begin{align*}s_n(C)&= \sum_{C' \in [C]} \frac{(q+1-\#C'(\mathbb{F}_q))^n}{\# \textrm{Aut}_{\mathbb{F}_q}(C')} = \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \frac{(q+1-\#C'(\mathbb{F}_q))^n}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)}\\[5pt] &= \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \frac{\textrm{Tr}(\pi_{C'})^n}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} = \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \frac{\textrm{Tr}((\pi_{C'})^{\otimes n})}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)}\\[5pt] &= \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \frac{\textrm{Tr}((\pi_C \cdot g)^{\otimes n})}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} = \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \frac{\textrm{Tr}(\pi_C^{\otimes n}\cdot g^{\otimes n})}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \\[5pt] &= \textrm{Tr}\Biggl(\pi_C^{\otimes n} \cdot \frac{1}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} g^{\otimes n}\Biggr) = \textrm{Tr}(\pi_C^{\otimes n} \cdot P_{G_n})\,.\end{align*}
\begin{align*}s_n(C)&= \sum_{C' \in [C]} \frac{(q+1-\#C'(\mathbb{F}_q))^n}{\# \textrm{Aut}_{\mathbb{F}_q}(C')} = \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \frac{(q+1-\#C'(\mathbb{F}_q))^n}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)}\\[5pt] &= \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \frac{\textrm{Tr}(\pi_{C'})^n}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} = \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \frac{\textrm{Tr}((\pi_{C'})^{\otimes n})}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)}\\[5pt] &= \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \frac{\textrm{Tr}((\pi_C \cdot g)^{\otimes n})}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} = \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \frac{\textrm{Tr}(\pi_C^{\otimes n}\cdot g^{\otimes n})}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \\[5pt] &= \textrm{Tr}\Biggl(\pi_C^{\otimes n} \cdot \frac{1}{\# \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} \sum_{g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)} g^{\otimes n}\Biggr) = \textrm{Tr}(\pi_C^{\otimes n} \cdot P_{G_n})\,.\end{align*}
The first equality is by definition, the second one by Lemma 3·2, the third one by the Weil Conjectures, the fourth one is a classical property of the tensor product of matrices (see for instance [ Reference SerreSer98 , chapter 2 proposition 2]), the fifth one is [ Reference Meagher and TopMT10 , proposition 11], the sixth one is Lemma 3·3(i), the seventh is the commutativity of the sum and the trace of matrices, and the eighth is Lemma 3·3(ii).
Now, since for every
![]() $g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
we have
$g \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
we have
![]() $g \circ {Fr} = {Fr} \circ g'$
for some
$g \circ {Fr} = {Fr} \circ g'$
for some
![]() $g' \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
, we see that
$g' \in \textrm{Aut}_{\overline{\mathbb{F}}_q}(C)$
, we see that
![]() $\pi_C^{\otimes n}$
commutes with
$\pi_C^{\otimes n}$
commutes with
![]() $P_{G_{n}}$
, hence the eigenvalues of their product are the product of the eigenvalues. It is well known that the complex eigenvalues of
$P_{G_{n}}$
, hence the eigenvalues of their product are the product of the eigenvalues. It is well known that the complex eigenvalues of
![]() $\pi_C$
, and therefore of
$\pi_C$
, and therefore of
![]() $\pi_C^{\otimes n}$
, are algebraic integers, while the eigenvalues of
$\pi_C^{\otimes n}$
, are algebraic integers, while the eigenvalues of
![]() $P_{G_n}$
are 0 or 1. We conclude that the trace is an algebraic integer as well. Now the conclusion follows since we know that
$P_{G_n}$
are 0 or 1. We conclude that the trace is an algebraic integer as well. Now the conclusion follows since we know that
![]() $s_n(C)$
is also a rational number, so it must be an integer.
$s_n(C)$
is also a rational number, so it must be an integer.
For
![]() $\mathcal{X}=\mathcal{M}_g$
or
$\mathcal{X}=\mathcal{M}_g$
or
![]() $\mathcal{H}_g$
we denote by
$\mathcal{H}_g$
we denote by
![]() $S_{n}(q,\mathcal{X})$
the sum of the
$S_{n}(q,\mathcal{X})$
the sum of the
![]() $s_n(C)$
when C runs over a set of representatives for the
$s_n(C)$
when C runs over a set of representatives for the
![]() $\overline{\mathbb{F}}_q$
-isomorphism classes of curves in
$\overline{\mathbb{F}}_q$
-isomorphism classes of curves in
![]() $\mathcal{X}$
over
$\mathcal{X}$
over
![]() $\mathbb{F}_q$
. Then, for two polynomials f and g, let
$\mathbb{F}_q$
. Then, for two polynomials f and g, let
![]() $[f/g]$
denote the polynomial quotient in the Euclidian division of f by g. In Theorem 3·4 and Remark 3·5, the polynomial quotients correspond to the stable part of the cohomology, see [
Reference Miller, Patzt and PetersenMPP19
, section 1·5] together with [
Reference BergströmBer09
, section 13].
$[f/g]$
denote the polynomial quotient in the Euclidian division of f by g. In Theorem 3·4 and Remark 3·5, the polynomial quotients correspond to the stable part of the cohomology, see [
Reference Miller, Patzt and PetersenMPP19
, section 1·5] together with [
Reference BergströmBer09
, section 13].
Theorem 3·4.
For every
![]() $g \geq 2$
and prime power q we have
$g \geq 2$
and prime power q we have
 \begin{align*}S_2(q,\mathcal{H}_g) &= \, [q^{2g}]-1 \\[5pt] [2ex]S_4(q,\mathcal{H}_g) &= \left [\frac{q^{2g} (3q^2+q+1)}{q+1} \right]\\[5pt] &\qquad -\frac{1}{2}(q-1)(q-2)(q+1)g^2+\frac{1}{2}(-q^3+2q^2-7q+2)g-3q+2 \\[5pt] [2ex]S_6(q,\mathcal{H}_g) &= \left [\frac{q^{2g}(15q^4+16q^2+2q+1)}{(q+1)^2}\right]\\[5pt] &\qquad -\frac{1}{24}(q-1)(q-3)(q+1)(q^3-6q^2+4q+13)g^4 \\[5pt] &\qquad -\frac{1}{12}(q+1)(q-3)^2(q^3-4q^2+18q-3)g^3\\[5pt] &\qquad+\frac{1}{24}(q^6-9q^5-99q^4+382q^3-469q^2+491q-9)g^2 \\[5pt] &\qquad+\frac{1}{12}(q^6-9q^5-19q^4+78q^3-423q^2+567q-723)g-15q^2\\[5pt] &\qquad +30q-61-\delta_{q} \, \frac{5}{8}g(g-1)(g-2)\bigl((g-3)(q-1)-4\bigr)\,,\end{align*}
\begin{align*}S_2(q,\mathcal{H}_g) &= \, [q^{2g}]-1 \\[5pt] [2ex]S_4(q,\mathcal{H}_g) &= \left [\frac{q^{2g} (3q^2+q+1)}{q+1} \right]\\[5pt] &\qquad -\frac{1}{2}(q-1)(q-2)(q+1)g^2+\frac{1}{2}(-q^3+2q^2-7q+2)g-3q+2 \\[5pt] [2ex]S_6(q,\mathcal{H}_g) &= \left [\frac{q^{2g}(15q^4+16q^2+2q+1)}{(q+1)^2}\right]\\[5pt] &\qquad -\frac{1}{24}(q-1)(q-3)(q+1)(q^3-6q^2+4q+13)g^4 \\[5pt] &\qquad -\frac{1}{12}(q+1)(q-3)^2(q^3-4q^2+18q-3)g^3\\[5pt] &\qquad+\frac{1}{24}(q^6-9q^5-99q^4+382q^3-469q^2+491q-9)g^2 \\[5pt] &\qquad+\frac{1}{12}(q^6-9q^5-19q^4+78q^3-423q^2+567q-723)g-15q^2\\[5pt] &\qquad +30q-61-\delta_{q} \, \frac{5}{8}g(g-1)(g-2)\bigl((g-3)(q-1)-4\bigr)\,,\end{align*}
where
![]() $\delta_q$
is equal to 1 if
$\delta_q$
is equal to 1 if
![]() $q \equiv 0 \bmod 2$
and 0 otherwise.
$q \equiv 0 \bmod 2$
and 0 otherwise.
Proof. In [
Reference BergströmBer09
, section 7,10] it is described how to compute
![]() $S_i(q,\mathcal{H}_g)$
for
$S_i(q,\mathcal{H}_g)$
for
![]() $i=2,4$
and 6. Note that in the notation of [
Reference BergströmBer09
],
$i=2,4$
and 6. Note that in the notation of [
Reference BergströmBer09
],
![]() $S_i(q)$
equals
$S_i(q)$
equals
![]() $a_{1^i}|_g$
.
$a_{1^i}|_g$
.
Remark 3·5. From [
Reference BergströmBer09
, section 7,10] we see that the information missing to compute
![]() $S_8(q,\mathcal{H}_g)$
for any
$S_8(q,\mathcal{H}_g)$
for any
![]() $g \geq 3$
, is
$g \geq 3$
, is
![]() $S_8(q,\mathcal{M}_{1,1})$
,
$S_8(q,\mathcal{M}_{1,1})$
,
![]() $S_8(q,\mathcal{H}_2)$
and
$S_8(q,\mathcal{H}_2)$
and
 \begin{equation} \sum_{(C,p) \in \mathcal{M}'_{\!\!1,1}(\mathbb{F}_q)} \frac{(q+1-\#C'(\mathbb{F}_q))^6 (q+1-r_1(C))^2}{\# \textrm{Aut}_{\mathbb{F}_q}(C)}\,,\end{equation}
\begin{equation} \sum_{(C,p) \in \mathcal{M}'_{\!\!1,1}(\mathbb{F}_q)} \frac{(q+1-\#C'(\mathbb{F}_q))^6 (q+1-r_1(C))^2}{\# \textrm{Aut}_{\mathbb{F}_q}(C)}\,,\end{equation}
in the notation of [
Reference BergströmBer09
, section 12]. Here,
![]() $q+1-r_1(C)$
is the number of ramification points over
$q+1-r_1(C)$
is the number of ramification points over
![]() $\mathbb{F}_q$
of (C,p) as a double cover of
$\mathbb{F}_q$
of (C,p) as a double cover of
![]() $\mathbb{P}^1$
. For every q,
$\mathbb{P}^1$
. For every q,
![]() $S_8(q,\mathcal{H}_2)$
can be determined through the information in [
Reference PetersenPet15
, theorem 2·1]. A level two structure on an elliptic curve can be described in terms of a marking of its ramification points. For odd q, the cohomology of local systems on
$S_8(q,\mathcal{H}_2)$
can be determined through the information in [
Reference PetersenPet15
, theorem 2·1]. A level two structure on an elliptic curve can be described in terms of a marking of its ramification points. For odd q, the cohomology of local systems on
![]() $\mathcal{M}_{1,1}[2] \otimes \overline{\mathbb{F}}_q$
(the moduli space of elliptic curves with a level two structure) and its structure as a representation of
$\mathcal{M}_{1,1}[2] \otimes \overline{\mathbb{F}}_q$
(the moduli space of elliptic curves with a level two structure) and its structure as a representation of
![]() $\textrm{SL}(2,\mathbb{F}_2) \cong \mathbb{S}_3$
, is well known via the Eichler–Shimura isomorphism, see [
Reference DeligneDel71
] and [
Reference FaltingsFal87
, theorem 6]. Using this we can also compute (3·2). Putting these results together we find that for every
$\textrm{SL}(2,\mathbb{F}_2) \cong \mathbb{S}_3$
, is well known via the Eichler–Shimura isomorphism, see [
Reference DeligneDel71
] and [
Reference FaltingsFal87
, theorem 6]. Using this we can also compute (3·2). Putting these results together we find that for every
![]() $g \geq 2$
and odd q, we have
$g \geq 2$
and odd q, we have
 \begin{multline*}S_8(q,\mathcal{H}_g)=\left[\frac{q^{2g}(105q^6-105q^5+273q^4-83q^3+66q^2+3q+1)}{(q+1)^3}\right] \\[5pt] \shoveleft{\hskip6em -\frac{1}{720}(q-1)(q-3)(q-4)(q-5)(q+1)^2(q^3-9q^2+15q+33) g^6} \\[5pt] \shoveleft{\hskip6em -\frac{1}{240}(q-3)(q-5)(q+1)(q^6-13q^5+92q^4-280q^3} \\[5pt] \shoveright{+215q^2+565q-100)g^5}\\[5pt] \shoveleft{\hskip6em +\frac{1}{144}(q-3)(q+1)(q^7-18q^6-11q^5+828q^4-3455q^3} \\[5pt] \shoveright{+5826q^2-4947q+48)g^4}\\[5pt] \shoveleft{\hskip6em +\frac{1}{48}(q-3)(q^8-17q^7+55q^6+61q^5-1329q^4+3573q^3} \\[5pt] \shoveright{-3219q^2+2095q+124)g^3}\\[5pt] \shoveleft{\hskip6em +\frac{1}{360} (\!-2q^9+40q^8+19q^7-2480q^6-3470q^5+52390q^4} \\[5pt] \shoveright{-166449q^3+338580q^2-424098 q+453870)g^2} \\[5pt] \shoveleft{\hskip6em +\frac{1}{60} (\!-q^9+20q^8-85q^7-120q^6-214q^5+2530q^4}\\[5pt] \shoveright{-22515q^3+62220q^2-127725q+201870)g}\\[5pt] \shoveleft{\hskip6em -105q^3+420q^2-1218q+2582\,.}\\[5pt] \end{multline*}
\begin{multline*}S_8(q,\mathcal{H}_g)=\left[\frac{q^{2g}(105q^6-105q^5+273q^4-83q^3+66q^2+3q+1)}{(q+1)^3}\right] \\[5pt] \shoveleft{\hskip6em -\frac{1}{720}(q-1)(q-3)(q-4)(q-5)(q+1)^2(q^3-9q^2+15q+33) g^6} \\[5pt] \shoveleft{\hskip6em -\frac{1}{240}(q-3)(q-5)(q+1)(q^6-13q^5+92q^4-280q^3} \\[5pt] \shoveright{+215q^2+565q-100)g^5}\\[5pt] \shoveleft{\hskip6em +\frac{1}{144}(q-3)(q+1)(q^7-18q^6-11q^5+828q^4-3455q^3} \\[5pt] \shoveright{+5826q^2-4947q+48)g^4}\\[5pt] \shoveleft{\hskip6em +\frac{1}{48}(q-3)(q^8-17q^7+55q^6+61q^5-1329q^4+3573q^3} \\[5pt] \shoveright{-3219q^2+2095q+124)g^3}\\[5pt] \shoveleft{\hskip6em +\frac{1}{360} (\!-2q^9+40q^8+19q^7-2480q^6-3470q^5+52390q^4} \\[5pt] \shoveright{-166449q^3+338580q^2-424098 q+453870)g^2} \\[5pt] \shoveleft{\hskip6em +\frac{1}{60} (\!-q^9+20q^8-85q^7-120q^6-214q^5+2530q^4}\\[5pt] \shoveright{-22515q^3+62220q^2-127725q+201870)g}\\[5pt] \shoveleft{\hskip6em -105q^3+420q^2-1218q+2582\,.}\\[5pt] \end{multline*}
Theorem 3·6.
For every
![]() $g\geq 2$
, prime power q and even
$g\geq 2$
, prime power q and even
![]() $n \geq 2$
, let
$n \geq 2$
, let
There exists a hyperelliptic genus-g curve
![]() $C/\mathbb{F}_q$
with
$C/\mathbb{F}_q$
with
![]() $\#C(\mathbb{F}_q)\geq 1+q+ a_q \sqrt{q}$
and a hyperelliptic curve
$\#C(\mathbb{F}_q)\geq 1+q+ a_q \sqrt{q}$
and a hyperelliptic curve
![]() $C'/\mathbb{F}_q$
with
$C'/\mathbb{F}_q$
with
![]() $\#C'(\mathbb{F}_q)\leq 1+q-a_q \sqrt{q}$
.
$\#C'(\mathbb{F}_q)\leq 1+q-a_q \sqrt{q}$
.
Proof. By the above, we see that there are curves
![]() $C_1,\ldots,C_{q^{2g-1}}$
over
$C_1,\ldots,C_{q^{2g-1}}$
over
![]() $\mathbb{F}_q$
such that
$\mathbb{F}_q$
such that
![]() $S_n(q)=\sum_{i=1}^{q^{2g-1}} s_n(C_i)$
. Since n is even, all the
$S_n(q)=\sum_{i=1}^{q^{2g-1}} s_n(C_i)$
. Since n is even, all the
![]() $s_n(C_i)$
are non-negative and so there must be a j such that
$s_n(C_i)$
are non-negative and so there must be a j such that
![]() $s_{n}(C_j) \geq S_n(q)/q^{2g-1}$
. Since
$s_{n}(C_j) \geq S_n(q)/q^{2g-1}$
. Since
 \[s_0(C_j)=\sum_{C\in [C_j]} \frac{1}{\# \textrm{Aut}_{\mathbb{F}_q}(C)}=1,\]
\[s_0(C_j)=\sum_{C\in [C_j]} \frac{1}{\# \textrm{Aut}_{\mathbb{F}_q}(C)}=1,\]
![]() $s_n(C_j)$
can be seen as a weighted average, and it then follows that there is a
$s_n(C_j)$
can be seen as a weighted average, and it then follows that there is a
![]() $C \in [C_j]$
such that
$C \in [C_j]$
such that
![]() $(\#C(\mathbb{F}_q)-q-1)^n \geq S_n(q)/q^{2g-1}$
. This shows that
$(\#C(\mathbb{F}_q)-q-1)^n \geq S_n(q)/q^{2g-1}$
. This shows that
![]() $\#C(\mathbb{F}_q) \leq q+1-a_q\sqrt{q}$
with
$\#C(\mathbb{F}_q) \leq q+1-a_q\sqrt{q}$
with
![]() $a_q=(S_n(q)/q^{2g-1+n/2})^{1/n} $
. The quadratic twist of C gives the curve with the opposite bound.
$a_q=(S_n(q)/q^{2g-1+n/2})^{1/n} $
. The quadratic twist of C gives the curve with the opposite bound.
Using the formulas of Theorem 3·4 and Remark 3·5 we get, for
![]() $i=2$
, 4, 6, and 8, concrete lower bounds for
$i=2$
, 4, 6, and 8, concrete lower bounds for
![]() $(S_n(q,\mathcal{H}_g)/q^{2g-1+n/2})^{1/n}$
valid for q large enough.
$(S_n(q,\mathcal{H}_g)/q^{2g-1+n/2})^{1/n}$
valid for q large enough.
Corollary 3·7.
There exists a hyperelliptic curve of genus g over
![]() $\mathbb{F}_q$
with
$\mathbb{F}_q$
with
![]() $\#C(\mathbb{F}_q) \geq 1+q+a \sqrt{q}$
with:
$\#C(\mathbb{F}_q) \geq 1+q+a \sqrt{q}$
with:
-
(i)
 $a=(S_4(q)/q^{2g+1})^{1/4} \geq 1.3$
for
$a=(S_4(q)/q^{2g+1})^{1/4} \geq 1.3$
for
 $g \geq 3$
and
$g \geq 3$
and
 $q \geq 13$
;
$q \geq 13$
; -
(ii)
 $a=(S_6(q)/q^{2g+2})^{1/6} \geq 1.55$
for
$a=(S_6(q)/q^{2g+2})^{1/6} \geq 1.55$
for
 $g \geq 3$
and
$g \geq 3$
and
 $q \geq 25$
;
$q \geq 25$
; -
(iii)
 $a=(S_8(q)/q^{2g+3})^{1/8} \geq 1.71$
for
$a=(S_8(q)/q^{2g+3})^{1/8} \geq 1.71$
for
 $g \geq 3$
and odd
$g \geq 3$
and odd
 $q \geq 11$
.
$q \geq 11$
.
One sees that the coefficient of the leading term of
![]() $S_n(q)$
controls the growth of the bound on the number of points. This coefficient can be obtained quickly, even when a complete formula for
$S_n(q)$
controls the growth of the bound on the number of points. This coefficient can be obtained quickly, even when a complete formula for
![]() $S_n(q)$
is out of reach, thanks to a relation with representation theory of the compact symplectic group
$S_n(q)$
is out of reach, thanks to a relation with representation theory of the compact symplectic group
![]() $\textrm{USp}_{2g}$
.
$\textrm{USp}_{2g}$
.
Theorem 3·8.
For every
![]() $g \geq 2$
and even
$g \geq 2$
and even
![]() $n \geq 2$
let
$n \geq 2$
let
with
![]() $\mathcal{X}=\mathcal{M}_g$
or
$\mathcal{X}=\mathcal{M}_g$
or
![]() $\mathcal{H}_g$
. Then
$\mathcal{H}_g$
. Then
![]() $\mathfrak{a}_n(g)$
is equal to the number of times the trivial representation appears in the
$\mathfrak{a}_n(g)$
is equal to the number of times the trivial representation appears in the
![]() $\textrm{USp}_{2g}$
-representation
$\textrm{USp}_{2g}$
-representation
![]() $V^{\otimes n}$
with V the standard representation.
$V^{\otimes n}$
with V the standard representation.
Proof. Using Theorem 2·1 with
![]() $f=\textrm{Tr}^n$
, we see that
$f=\textrm{Tr}^n$
, we see that
 \begin{equation} \mathfrak{a}_n(g)= \int_{{(\theta_1,\ldots,\theta_g)}\in [0,\pi]^g } \biggl(\sum_{j=1}^g 2 \cos(\theta_j) \biggr)^n d\mu_g(\theta_1,\ldots,\theta_g)\,,\end{equation}
\begin{equation} \mathfrak{a}_n(g)= \int_{{(\theta_1,\ldots,\theta_g)}\in [0,\pi]^g } \biggl(\sum_{j=1}^g 2 \cos(\theta_j) \biggr)^n d\mu_g(\theta_1,\ldots,\theta_g)\,,\end{equation}
and that this integral also can be written as
By the orthogonality of characters it follows that this integral counts the number of times that the trivial representation appears in the nth tensor product of the standard representation.
The sequence
![]() $\mathfrak{a}_n(g)$
is called a moment sequence in [
Reference Kedlaya and SutherlandKS09
]; in their notation it equals
$\mathfrak{a}_n(g)$
is called a moment sequence in [
Reference Kedlaya and SutherlandKS09
]; in their notation it equals
![]() $M[s_1](n)$
. In this paper Kedlaya and Sutherland give an effective formula to compute
$M[s_1](n)$
. In this paper Kedlaya and Sutherland give an effective formula to compute
![]() $\mathfrak{a}_n(g)$
in terms of a sum of determinants of binomial expressions. However, to prove the following limit result, it is easier to use the integral.
$\mathfrak{a}_n(g)$
in terms of a sum of determinants of binomial expressions. However, to prove the following limit result, it is easier to use the integral.
Theorem 3·9.
For every
![]() $g \geq 2$
, we have
$g \geq 2$
, we have
Proof. First notice that since
![]() $\lvert\cos(\theta)\rvert \leq 1$
we have
$\lvert\cos(\theta)\rvert \leq 1$
we have
![]() $\lvert a_n\rvert \leq (2g)^n$
, so
$\lvert a_n\rvert \leq (2g)^n$
, so
Let us now change variables by setting
![]() $t_i=2\cos(\theta_i)$
. Then Equation (3·3) becomes
$t_i=2\cos(\theta_i)$
. Then Equation (3·3) becomes
 \begin{equation} \mathfrak{a}_n(g)= \int_{{(t_1,\ldots,t_g)}\in [\!-\!2,2]^g } \biggl(\sum_{j=1}^g t_j \biggr)^n\prod_{j=1}^g\sqrt{4-t_j^2}\prod_{1\leq j\leq k\leq g}(t_j-t_k)^2 \,dt_1\ldots dt_g.\end{equation}
\begin{equation} \mathfrak{a}_n(g)= \int_{{(t_1,\ldots,t_g)}\in [\!-\!2,2]^g } \biggl(\sum_{j=1}^g t_j \biggr)^n\prod_{j=1}^g\sqrt{4-t_j^2}\prod_{1\leq j\leq k\leq g}(t_j-t_k)^2 \,dt_1\ldots dt_g.\end{equation}
Since all factors inside the integral of
![]() $\mathfrak{a}_{2n}(g)$
are positive, the value of the integral is greater than the one taken on any sub-domain of
$\mathfrak{a}_{2n}(g)$
are positive, the value of the integral is greater than the one taken on any sub-domain of
![]() $[\!-\!2,2]^g$
. Fix
$[\!-\!2,2]^g$
. Fix
![]() $0<\varepsilon<1$
and define
$0<\varepsilon<1$
and define
for
![]() $j=1,\ldots,g$
. The sub-domain
$j=1,\ldots,g$
. The sub-domain
![]() $S=I_1 \times \cdots \times I_g$
is constructed so that the values of the
$S=I_1 \times \cdots \times I_g$
is constructed so that the values of the
![]() $t_i$
are separated by at least
$t_i$
are separated by at least
![]() ${\varepsilon}/({2g-1})$
and are close to 2. Then
${\varepsilon}/({2g-1})$
and are close to 2. Then
 \begin{align*}\mathfrak{a}_{2n}(g)&\geq \int_{(t_1,\ldots,t_g) \in S}\biggl(\sum_{j=1}^g t_j \biggr)^{2n}\prod_{j=1}^g\sqrt{4-t_j^2}\prod_{1\leq j\leq k\leq g}(t_j-t_k)^2 \,dt_1\cdots dt_g \\[5pt] &\geq \int_{(t_1,\ldots,t_g) \in S} (2g-2\varepsilon g)^{2n} \cdot \varepsilon^g \cdot \left(\frac{\varepsilon}{2g-1}\right)^{g(g-1)} \,dt_1\cdots dt_g \\[5pt] &\geq \left(\frac{\varepsilon}{2g-1}\right)^{g} \cdot (2g-2\varepsilon g)^{2n} \cdot \varepsilon^g \cdot \left(\frac{\varepsilon}{2g-1}\right)^{g(g-1)}.\end{align*}
\begin{align*}\mathfrak{a}_{2n}(g)&\geq \int_{(t_1,\ldots,t_g) \in S}\biggl(\sum_{j=1}^g t_j \biggr)^{2n}\prod_{j=1}^g\sqrt{4-t_j^2}\prod_{1\leq j\leq k\leq g}(t_j-t_k)^2 \,dt_1\cdots dt_g \\[5pt] &\geq \int_{(t_1,\ldots,t_g) \in S} (2g-2\varepsilon g)^{2n} \cdot \varepsilon^g \cdot \left(\frac{\varepsilon}{2g-1}\right)^{g(g-1)} \,dt_1\cdots dt_g \\[5pt] &\geq \left(\frac{\varepsilon}{2g-1}\right)^{g} \cdot (2g-2\varepsilon g)^{2n} \cdot \varepsilon^g \cdot \left(\frac{\varepsilon}{2g-1}\right)^{g(g-1)}.\end{align*}
So
![]() $\liminf_{n \to \infty} (\mathfrak{a}_{2n}(g))^{1/2n}\geq2g$
and the result follows.
$\liminf_{n \to \infty} (\mathfrak{a}_{2n}(g))^{1/2n}\geq2g$
and the result follows.
4. Lower bounds from explicit constructions
Corollary 2·3 shows that for a fixed genus g and fixed
![]() $\varepsilon>0$
, for every large enough q there is a hyperelliptic curve
$\varepsilon>0$
, for every large enough q there is a hyperelliptic curve
![]() $C/\mathbb{F}_q$
of genus g whose number of points is within
$C/\mathbb{F}_q$
of genus g whose number of points is within
![]() $\varepsilon\sqrt{q}$
of the Weil bound. In this section we prove a result that is much weaker than this, but that has the advantages of working for every q and
$\varepsilon\sqrt{q}$
of the Weil bound. In this section we prove a result that is much weaker than this, but that has the advantages of working for every q and
![]() $g\ge 2$
and of being constructive — see Section 4·3.
$g\ge 2$
and of being constructive — see Section 4·3.
Theorem 4·1.
Let
![]() $g>1$
be an integer and let q be a prime power.
$g>1$
be an integer and let q be a prime power.
-
(i) If q is odd, there is a hyperelliptic curve
 $C/\mathbb{F}_q$
of genus g with
$C/\mathbb{F}_q$
of genus g with  \[ \#C(\mathbb{F}_q) > \begin{cases} 1 + q + 4\sqrt{q} - 5 & \text{if $q<512$};\\[5pt] 1 + q + 4\sqrt{q} - 32 & \text{if $q>512$}.\\[5pt] \end{cases} \]
\[ \#C(\mathbb{F}_q) > \begin{cases} 1 + q + 4\sqrt{q} - 5 & \text{if $q<512$};\\[5pt] 1 + q + 4\sqrt{q} - 32 & \text{if $q>512$}.\\[5pt] \end{cases} \]
-
(ii) If q is even, there is a hyperelliptic curve
 $C/\mathbb{F}_q$
of genus g with
$C/\mathbb{F}_q$
of genus g with  \[ \#C(\mathbb{F}_q) > \begin{cases} 1 + q + 4\sqrt{q} - 5 & \text{if $q\le 8$};\\[5pt] 1 + q + 4\sqrt{q} - 12 & \text{if $q>8$}.\\[5pt] \end{cases} \]
\[ \#C(\mathbb{F}_q) > \begin{cases} 1 + q + 4\sqrt{q} - 5 & \text{if $q\le 8$};\\[5pt] 1 + q + 4\sqrt{q} - 12 & \text{if $q>8$}.\\[5pt] \end{cases} \]
Remark 4·2. When q is small with respect to g, there are in fact hyperelliptic curves of genus g over
![]() $\mathbb{F}_q$
having
$\mathbb{F}_q$
having
![]() $2q+2$
rational points, the largest number possible for a hyperelliptic curve over
$2q+2$
rational points, the largest number possible for a hyperelliptic curve over
![]() $\mathbb{F}_q$
of any genus. The sharpest result in this direction that we are aware of is [
Reference PogildiakovPog17
, theorem 1·6], which implies that for
$\mathbb{F}_q$
of any genus. The sharpest result in this direction that we are aware of is [
Reference PogildiakovPog17
, theorem 1·6], which implies that for
![]() $g\ge 2$
, if q is odd and
$g\ge 2$
, if q is odd and
![]() $q\le 2g+3$
, or if q is even and
$q\le 2g+3$
, or if q is even and
![]() $q\le g+1$
, then there is a hyperelliptic curve of genus g over
$q\le g+1$
, then there is a hyperelliptic curve of genus g over
![]() $\mathbb{F}_q$
with
$\mathbb{F}_q$
with
![]() $2q+2$
rational points. (The cited result speaks of curves with no points, but the quadratic twist of such a curve has
$2q+2$
rational points. (The cited result speaks of curves with no points, but the quadratic twist of such a curve has
![]() $2q+2$
points.)
$2q+2$
points.)
The basic idea of our proof of Theorem 4·1 is to create a tower of double covers of hyperelliptic curves, each with at least as many rational points as the one below it. Here is the structure of the argument in the case where q is odd: Let C be a hyperelliptic curve of genus g over
![]() $\mathbb{F}_q$
. If C has exactly two rational Weierstrass points then we can construct hyperelliptic double covers D of C, one of genus 2g and one of genus
$\mathbb{F}_q$
. If C has exactly two rational Weierstrass points then we can construct hyperelliptic double covers D of C, one of genus 2g and one of genus
![]() $2g+1$
, such that D has exactly two rational Weierstrass points and such that
$2g+1$
, such that D has exactly two rational Weierstrass points and such that
![]() $\#D(\mathbb{F}_q)\ge \#C(\mathbb{F}_q)$
. By using a double-and-add process starting from a curve of genus 2, we can reach every genus whose binary expansion starts with 10; starting from a curve of genus 3, we can reach every genus whose binary expansion starts with 11. Thus, the lower bound we get in the statement of the theorem is essentially the largest number of points we can obtain on a curve of genus 2 that is suitable as a starting curve for our construction.
$\#D(\mathbb{F}_q)\ge \#C(\mathbb{F}_q)$
. By using a double-and-add process starting from a curve of genus 2, we can reach every genus whose binary expansion starts with 10; starting from a curve of genus 3, we can reach every genus whose binary expansion starts with 11. Thus, the lower bound we get in the statement of the theorem is essentially the largest number of points we can obtain on a curve of genus 2 that is suitable as a starting curve for our construction.
In Section 4·1 we flesh out the tower-building argument for odd q sketched in the preceding paragraph. We also explain how to construct appropriate base curves of genus 2 by gluing together elliptic curves with many points, and appropriate base curves of genus 3 by taking unramified double covers of such genus-2 curves. In Section 4·2 we show how to modify the argument for odd q in order to deal with the fact that in characteristic 2, hyperelliptic curves are Artin–Schreier extensions of
![]() $\mathbb{P}^1$
rather than Kummer extensions.
$\mathbb{P}^1$
rather than Kummer extensions.
The double-cover argument that we use to prove Theorem 4·1 was inspired by a similar double-cover argument from [
Reference Elkies, Howe, Kresch, Poonen, Wetherell and ZieveEHK+04
], which shows that if C is a not-necessarily-hyperelliptic curve of genus g over
![]() $\mathbb{F}_q$
, then for every
$\mathbb{F}_q$
, then for every
![]() $h\ge 4g$
there is a curve
$h\ge 4g$
there is a curve
![]() $D/\mathbb{F}_q$
of genus h that is a double cover of C and that has at least as many rational points as does C.
$D/\mathbb{F}_q$
of genus h that is a double cover of C and that has at least as many rational points as does C.
4·1. Odd characteristic
In this section, we prove Theorem 4·1 for finite fields of odd characteristic. We start by stating and proving several lemmas that we will use in the proof.
Lemma 4·3.
Let q be an odd prime power and let
![]() $C/\mathbb{F}_q$
be a hyperelliptic curve of genus g with fewer than q rational Weierstrass points. Then there is a hyperelliptic curve D of genus
$C/\mathbb{F}_q$
be a hyperelliptic curve of genus g with fewer than q rational Weierstrass points. Then there is a hyperelliptic curve D of genus
![]() $2g+1$
that is a double cover of C and that has at least as many rational points as does C.
$2g+1$
that is a double cover of C and that has at least as many rational points as does C.
If C has exactly two rational Weierstrass points, then D can be chosen to have exactly two rational Weierstrass points.
Remark 4·4. If
![]() $C/\mathbb{F}_q$
is a hyperelliptic curve with
$C/\mathbb{F}_q$
is a hyperelliptic curve with
![]() $\#C(\mathbb{F}_q) > q + 3$
then C has fewer than q rational Weierstrass points.
$\#C(\mathbb{F}_q) > q + 3$
then C has fewer than q rational Weierstrass points.
Proof. Let
![]() $\varphi$
be the canonical map from C to
$\varphi$
be the canonical map from C to
![]() $\mathbb{P}^1$
. There are at least 2 points of
$\mathbb{P}^1$
. There are at least 2 points of
![]() $\mathbb{P}^1$
that do not ramify in
$\mathbb{P}^1$
that do not ramify in
![]() $\varphi$
, and we can pick two such points and choose a coordinate function x on
$\varphi$
, and we can pick two such points and choose a coordinate function x on
![]() $\mathbb{P}^1$
so that those two points lie at 0 and
$\mathbb{P}^1$
so that those two points lie at 0 and
![]() $\infty$
. That means that C has a hyperelliptic model of the form
$\infty$
. That means that C has a hyperelliptic model of the form
![]() $y^2 = f$
, where
$y^2 = f$
, where
![]() $f\in \mathbb{F}_q[x]$
is a separable polynomial of degree
$f\in \mathbb{F}_q[x]$
is a separable polynomial of degree
![]() $2g+2$
such that
$2g+2$
such that
![]() $f(0)\ne 0$
.
$f(0)\ne 0$
.
Let n be a nonsquare in
![]() $\mathbb{F}_q$
, and consider the two hyperelliptic curves
$\mathbb{F}_q$
, and consider the two hyperelliptic curves
![]() $D\colon y^2 = f(x^2)$
and
$D\colon y^2 = f(x^2)$
and
![]() $D'\colon y^2 = f(nx^2)$
. We note that both
$D'\colon y^2 = f(nx^2)$
. We note that both
![]() $f(x^2)$
and
$f(x^2)$
and
![]() $f(nx^2)$
are separable polynomials of degree
$f(nx^2)$
are separable polynomials of degree
![]() $4g+4$
, so both D and D
′ have genus
$4g+4$
, so both D and D
′ have genus
![]() $2g+1$
. The two natural double covers
$2g+1$
. The two natural double covers
![]() $D\to C$
and
$D\to C$
and
![]() $D'\to C$
are quadratic twists of one another, and it follows that
$D'\to C$
are quadratic twists of one another, and it follows that
![]() $\#D(\mathbb{F}_q) + \#D'(\mathbb{F}_q) = 2\#C(\mathbb{F}_q)$
. Therefore, one of these two curves has at least as many rational points as does C.
$\#D(\mathbb{F}_q) + \#D'(\mathbb{F}_q) = 2\#C(\mathbb{F}_q)$
. Therefore, one of these two curves has at least as many rational points as does C.
Suppose C has exactly two rational Weierstrass points. This time, we choose our coordinate function x on
![]() $\mathbb{P}^1$
so that these two points lie over
$\mathbb{P}^1$
so that these two points lie over
![]() $x = 1$
and
$x = 1$
and
![]() $x = n$
, where n is a nonsquare element of
$x = n$
, where n is a nonsquare element of
![]() $\mathbb{F}_q$
. Then
$\mathbb{F}_q$
. Then
![]() $x=0$
and
$x=0$
and
![]() $x=\infty$
do not ramify in
$x=\infty$
do not ramify in
![]() $\varphi$
, so again we have a model of the form
$\varphi$
, so again we have a model of the form
![]() $y^2 = f$
, where
$y^2 = f$
, where
![]() $f\in \mathbb{F}_q[x]$
is a separable polynomial of degree
$f\in \mathbb{F}_q[x]$
is a separable polynomial of degree
![]() $2g+2$
such that
$2g+2$
such that
![]() $f(0)\ne 0$
, and we proceed as before. Note that the Weierstrass point (1,0) of C splits into two rational Weierstrass points of D and (n,0) splits into nonrational points of D, while (n,0) splits into two rational Weierstrass points of D
′ and (1,0) splits into nonrational points of D
′. Therefore, each of D and D
′ has exactly two rational Weierstrass points, so no matter which one we choose as our cover, we have the desired number of rational Weierstrass points.
$f(0)\ne 0$
, and we proceed as before. Note that the Weierstrass point (1,0) of C splits into two rational Weierstrass points of D and (n,0) splits into nonrational points of D, while (n,0) splits into two rational Weierstrass points of D
′ and (1,0) splits into nonrational points of D
′. Therefore, each of D and D
′ has exactly two rational Weierstrass points, so no matter which one we choose as our cover, we have the desired number of rational Weierstrass points.
Lemma 4·5.
Let q be an odd prime power and let
![]() $C/\mathbb{F}_q$
be a hyperelliptic curve of genus g with exactly two rational Weierstrass points. Then there is a hyperelliptic curve
$C/\mathbb{F}_q$
be a hyperelliptic curve of genus g with exactly two rational Weierstrass points. Then there is a hyperelliptic curve
![]() $D/\mathbb{F}_q$
of genus 2g that is a double cover of C, that has exactly two rational Weierstrass points, and that has at least as many rational points as does C.
$D/\mathbb{F}_q$
of genus 2g that is a double cover of C, that has exactly two rational Weierstrass points, and that has at least as many rational points as does C.
Proof of Lemma 4·5. Let
![]() $\varphi$
be the canonical map from C to
$\varphi$
be the canonical map from C to
![]() $\mathbb{P}^1$
, and choose a coordinate function x on
$\mathbb{P}^1$
, and choose a coordinate function x on
![]() $\mathbb{P}^1$
so that the two rational Weierstrass points of C lie over
$\mathbb{P}^1$
so that the two rational Weierstrass points of C lie over
![]() $x=0$
and
$x=0$
and
![]() $x=\infty$
. Then C has a hyperelliptic model of the form
$x=\infty$
. Then C has a hyperelliptic model of the form
![]() $y^2 = f$
, where
$y^2 = f$
, where
![]() $f\in \mathbb{F}_q[x]$
is a separable polynomial of degree
$f\in \mathbb{F}_q[x]$
is a separable polynomial of degree
![]() $2g+1$
such that
$2g+1$
such that
![]() $f(0) = 0$
and such that f has no other rational roots. By scaling x and y, if necessary, we can also assume that f is monic. For every nonzero
$f(0) = 0$
and such that f has no other rational roots. By scaling x and y, if necessary, we can also assume that f is monic. For every nonzero
![]() $a\in\mathbb{F}_q$
let
$a\in\mathbb{F}_q$
let
![]() $h_a(x) = f(x^2 - a^2)$
, so that
$h_a(x) = f(x^2 - a^2)$
, so that
![]() $h_a$
is a monic separable polynomial in
$h_a$
is a monic separable polynomial in
![]() $\mathbb{F}_q[x]$
of degree
$\mathbb{F}_q[x]$
of degree
![]() $4g+2$
whose only rational roots are
$4g+2$
whose only rational roots are
![]() $x = a$
and
$x = a$
and
![]() $x = -a$
. Let
$x = -a$
. Let
![]() $D_a$
be the hyperelliptic curve
$D_a$
be the hyperelliptic curve
![]() $y^2 = h_a$
. Then
$y^2 = h_a$
. Then
![]() $D_a$
has genus 2g and is a double cover of C, and
$D_a$
has genus 2g and is a double cover of C, and
![]() $D_a$
has exactly two rational Weierstrass points. We will show that there is a value of a so that
$D_a$
has exactly two rational Weierstrass points. We will show that there is a value of a so that
![]() $\#D_a(\mathbb{F}_q)\ge\#C(\mathbb{F}_q).$
$\#D_a(\mathbb{F}_q)\ge\#C(\mathbb{F}_q).$
Let
![]() $\chi$
denote the quadratic character on
$\chi$
denote the quadratic character on
![]() $\mathbb{F}_q$
, so that for
$\mathbb{F}_q$
, so that for
![]() $z\in\mathbb{F}_q$
we have
$z\in\mathbb{F}_q$
we have
![]() $\chi(z) = 1$
if z is a nonzero square,
$\chi(z) = 1$
if z is a nonzero square,
![]() $\chi(z) = 0$
if
$\chi(z) = 0$
if
![]() $z=0$
, and
$z=0$
, and
![]() $\chi(z) = -1$
if z is a nonsquare. Consider the degree-4 map
$\chi(z) = -1$
if z is a nonsquare. Consider the degree-4 map
![]() $D_a\to P^1$
that takes a point (x,y) of
$D_a\to P^1$
that takes a point (x,y) of
![]() $D_a$
to the point
$D_a$
to the point
![]() $x^2 - a^2$
of
$x^2 - a^2$
of
![]() $\mathbb{P}^1$
. A finite point z of
$\mathbb{P}^1$
. A finite point z of
![]() $\mathbb{P}^1$
will have a rational point of D lying over it if and only if there are rational solutions to
$\mathbb{P}^1$
will have a rational point of D lying over it if and only if there are rational solutions to
![]() $x^2 = z + a^2$
and the value of f(z) is a square. Even stronger: The number of rational points of D lying over z is equal to
$x^2 = z + a^2$
and the value of f(z) is a square. Even stronger: The number of rational points of D lying over z is equal to
![]() $(1 + \chi(z+a^2))(1 + \chi(f(z))$
. On the other hand, if
$(1 + \chi(z+a^2))(1 + \chi(f(z))$
. On the other hand, if
![]() $z=\infty$
then there are two rational points of D lying over it, because
$z=\infty$
then there are two rational points of D lying over it, because
![]() $h_a$
is monic of even degree. Thus the number of rational points on D is given by
$h_a$
is monic of even degree. Thus the number of rational points on D is given by
 \begin{align*}\#D_a(\mathbb{F}_q)&= 2 + \sum_{z\in \mathbb{F}_q} (1 + \chi(z+a^2))(1 + \chi(f(z))\\[5pt] &= 2 + \sum_{z\in \mathbb{F}_q} (1 + \chi(f(z))) + \sum_{z\in \mathbb{F}_q} \chi(z+a^2) + \sum_{z\in \mathbb{F}_q} \chi(z+a^2)\chi(f(z))\\[5pt] &= 1 + \#C(\mathbb{F}_q) + \sum_{z\in \mathbb{F}_q} \chi(z+a^2) + \sum_{z\in \mathbb{F}_q} \chi(z+a^2)\chi(f(z))\\[5pt] &= 1 + \#C(\mathbb{F}_q) + \sum_{z\in \mathbb{F}_q} \chi(z+a^2)\chi(f(z))\,,\end{align*}
\begin{align*}\#D_a(\mathbb{F}_q)&= 2 + \sum_{z\in \mathbb{F}_q} (1 + \chi(z+a^2))(1 + \chi(f(z))\\[5pt] &= 2 + \sum_{z\in \mathbb{F}_q} (1 + \chi(f(z))) + \sum_{z\in \mathbb{F}_q} \chi(z+a^2) + \sum_{z\in \mathbb{F}_q} \chi(z+a^2)\chi(f(z))\\[5pt] &= 1 + \#C(\mathbb{F}_q) + \sum_{z\in \mathbb{F}_q} \chi(z+a^2) + \sum_{z\in \mathbb{F}_q} \chi(z+a^2)\chi(f(z))\\[5pt] &= 1 + \#C(\mathbb{F}_q) + \sum_{z\in \mathbb{F}_q} \chi(z+a^2)\chi(f(z))\,,\end{align*}
where the third equality follows from the fact that
![]() $\#C(\mathbb{F}_q) = 1 + \sum_{z\in \mathbb{F}_q} (1 + \chi(f(z)))$
and the final equality follows from the fact that the sum over all z of
$\#C(\mathbb{F}_q) = 1 + \sum_{z\in \mathbb{F}_q} (1 + \chi(f(z)))$
and the final equality follows from the fact that the sum over all z of
![]() $\chi(z+a^2)$
is zero, since the number of nonzero squares in
$\chi(z+a^2)$
is zero, since the number of nonzero squares in
![]() $\mathbb{F}_q$
is equal to the number of nonsquares. Define
$\mathbb{F}_q$
is equal to the number of nonsquares. Define
so that
![]() $\#D_a(\mathbb{F}_q) = 1 + \#C(\mathbb{F}_q) + N_a$
. To complete the proof, we need only show that there is a nonzero a such that
$\#D_a(\mathbb{F}_q) = 1 + \#C(\mathbb{F}_q) + N_a$
. To complete the proof, we need only show that there is a nonzero a such that
![]() $N_a \ge -1$
.
$N_a \ge -1$
.
We will also need an analog of
![]() $N_a$
when
$N_a$
when
![]() $a = 0$
, which we define as follows. Let c be the coefficient of x in the polynomial f, and let
$a = 0$
, which we define as follows. Let c be the coefficient of x in the polynomial f, and let
![]() $h_0$
be the monic separable polynomial of degree 4g such that
$h_0$
be the monic separable polynomial of degree 4g such that
![]() $f(x^2) = x^2 h_0(x)$
. Let
$f(x^2) = x^2 h_0(x)$
. Let
![]() $D_0$
be the hyperelliptic curve of genus
$D_0$
be the hyperelliptic curve of genus
![]() $2g-1$
given by
$2g-1$
given by
![]() $y^2 = h_0$
. Arguing as before, we find that
$y^2 = h_0$
. Arguing as before, we find that
 \begin{align*}\#D_0(\mathbb{F}_q)&= 2 + (1 + \chi(c)) + \sum_{z\in \mathbb{F}_q^\times} (1 + \chi(z))(1 + \chi(f(z))\\[5pt] &= 3 + \chi(c) + \sum_{z\in \mathbb{F}_q^\times} (1 + \chi(f(z))) + \sum_{z\in \mathbb{F}_q^\times} \chi(z) + \sum_{z\in \mathbb{F}_q^\times} \chi(z)\chi(f(z))\\[5pt] &= 1 + \chi(c) + \#C(\mathbb{F}_q) + \sum_{z\in \mathbb{F}_q^\times} \chi(z) + \sum_{z\in \mathbb{F}_q^\times} \chi(z)\chi(f(z))\\[5pt] &= 1 + \chi(c) + \#C(\mathbb{F}_q) + \sum_{z\in \mathbb{F}_q^\times} \chi(z)\chi(f(z))\\[5pt] &= 1 + \chi(c) + \#C(\mathbb{F}_q) + \sum_{z\in \mathbb{F}_q} \chi(z)\chi(f(z))\,. \end{align*}
\begin{align*}\#D_0(\mathbb{F}_q)&= 2 + (1 + \chi(c)) + \sum_{z\in \mathbb{F}_q^\times} (1 + \chi(z))(1 + \chi(f(z))\\[5pt] &= 3 + \chi(c) + \sum_{z\in \mathbb{F}_q^\times} (1 + \chi(f(z))) + \sum_{z\in \mathbb{F}_q^\times} \chi(z) + \sum_{z\in \mathbb{F}_q^\times} \chi(z)\chi(f(z))\\[5pt] &= 1 + \chi(c) + \#C(\mathbb{F}_q) + \sum_{z\in \mathbb{F}_q^\times} \chi(z) + \sum_{z\in \mathbb{F}_q^\times} \chi(z)\chi(f(z))\\[5pt] &= 1 + \chi(c) + \#C(\mathbb{F}_q) + \sum_{z\in \mathbb{F}_q^\times} \chi(z)\chi(f(z))\\[5pt] &= 1 + \chi(c) + \#C(\mathbb{F}_q) + \sum_{z\in \mathbb{F}_q} \chi(z)\chi(f(z))\,. \end{align*}
If we define
![]() $N_0$
to be
$N_0$
to be
then
![]() $\#D_0(\mathbb{F}_q) = 1 + \chi(c) + \#C(\mathbb{F}_q) + N_0$
. Since
$\#D_0(\mathbb{F}_q) = 1 + \chi(c) + \#C(\mathbb{F}_q) + N_0$
. Since
![]() $D_0$
is hyperelliptic, it can have at most 2q rational points in addition to the
$D_0$
is hyperelliptic, it can have at most 2q rational points in addition to the
![]() $1 + \chi(c)$
points it has that lie over
$1 + \chi(c)$
points it has that lie over
![]() $x=0$
. Thus,
$x=0$
. Thus,
![]() $N_0\le 2q - \#C(\mathbb{F}_q).$
$N_0\le 2q - \#C(\mathbb{F}_q).$
Consider the sum, over all
![]() $a\in\mathbb{F}_q$
, of
$a\in\mathbb{F}_q$
, of
![]() $N_a$
. We have
$N_a$
. We have
 \begin{align*}\sum_{a\in\mathbb{F}_q} N_a&= \sum_{a\in \mathbb{F}_q} \sum_{z \in \mathbb{F}_q} \chi(z+a^2)\chi(f(z))\\[5pt] &= \sum_{z\in\mathbb{F}_q} \chi(f(z)) \sum_{a\in\mathbb{F}_q} \chi(z+a^2)\\[5pt] &= \sum_{z\in\mathbb{F}_q^\times} \chi(f(z)) \sum_{a\in\mathbb{F}_q} \chi(z+a^2),\end{align*}
\begin{align*}\sum_{a\in\mathbb{F}_q} N_a&= \sum_{a\in \mathbb{F}_q} \sum_{z \in \mathbb{F}_q} \chi(z+a^2)\chi(f(z))\\[5pt] &= \sum_{z\in\mathbb{F}_q} \chi(f(z)) \sum_{a\in\mathbb{F}_q} \chi(z+a^2)\\[5pt] &= \sum_{z\in\mathbb{F}_q^\times} \chi(f(z)) \sum_{a\in\mathbb{F}_q} \chi(z+a^2),\end{align*}
where the last equality follows because
![]() $\chi(f(0)) = 0$
. For nonzero
$\chi(f(0)) = 0$
. For nonzero
![]() $z\in\mathbb{F}_q$
, consider the genus-0 curve
$z\in\mathbb{F}_q$
, consider the genus-0 curve
![]() $X_z$
defined by
$X_z$
defined by
![]() $y^2 = x^2 + z$
. The curve
$y^2 = x^2 + z$
. The curve
![]() $X_z$
has two points at infinity, so arguing as before we find that
$X_z$
has two points at infinity, so arguing as before we find that
 \begin{align*}\#X_z(\mathbb{F}_q)&= 2 + \sum_{a\in\mathbb{F}_q} (1 + \chi(a^2 + z))\\[5pt] &= q + 2 + \sum_{a\in\mathbb{F}_q} \chi(a^2 + z)\,.\end{align*}
\begin{align*}\#X_z(\mathbb{F}_q)&= 2 + \sum_{a\in\mathbb{F}_q} (1 + \chi(a^2 + z))\\[5pt] &= q + 2 + \sum_{a\in\mathbb{F}_q} \chi(a^2 + z)\,.\end{align*}
Since
![]() $X_z$
has genus 0 and hence
$X_z$
has genus 0 and hence
![]() $1 + q$
rational points, we see that
$1 + q$
rational points, we see that
![]() $\sum_{a\in\mathbb{F}_q} \chi(a^2 + z) = -1$
when
$\sum_{a\in\mathbb{F}_q} \chi(a^2 + z) = -1$
when
![]() $z\ne 0$
. Therefore,
$z\ne 0$
. Therefore,
Suppose there were no nonzero a with
![]() $N_a\ge -1$
. Then we would have
$N_a\ge -1$
. Then we would have
which would imply
![]() $1 + q\le 2$
, a contradiction. Therefore there must be a nonzero a with
$1 + q\le 2$
, a contradiction. Therefore there must be a nonzero a with
![]() $N_a\ge -1$
, and for every such a the curve
$N_a\ge -1$
, and for every such a the curve
![]() $D_a$
satisfies the desired conditions.
$D_a$
satisfies the desired conditions.
Lemmas 4·3 and 4·5 give us the means to iterate a construction, but we still need base curves to start with. These will be provided by Lemmas 4·8 and 4·9. To prepare for the proofs of those lemmas, we need some background information on 2-isogenies and 2-isogeny volcanoes.
Let q be an odd prime power and let t be an integer, coprime to q, with
![]() $t^2<4q$
. Let
$t^2<4q$
. Let
![]() $\mathcal{C}_t$
be the isogeny class of ordinary elliptic curves over
$\mathcal{C}_t$
be the isogeny class of ordinary elliptic curves over
![]() $\mathbb{F}_q$
with trace t, and set
$\mathbb{F}_q$
with trace t, and set
![]() $\Delta\;:\!=\; t^2 - 4q < 0$
. Write
$\Delta\;:\!=\; t^2 - 4q < 0$
. Write
![]() $\Delta = F^2\Delta_0$
for a fundamental discriminant
$\Delta = F^2\Delta_0$
for a fundamental discriminant
![]() $\Delta_0$
. For every divisor f of F, there are elliptic curves in
$\Delta_0$
. For every divisor f of F, there are elliptic curves in
![]() $\mathcal{C}_t$
whose endomorphism rings are isomorphic to the quadratic order of discriminant
$\mathcal{C}_t$
whose endomorphism rings are isomorphic to the quadratic order of discriminant
![]() $f^2\Delta_0$
[
Reference WaterhouseWat69
, theorem 4·2, pp. 538--539].
$f^2\Delta_0$
[
Reference WaterhouseWat69
, theorem 4·2, pp. 538--539].
The height of the isogeny class
![]() $\mathcal{C}_t$
(more properly, the height of the 2-isogeny volcano associated to
$\mathcal{C}_t$
(more properly, the height of the 2-isogeny volcano associated to
![]() $\mathcal{C}_t$
) is equal to the 2-adic valuation of the conductor F. If E is an elliptic curve in
$\mathcal{C}_t$
) is equal to the 2-adic valuation of the conductor F. If E is an elliptic curve in
![]() $\mathcal{C}_t$
whose endomorphism ring has discriminant
$\mathcal{C}_t$
whose endomorphism ring has discriminant
![]() $f^2\Delta_0$
, then the level of E is the 2-adic valuation of f. (This is the terminology of [
Reference Fouquet and MorainFM02
]; Kohel used different terminology in his thesis [
Reference KohelKoh96
], which introduced these concepts.) We see that
$f^2\Delta_0$
, then the level of E is the 2-adic valuation of f. (This is the terminology of [
Reference Fouquet and MorainFM02
]; Kohel used different terminology in his thesis [
Reference KohelKoh96
], which introduced these concepts.) We see that
![]() $\mathcal{C}_t$
contains elliptic curves of every level from 0 to the height of
$\mathcal{C}_t$
contains elliptic curves of every level from 0 to the height of
![]() $\mathcal{C}_t$
.
$\mathcal{C}_t$
.
Lemma 4·6.
Let
![]() $\mathcal{C}_t$
be an ordinary isogeny class of trace t and discriminant
$\mathcal{C}_t$
be an ordinary isogeny class of trace t and discriminant
![]() $\Delta= F^2\Delta_0$
as above, and suppose
$\Delta= F^2\Delta_0$
as above, and suppose
![]() $\mathcal{C}_t$
has height
$\mathcal{C}_t$
has height
![]() $h>0$
. Then:
$h>0$
. Then:
-
(i) every elliptic curve in
 $\mathcal{C}_t$
of level h has exactly one rational point of order 2, and the image of the corresponding 2-isogeny is an elliptic curve of level
$\mathcal{C}_t$
of level h has exactly one rational point of order 2, and the image of the corresponding 2-isogeny is an elliptic curve of level
 $h-1$
;
$h-1$
; -
(ii) every elliptic curve in
 $\mathcal{C}_t$
of level
$\mathcal{C}_t$
of level
 $\ell$
with
$\ell$
with
 $0 < \ell < h$
has exactly three rational points of order 2. For two of these points, the image of the corresponding 2-isogeny is a curve of level
$0 < \ell < h$
has exactly three rational points of order 2. For two of these points, the image of the corresponding 2-isogeny is a curve of level
 $\ell+1$
, and for the third the image is an elliptic curve of level
$\ell+1$
, and for the third the image is an elliptic curve of level
 $\ell-1$
;
$\ell-1$
; -
(iii) every elliptic curve in
 $\mathcal{C}_t$
of level 0 has exactly three rational points of order 2. The images of the corresponding 2-isogenies are curves of level 0 or 1, and the number of points giving rise to a curve of level 0 is equal to 2, 1, or 0, corresponding to whether
$\mathcal{C}_t$
of level 0 has exactly three rational points of order 2. The images of the corresponding 2-isogenies are curves of level 0 or 1, and the number of points giving rise to a curve of level 0 is equal to 2, 1, or 0, corresponding to whether
 $\Delta_0\equiv 1\bmod 8$
,
$\Delta_0\equiv 1\bmod 8$
,
 $\Delta_0\equiv0 \bmod 4$
, or
$\Delta_0\equiv0 \bmod 4$
, or
 $\Delta_0\equiv 5\bmod 8$
.
$\Delta_0\equiv 5\bmod 8$
.
Proof. This follows immediately from [ Reference Fouquet and MorainFM02 , theorem 2·1, p. 278] or [ Reference KohelKoh96 , proposition 23, p. 54].
Lemma 4·7.
Let q be an odd prime power and let
![]() $E\colon y^2 = (x-a)(x-b)(x-c)$
be an elliptic curve over
$E\colon y^2 = (x-a)(x-b)(x-c)$
be an elliptic curve over
![]() $\mathbb{F}_q$
with all of its 2-torsion rational. Let
$\mathbb{F}_q$
with all of its 2-torsion rational. Let
![]() $\varphi\colon E\to F$
be the 2-isogeny with kernel generated by the point (a,0) on E. Then all of the 2-torsion of F is rational if and only if
$\varphi\colon E\to F$
be the 2-isogeny with kernel generated by the point (a,0) on E. Then all of the 2-torsion of F is rational if and only if
![]() $(a-b)(a-c)$
is a square.
$(a-b)(a-c)$
is a square.
Proof. By shifting x-coordinates on E by a, we see that it suffices to prove the statement when
![]() $a = 0$
. Using [
Reference SilvermanSil09
, example 4·5, p. 70], for example, we find that one model for F is given by
$a = 0$
. Using [
Reference SilvermanSil09
, example 4·5, p. 70], for example, we find that one model for F is given by
![]() $y^2 = x^3 + 2(b+c)x^2 + (b-c)^2x$
. The 2-torsion of F is all rational if and only if the quadratic
$y^2 = x^3 + 2(b+c)x^2 + (b-c)^2x$
. The 2-torsion of F is all rational if and only if the quadratic
![]() $x^2 + 2(b+c)x + (b-c)^2$
splits, which happens if and only if its discriminant 16bc is a square.
$x^2 + 2(b+c)x + (b-c)^2$
splits, which happens if and only if its discriminant 16bc is a square.
Lemma 4·8.
Let q be an odd prime power. Then there is a curve
![]() $C/\mathbb{F}_q$
of genus 2 with exactly two rational Weierstrass points such that
$C/\mathbb{F}_q$
of genus 2 with exactly two rational Weierstrass points such that
 \[\#C(\mathbb{F}_q) > \begin{cases} 1 + q + 4\sqrt{q} - 5 & \text{if $q<512$};\\[5pt] 1 + q + 4\sqrt{q} - 32 & \text{if $q>512$}.\\[5pt] \end{cases}\]
\[\#C(\mathbb{F}_q) > \begin{cases} 1 + q + 4\sqrt{q} - 5 & \text{if $q<512$};\\[5pt] 1 + q + 4\sqrt{q} - 32 & \text{if $q>512$}.\\[5pt] \end{cases}\]
Proof. For
![]() $q<512$
we find examples of such curves by computer search; a list of examples is included with the ancillary files included with the arXiv version of this paper. Thus we may assume that
$q<512$
we find examples of such curves by computer search; a list of examples is included with the ancillary files included with the arXiv version of this paper. Thus we may assume that
![]() $q > 512$
.
$q > 512$
.
First consider the case where
![]() $q\equiv 3\bmod 4$
. Let t be the largest integer such that
$q\equiv 3\bmod 4$
. Let t be the largest integer such that
![]() $t\equiv q + 1\bmod 8$
and
$t\equiv q + 1\bmod 8$
and
![]() $(t,q) = 1$
and
$(t,q) = 1$
and
![]() $t^2 \le 4q$
, so that
$t^2 \le 4q$
, so that
![]() $t>2\sqrt{q} - 16>0$
. Set
$t>2\sqrt{q} - 16>0$
. Set
![]() $\Delta \;:\!=\; t^2 - 4q$
and write
$\Delta \;:\!=\; t^2 - 4q$
and write
![]() $\Delta = F^2\Delta_0$
for a fundamental discriminant
$\Delta = F^2\Delta_0$
for a fundamental discriminant
![]() $\Delta_0$
. We note that
$\Delta_0$
. We note that
![]() $\Delta \equiv 4\bmod 32$
, so that
$\Delta \equiv 4\bmod 32$
, so that
![]() $F\equiv 2\bmod 4$
and
$F\equiv 2\bmod 4$
and
![]() $\Delta_0\equiv 1\bmod 8$
. If we let
$\Delta_0\equiv 1\bmod 8$
. If we let
![]() $\mathcal{C}_{-t}$
be the isogeny class of elliptic curves of trace
$\mathcal{C}_{-t}$
be the isogeny class of elliptic curves of trace
![]() $-t$
over
$-t$
over
![]() $\mathbb{F}_q$
, then
$\mathbb{F}_q$
, then
![]() $\mathcal{C}_{-t}$
has height 1.
$\mathcal{C}_{-t}$
has height 1.
Let E be an elliptic curve in
![]() $\mathcal{C}_{-t}$
of level 0. By Lemma 4·6, E has two rational 2-isogenies to elliptic curves of level 0 and one rational 2-isogeny to an elliptic curve E
′ of level 1. Write E as
$\mathcal{C}_{-t}$
of level 0. By Lemma 4·6, E has two rational 2-isogenies to elliptic curves of level 0 and one rational 2-isogeny to an elliptic curve E
′ of level 1. Write E as
![]() $y^2 = x(x-a)(x-b)$
, with coordinates chosen so that the 2-isogeny from E to E
′ has kernel generated by (0,0). Since E
′ does not have all of its 2-torsion rational, Lemma 4·7 shows that ab is not a square; on the other hand, since the other curves 2-isogenous to E do have their 2-torsion rational, we find that
$y^2 = x(x-a)(x-b)$
, with coordinates chosen so that the 2-isogeny from E to E
′ has kernel generated by (0,0). Since E
′ does not have all of its 2-torsion rational, Lemma 4·7 shows that ab is not a square; on the other hand, since the other curves 2-isogenous to E do have their 2-torsion rational, we find that
![]() $a(a-b)$
and
$a(a-b)$
and
![]() $b(b-a)$
are both squares.
$b(b-a)$
are both squares.
Define elements
![]() $\alpha_i$
and
$\alpha_i$
and
![]() $\beta_i$
of
$\beta_i$
of
![]() $\mathbb{F}_q$
, for
$\mathbb{F}_q$
, for
![]() $i=1,2,3$
, by
$i=1,2,3$
, by
Let
![]() $\psi\colon E[2]\to E[2]$
be the isomorphism that takes
$\psi\colon E[2]\to E[2]$
be the isomorphism that takes
![]() $(\alpha_i,0)$
to
$(\alpha_i,0)$
to
![]() $(\beta_i,0)$
for each i. Since the discriminant of the endomorphism ring of E is congruent to
$(\beta_i,0)$
for each i. Since the discriminant of the endomorphism ring of E is congruent to
![]() $1\bmod 8$
, the curve E has no nontrivial automorphisms, and
$1\bmod 8$
, the curve E has no nontrivial automorphisms, and
![]() $\psi$
is not the restriction to E[2] of an automorphism of E. Therefore, from [
Reference Howe, Leprévost and PoonenHLP00
, propositions 3 and 4, p. 324] we obtain a curve C of genus 2 whose Jacobian is isogenous to
$\psi$
is not the restriction to E[2] of an automorphism of E. Therefore, from [
Reference Howe, Leprévost and PoonenHLP00
, propositions 3 and 4, p. 324] we obtain a curve C of genus 2 whose Jacobian is isogenous to
![]() $E^2$
, and the formulas in the cited results give us a model for C. In this case, we find that C is given by
$E^2$
, and the formulas in the cited results give us a model for C. In this case, we find that C is given by
![]() $y^2 = h$
with
$y^2 = h$
with
Now, since ab and
![]() $-1$
are both nonsquare, it follows that
$-1$
are both nonsquare, it follows that
![]() $-b/a$
is a square, so the first quadratic factor in h splits. On the other hand, since
$-b/a$
is a square, so the first quadratic factor in h splits. On the other hand, since
![]() $b(b-a)$
is a square, we see that
$b(b-a)$
is a square, we see that
![]() $(a-b)/b$
is not a square, so the second quadratic factor of h is irreducible. Likewise, the third quadratic factor is irreducible. Therefore, C has exactly two rational Weierstrass points.
$(a-b)/b$
is not a square, so the second quadratic factor of h is irreducible. Likewise, the third quadratic factor is irreducible. Therefore, C has exactly two rational Weierstrass points.
Since the Jacobian of C is isogenous to
![]() $E^2$
, we have
$E^2$
, we have
![]() $\#C(\mathbb{F}_q) = 1 + q + 2t > 1 + q + 4\sqrt{q} - 32.$
$\#C(\mathbb{F}_q) = 1 + q + 2t > 1 + q + 4\sqrt{q} - 32.$
Now we turn to the case where
![]() $q \equiv 1 \bmod 4$
. Let t be the largest integer such that
$q \equiv 1 \bmod 4$
. Let t be the largest integer such that
![]() $t\equiv 2\bmod 4$
and
$t\equiv 2\bmod 4$
and
![]() $(t,q) = 1$
and
$(t,q) = 1$
and
![]() $t^2 \le 4q$
, so that
$t^2 \le 4q$
, so that
![]() $t>2\sqrt{q} - 8 > 0$
. Let
$t>2\sqrt{q} - 8 > 0$
. Let
![]() $\mathcal{C}_{-t}$
be the isogeny class of ordinary elliptic curves over
$\mathcal{C}_{-t}$
be the isogeny class of ordinary elliptic curves over
![]() $\mathbb{F}_q$
with trace
$\mathbb{F}_q$
with trace
![]() $-t$
, set
$-t$
, set
![]() $\Delta \;:\!=\; t^2 - 4q$
, and write
$\Delta \;:\!=\; t^2 - 4q$
, and write
![]() $\Delta = F^2\Delta_0$
for a fundamental discriminant
$\Delta = F^2\Delta_0$
for a fundamental discriminant
![]() $\Delta_0$
. We note that
$\Delta_0$
. We note that
![]() $\Delta \equiv 0\bmod 16$
, so that either the height h of
$\Delta \equiv 0\bmod 16$
, so that either the height h of
![]() $\mathcal{C}_{-t}$
is at least 2, or
$\mathcal{C}_{-t}$
is at least 2, or
![]() $h=1$
and
$h=1$
and
![]() $\Delta_0 \equiv 0\bmod 4$
.
$\Delta_0 \equiv 0\bmod 4$
.
Let E be an elliptic curve in
![]() $\mathcal{C}_{-t}$
of level
$\mathcal{C}_{-t}$
of level
![]() $h-1$
. Lemma 4·6 shows that if
$h-1$
. Lemma 4·6 shows that if
![]() $h\ge 2$
, then E has two 2-isogenies to elliptic curves of level h and one to an elliptic curve of level
$h\ge 2$
, then E has two 2-isogenies to elliptic curves of level h and one to an elliptic curve of level
![]() $h-2$
. The curves of level h have only one rational point of order 2, while the curve of level
$h-2$
. The curves of level h have only one rational point of order 2, while the curve of level
![]() $h-2$
has three rational points of order 2. On the other hand, if
$h-2$
has three rational points of order 2. On the other hand, if
![]() $h=1$
and
$h=1$
and
![]() $\Delta_0\equiv0\bmod 4$
then E has two 2-isogenies to elliptic curves of level 1 and one to an elliptic curve of level 0. Again, the curves of level 1 have only one rational point of order 2, while the curve of level 0 has three rational points of order 2.
$\Delta_0\equiv0\bmod 4$
then E has two 2-isogenies to elliptic curves of level 1 and one to an elliptic curve of level 0. Again, the curves of level 1 have only one rational point of order 2, while the curve of level 0 has three rational points of order 2.
We see that in every case, E can be written in the form
![]() $y^2 = x(x-a)(x-b)$
where ab is a square and where
$y^2 = x(x-a)(x-b)$
where ab is a square and where
![]() $(a-b)/a$
and
$(a-b)/a$
and
![]() $(b-a)/b$
are both nonsquares. Taking
$(b-a)/b$
are both nonsquares. Taking
![]() $\alpha_i$
and
$\alpha_i$
and
![]() $\beta_i$
as before, we find that the curve C given by
$\beta_i$
as before, we find that the curve C given by
![]() $y^2 = h$
, with
$y^2 = h$
, with
has Jacobian isogenous to
![]() $E^2$
. We again find that the first quadratic factor splits and the other two are irreducible, so once again C has exactly two rational Weierstrass points. We also once again have
$E^2$
. We again find that the first quadratic factor splits and the other two are irreducible, so once again C has exactly two rational Weierstrass points. We also once again have
![]() $\#C(\mathbb{F}_q) = 1 + q + 2t.$
$\#C(\mathbb{F}_q) = 1 + q + 2t.$
Thus, for every odd prime power q we have shown that there is a curve of genus 2 over
![]() $\mathbb{F}_q$
with exactly two rational Weierstrass points and with
$\mathbb{F}_q$
with exactly two rational Weierstrass points and with
![]() $\#C(\mathbb{F}_q) > 1 + q + 4\sqrt{q} - 32.$
$\#C(\mathbb{F}_q) > 1 + q + 4\sqrt{q} - 32.$
Lemma 4·9.
Let q be an odd prime power. Then there is a hyperelliptic curve
![]() $C/\mathbb{F}_q$
of genus 3 with exactly two rational Weierstrass points and with
$C/\mathbb{F}_q$
of genus 3 with exactly two rational Weierstrass points and with
 \[\#C(\mathbb{F}_q) > \begin{cases} 1 + q + 4\sqrt{q} - 5 & \text{if $q<512$};\\[5pt] 1 + q + 4\sqrt{q} - 32 & \text{if $q>512$}.\\[5pt] \end{cases}\]
\[\#C(\mathbb{F}_q) > \begin{cases} 1 + q + 4\sqrt{q} - 5 & \text{if $q<512$};\\[5pt] 1 + q + 4\sqrt{q} - 32 & \text{if $q>512$}.\\[5pt] \end{cases}\]
Proof. The statement for
![]() $q<512$
is verified by computer search; a list of examples of such curves can be found in the ancillary files included with the arXiv version of this paper. We assume now that
$q<512$
is verified by computer search; a list of examples of such curves can be found in the ancillary files included with the arXiv version of this paper. We assume now that
![]() $q>512$
.
$q>512$
.
First consider the case where
![]() $q\equiv 3\bmod 4$
. As in the proof of Lemma 4·8, we let t be the largest integer such that
$q\equiv 3\bmod 4$
. As in the proof of Lemma 4·8, we let t be the largest integer such that
![]() $t\equiv q + 1\bmod 8$
and
$t\equiv q + 1\bmod 8$
and
![]() $(t,q) = 1$
and
$(t,q) = 1$
and
![]() $t^2 \le 4q$
, so that
$t^2 \le 4q$
, so that
![]() $t>2\sqrt{q} - 16>0$
. We see that
$t>2\sqrt{q} - 16>0$
. We see that
![]() $\Delta\;:\!=\; t^2 - 4q$
can be written
$\Delta\;:\!=\; t^2 - 4q$
can be written
![]() $F^2\Delta_0$
for a fundamental discriminant
$F^2\Delta_0$
for a fundamental discriminant
![]() $\Delta_0$
that is congruent to 1 modulo 8 and a conductor F that is congruent to 2 modulo 4. If we let
$\Delta_0$
that is congruent to 1 modulo 8 and a conductor F that is congruent to 2 modulo 4. If we let
![]() $\mathcal{C}_{-t}$
be the isogeny class of elliptic curves of trace
$\mathcal{C}_{-t}$
be the isogeny class of elliptic curves of trace
![]() $-t$
over
$-t$
over
![]() $\mathbb{F}_q$
, then
$\mathbb{F}_q$
, then
![]() $\mathcal{C}_{-t}$
has height 1.
$\mathcal{C}_{-t}$
has height 1.
Let E be an elliptic curve in
![]() $\mathcal{C}_{-t}$
of level 0. Lemma 4·6 shows that E has two rational 2-isogenies to elliptic curves of level 0. Let E
′ be one of these curves, and write E as
$\mathcal{C}_{-t}$
of level 0. Lemma 4·6 shows that E has two rational 2-isogenies to elliptic curves of level 0. Let E
′ be one of these curves, and write E as
![]() $y^2 = x(x-a)(x-b)$
, with coordinates chosen so that the 2-isogeny from E to E
′ has kernel generated by (0,0). Since E
′ is of level 0 it has all of its 2-torsion rational, so Lemma 4·7 shows that ab is a square; therefore
$y^2 = x(x-a)(x-b)$
, with coordinates chosen so that the 2-isogeny from E to E
′ has kernel generated by (0,0). Since E
′ is of level 0 it has all of its 2-torsion rational, so Lemma 4·7 shows that ab is a square; therefore
![]() $b/a$
is also a square, say
$b/a$
is also a square, say
![]() $b/a = c^2$
.
$b/a = c^2$
.
Define elements
![]() $\alpha_i$
and
$\alpha_i$
and
![]() $\beta_i$
of
$\beta_i$
of
![]() $\mathbb{F}_q$
, for
$\mathbb{F}_q$
, for
![]() $i=1,2,3$
, by
$i=1,2,3$
, by
and let
![]() $\psi\colon E[2]\to E[2]$
be the isomorphism that takes
$\psi\colon E[2]\to E[2]$
be the isomorphism that takes
![]() $(\alpha_i,0)$
to
$(\alpha_i,0)$
to
![]() $(\beta_i,0)$
for each i. Since the discriminant of the endomorphism ring of E is congruent to
$(\beta_i,0)$
for each i. Since the discriminant of the endomorphism ring of E is congruent to
![]() $1\bmod 8$
, the curve E has no nontrivial automorphisms, and
$1\bmod 8$
, the curve E has no nontrivial automorphisms, and
![]() $\psi$
is not the restriction to E[2] of an automorphism of E. Once again we use [
Reference Howe, Leprévost and PoonenHLP00
, propositions 3 and 4, p. 324] to show that there is a genus-2 curve C whose Jacobian is (2,2)-isogenous to
$\psi$
is not the restriction to E[2] of an automorphism of E. Once again we use [
Reference Howe, Leprévost and PoonenHLP00
, propositions 3 and 4, p. 324] to show that there is a genus-2 curve C whose Jacobian is (2,2)-isogenous to
![]() $E^2$
, and we find that one model for such a C is given by
$E^2$
, and we find that one model for such a C is given by
![]() $y^2 = h$
with
$y^2 = h$
with
Since the Jacobian of C is isogenous to
![]() $E^2$
, we have
$E^2$
, we have
![]() $\#C(\mathbb{F}_q) = 1 + q + 2t > 1 + q + 4\sqrt{q} - 32.$
$\#C(\mathbb{F}_q) = 1 + q + 2t > 1 + q + 4\sqrt{q} - 32.$
Now we replace x with
![]() $(2c^2x + 1-c^2)/(2cx + c^3 - c)$
and scale y appropriately to find that C can also be written
$(2c^2x + 1-c^2)/(2cx + c^3 - c)$
and scale y appropriately to find that C can also be written
![]() $y^2 = f$
, where
$y^2 = f$
, where
Note that the quadratic factor is irreducible.
Now, as in the proof of Lemma 4·3, we consider two double covers of C. Let
![]() $g = f/x$
, let n be a nonsquare element of
$g = f/x$
, let n be a nonsquare element of
![]() $\mathbb{F}_q$
, let D be the curve
$\mathbb{F}_q$
, let D be the curve
![]() $y^2 = g(x^2)$
, and let D
′ be the curve
$y^2 = g(x^2)$
, and let D
′ be the curve
![]() $y^2 = g(nx^2)$
. The curves D and D
′ are both double covers of C: The map
$y^2 = g(nx^2)$
. The curves D and D
′ are both double covers of C: The map
![]() $(x,y) \mapsto (x^2,xy)$
sends D to C, and the map
$(x,y) \mapsto (x^2,xy)$
sends D to C, and the map
![]() $(x,y) \mapsto (nx^2,xy)$
sends D
′ to C. The two covers are quadratic twists of one another, so we have
$(x,y) \mapsto (nx^2,xy)$
sends D
′ to C. The two covers are quadratic twists of one another, so we have
![]() $\#D(\mathbb{F}_q) + \#D'(\mathbb{F}_q) = 2\#C(\mathbb{F}_q)$
, so at least one of D and D
′ has at least as many points as C. Also, the two curves are both hyperelliptic of genus 3. Furthermore, the rational Weierstrass point (1,0) of C splits into two rational Weierstrass points of D while the rational Weierstrass point lying over
$\#D(\mathbb{F}_q) + \#D'(\mathbb{F}_q) = 2\#C(\mathbb{F}_q)$
, so at least one of D and D
′ has at least as many points as C. Also, the two curves are both hyperelliptic of genus 3. Furthermore, the rational Weierstrass point (1,0) of C splits into two rational Weierstrass points of D while the rational Weierstrass point lying over
![]() $x = -(c^2 - 1)^2/(4c^2)$
does not, because
$x = -(c^2 - 1)^2/(4c^2)$
does not, because
![]() $-1$
is not a square, whereas for D
′ the splitting behaviour of these two points is reversed. Thus, both D and D
′ have exactly two rational Weierstrass points.
$-1$
is not a square, whereas for D
′ the splitting behaviour of these two points is reversed. Thus, both D and D
′ have exactly two rational Weierstrass points.
We have shown that there is a hyperelliptic curve over
![]() $\mathbb{F}_q$
of genus 3 with exactly two rational Weierstrass points and with more than
$\mathbb{F}_q$
of genus 3 with exactly two rational Weierstrass points and with more than
![]() $1 + q + 4\sqrt{q} - 32$
rational points.
$1 + q + 4\sqrt{q} - 32$
rational points.
Now consider the case
![]() $q\equiv 1\bmod 4$
. If
$q\equiv 1\bmod 4$
. If
![]() $q\equiv 1\bmod 16$
or
$q\equiv 1\bmod 16$
or
![]() $q\equiv 13\bmod 16$
, let t be the largest integer congruent to 2 or 14 modulo 16 that is coprime to q and such that
$q\equiv 13\bmod 16$
, let t be the largest integer congruent to 2 or 14 modulo 16 that is coprime to q and such that
![]() $t^2<4q$
; if
$t^2<4q$
; if
![]() $q\equiv 5\bmod 16$
or
$q\equiv 5\bmod 16$
or
![]() $q\equiv 9\bmod 16$
, let t be the largest integer congruent to 6 or 10 modulo 16 that is coprime to q and such that
$q\equiv 9\bmod 16$
, let t be the largest integer congruent to 6 or 10 modulo 16 that is coprime to q and such that
![]() $t^2<4q$
. In both cases we have
$t^2<4q$
. In both cases we have
![]() $t>2\sqrt{q}-16$
.
$t>2\sqrt{q}-16$
.
Let
![]() $\Delta \;:\!=\; t^2 - 4q$
and write
$\Delta \;:\!=\; t^2 - 4q$
and write
![]() $\Delta = F^2\Delta_0$
for a fundamental discriminant
$\Delta = F^2\Delta_0$
for a fundamental discriminant
![]() $\Delta_0$
. Our choice of t guarantees that
$\Delta_0$
. Our choice of t guarantees that
![]() $\Delta\equiv 0\bmod 64$
, so
$\Delta\equiv 0\bmod 64$
, so
![]() $F\equiv 0\bmod 4$
. If we let
$F\equiv 0\bmod 4$
. If we let
![]() $\mathcal{C}_{-t}$
be the isogeny class of elliptic curves of trace
$\mathcal{C}_{-t}$
be the isogeny class of elliptic curves of trace
![]() $-t$
over
$-t$
over
![]() $\mathbb{F}_q$
, then the height h of
$\mathbb{F}_q$
, then the height h of
![]() $\mathcal{C}_{-t}$
is at least 2.
$\mathcal{C}_{-t}$
is at least 2.
Let E be an elliptic curve in
![]() $\mathcal{C}_{-t}$
of level
$\mathcal{C}_{-t}$
of level
![]() $h-2$
, and let E
′ be an elliptic curve of height
$h-2$
, and let E
′ be an elliptic curve of height
![]() $h-1$
that is 2-isogenous to E. Write E as
$h-1$
that is 2-isogenous to E. Write E as
![]() $y^2 = x(x-a)(x-b)$
so that the kernel of the 2-isogeny to E
′ contains the point (0,0). Since E
′ has all of its 2-torsion rational, Lemma 4·7 shows that ab is a square, so we can write
$y^2 = x(x-a)(x-b)$
so that the kernel of the 2-isogeny to E
′ contains the point (0,0). Since E
′ has all of its 2-torsion rational, Lemma 4·7 shows that ab is a square, so we can write
![]() $b = ac^2$
for some
$b = ac^2$
for some
![]() $c\in\mathbb{F}_q$
. Then the fact that the other two curves 2-isogenous to E have all of their 2-torsion rational implies that
$c\in\mathbb{F}_q$
. Then the fact that the other two curves 2-isogenous to E have all of their 2-torsion rational implies that
![]() $a^2(1-c^2)$
and
$a^2(1-c^2)$
and
![]() $a^2c^2(c^2-1)$
are squares, so
$a^2c^2(c^2-1)$
are squares, so
![]() $c^2 - 1$
is a square.
$c^2 - 1$
is a square.
We compute that one model for E ′ is given by
Here, the isogeny
![]() $E'\to E$
corresponds to the 2-torsion point (0,0). The other two 2-isogenous take E
′ to curves of level h, which each have exactly one rational point of order 2, so Lemma 4·7 tells us that the two values
$E'\to E$
corresponds to the 2-torsion point (0,0). The other two 2-isogenous take E
′ to curves of level h, which each have exactly one rational point of order 2, so Lemma 4·7 tells us that the two values
![]() $4a^2c(c+1)^2$
and
$4a^2c(c+1)^2$
and
![]() $-4a^2c(c-1)^2$
are not squares. This shows that c is not a square.
$-4a^2c(c-1)^2$
are not squares. This shows that c is not a square.
Now we use the formulae from [
Reference Howe, Leprévost and PoonenHLP00
, proposition 4, p. 324] to construct a curve of genus 2 whose Jacobian is (2,2)-isogenous to
![]() $E\times E'$
. In particular, we take
$E\times E'$
. In particular, we take
in [
Reference Howe, Leprévost and PoonenHLP00
, proposition 4, p. 324] and we find that the resulting curve C is given by
![]() $y^2 = h$
, where
$y^2 = h$
, where
Since the Jacobian of C is isogenous to
![]() $E^2$
, we have
$E^2$
, we have
![]() $\#C(\mathbb{F}_q) = 1 + q + 2t > 1 + q + 4\sqrt{q} - 32.$
$\#C(\mathbb{F}_q) = 1 + q + 2t > 1 + q + 4\sqrt{q} - 32.$
The first of the quadratic factors in the above expression for h is irreducible, because
![]() $c^2-1$
is a square but c is not. The other two quadratic factors split, and if we let i denote a square root of
$c^2-1$
is a square but c is not. The other two quadratic factors split, and if we let i denote a square root of
![]() $-1$
in
$-1$
in
![]() $\mathbb{F}_q$
, then the roots of h are
$\mathbb{F}_q$
, then the roots of h are
If we replace x with
and rescale y appropriately, we find that C can also be written as
![]() $y^2 = f$
, where
$y^2 = f$
, where
Note that the quadratic factor is irreducible, and that the root
![]() $r\;:\!=\; 4 c (c^2 - 1)/(c^2 + 2c - 1)^2$
is not a square, because c is not a square while
$r\;:\!=\; 4 c (c^2 - 1)/(c^2 + 2c - 1)^2$
is not a square, because c is not a square while
![]() $c^2 - 1$
is.
$c^2 - 1$
is.
Let
![]() $g = f/x$
, let n be a nonsquare element of
$g = f/x$
, let n be a nonsquare element of
![]() $\mathbb{F}_q$
, let D be the curve
$\mathbb{F}_q$
, let D be the curve
![]() $y^2 = g(x^2)$
, and let D
′ be the curve
$y^2 = g(x^2)$
, and let D
′ be the curve
![]() $y^2 = g(nx^2)$
. As before, the curves D and D
′ are both double covers of C and the two covers are quadratic twists of one another, so at least one of D and D
′ has at least as many points as C. The two curves are both hyperelliptic of genus 3. And finally, the rational Weierstrass point (1,0) of C splits into two rational Weierstrass points of D while the rational Weierstrass point (r,0) does not, whereas for D
′ the splitting behaviour of these two points is reversed. Thus, both D and D
′ have exactly two rational Weierstrass points.
$y^2 = g(nx^2)$
. As before, the curves D and D
′ are both double covers of C and the two covers are quadratic twists of one another, so at least one of D and D
′ has at least as many points as C. The two curves are both hyperelliptic of genus 3. And finally, the rational Weierstrass point (1,0) of C splits into two rational Weierstrass points of D while the rational Weierstrass point (r,0) does not, whereas for D
′ the splitting behaviour of these two points is reversed. Thus, both D and D
′ have exactly two rational Weierstrass points.
We have shown that there is a hyperelliptic curve of genus 3 over
![]() $\mathbb{F}_q$
with exactly two rational Weierstrass points and with more than
$\mathbb{F}_q$
with exactly two rational Weierstrass points and with more than
![]() $1 + q + 4\sqrt{q} - 32$
rational points.
$1 + q + 4\sqrt{q} - 32$
rational points.
With all of these preparatory results at hand, the proof of Theorem 4·1 for odd q is very short.
Proof of Theorem 4·1(i). We prove the result by induction on g. The statement is true for
![]() $g=2$
and
$g=2$
and
![]() $g=3$
by Lemmas 4·8 and 4·9. Now suppose Theorem 4·1(i) holds for all g less than some integer
$g=3$
by Lemmas 4·8 and 4·9. Now suppose Theorem 4·1(i) holds for all g less than some integer
![]() $G>3$
. We will show it also holds when
$G>3$
. We will show it also holds when
![]() $g = G$
.
$g = G$
.
For convenience’s sake, let us set
![]() $c_q = 5$
if
$c_q = 5$
if
![]() $q<512$
and
$q<512$
and
![]() $c_q=32$
if
$c_q=32$
if
![]() $q>512$
. Set
$q>512$
. Set
![]() $h = \lfloor G/2\rfloor$
. Then
$h = \lfloor G/2\rfloor$
. Then
![]() $h>1$
, and we may apply Theorem 4·1(i) to show that for every q, there is a hyperelliptic curve
$h>1$
, and we may apply Theorem 4·1(i) to show that for every q, there is a hyperelliptic curve
![]() $C/\mathbb{F}_q$
of genus h with exactly two rational Weierstrass points and with
$C/\mathbb{F}_q$
of genus h with exactly two rational Weierstrass points and with
![]() $\#C(\mathbb{F}_q) > 1 + q + 4\sqrt{q} - c_q$
.
$\#C(\mathbb{F}_q) > 1 + q + 4\sqrt{q} - c_q$
.
If G is odd, we apply Lemma 4·3 to the curve C and find that there is a hyperelliptic curve D of genus
![]() $2h+1 = G$
with exactly two rational Weierstrass points and with
$2h+1 = G$
with exactly two rational Weierstrass points and with
![]() $\#D(\mathbb{F}_q)\ge \#C(\mathbb{F}_q)$
.
$\#D(\mathbb{F}_q)\ge \#C(\mathbb{F}_q)$
.
If G is even, we apply Lemma 4·5 to the curve C and find that there is a hyperelliptic curve D of genus
![]() $2h = G$
with exactly two rational Weierstrass points and with
$2h = G$
with exactly two rational Weierstrass points and with
![]() $\#D(\mathbb{F}_q)\ge \#C(\mathbb{F}_q)$
.
$\#D(\mathbb{F}_q)\ge \#C(\mathbb{F}_q)$
.
4·2. Characteristic 2
In this section, we prove Theorem 4·1 for finite fields of characteristic 2. The spirit of the proof is very similar to the odd characteristic case, but the switch to Artin–Schreier extensions instead of Kummer extensions requires a few technical modifications. We begin with some basic observations about hyperelliptic curves in characteristic 2.
If q is a power of 2 and C is a hyperelliptic curve over
![]() $\mathbb{F}_q$
, then C has a model of the form
$\mathbb{F}_q$
, then C has a model of the form
![]() $y^2 + y = f$
for a rational function
$y^2 + y = f$
for a rational function
![]() $f\in\mathbb{F}_q(x)$
. Replacing y with
$f\in\mathbb{F}_q(x)$
. Replacing y with
![]() $y + u$
for a rational function
$y + u$
for a rational function
![]() $u\in\mathbb{F}_q(x)$
turns the equation for C into
$u\in\mathbb{F}_q(x)$
turns the equation for C into
![]() $y^2 + y = f + u^2 + u$
, and by modifying f in this way we can assume that all of the poles of f, including the pole at
$y^2 + y = f + u^2 + u$
, and by modifying f in this way we can assume that all of the poles of f, including the pole at
![]() $\infty$
, have odd order. Suppose f has r poles, with orders
$\infty$
, have odd order. Suppose f has r poles, with orders
![]() $d_1,\ldots,d_r$
. Then the Weierstrass points of C are precisely the points lying over the poles of f in
$d_1,\ldots,d_r$
. Then the Weierstrass points of C are precisely the points lying over the poles of f in
![]() $\mathbb{P}^1$
, and [
Reference StichtenothSti09
, proposition 3·7·8, p.127] shows that the genus g of C is given by
$\mathbb{P}^1$
, and [
Reference StichtenothSti09
, proposition 3·7·8, p.127] shows that the genus g of C is given by
Lemma 4·10.
Let q be a power of 2 and let
![]() $C/\mathbb{F}_q$
be a hyperelliptic curve of genus g, so that C has a model
$C/\mathbb{F}_q$
be a hyperelliptic curve of genus g, so that C has a model
![]() $y^2 + y = f$
for a rational function
$y^2 + y = f$
for a rational function
![]() $f\in\mathbb{F}_q(x)$
all of whose poles have odd order. Given
$f\in\mathbb{F}_q(x)$
all of whose poles have odd order. Given
![]() $a\in\mathbb{F}_q^\times$
and
$a\in\mathbb{F}_q^\times$
and
![]() $b\in\mathbb{F}_q$
, let
$b\in\mathbb{F}_q$
, let
![]() $h = f((x^2+x+b)/a)$
and let D be the curve defined by
$h = f((x^2+x+b)/a)$
and let D be the curve defined by
![]() $y^2 + y = h$
. Then:
$y^2 + y = h$
. Then:
-
(i) if f has no pole at infinity, the genus of D is
 $2g+1$
;
$2g+1$
; -
(ii) if f has a pole of order
 $d>1$
at infinity, the genus of D is 2g;
$d>1$
at infinity, the genus of D is 2g; -
(iii) if f has a simple pole at infinity, write
 $f = cx + F$
for a constant
$f = cx + F$
for a constant
 $c\in\mathbb{F}_q^\times$
and a rational function F with no pole at infinity. Then the genus of D is 2g if
$c\in\mathbb{F}_q^\times$
and a rational function F with no pole at infinity. Then the genus of D is 2g if
 $a\ne c$
, and is
$a\ne c$
, and is
 $2g-1$
if
$2g-1$
if
 $a = c$
.
$a = c$
.
Proof. Each finite pole of f, say of order d, gives rise to two finite poles of h, each of order d, and if f has no pole at infinity then neither does h. If f has a total of r poles, none of them at infinity, of orders
![]() $d_1,\ldots, d_r$
, then h has 2r poles, of orders
$d_1,\ldots, d_r$
, then h has 2r poles, of orders
![]() $d_1, d_1, d_2, d_2, \ldots, d_r, d_r$
, and the genus of D is given by
$d_1, d_1, d_2, d_2, \ldots, d_r, d_r$
, and the genus of D is given by
Suppose f has a pole at infinity of order d. We can write
where the
![]() $c_i$
are elements in
$c_i$
are elements in
![]() $\mathbb{F}_q$
with
$\mathbb{F}_q$
with
![]() $c_d\ne0$
and F is a rational function with no pole at infinity. Then the polar decomposition of h at infinity is
$c_d\ne0$
and F is a rational function with no pole at infinity. Then the polar decomposition of h at infinity is
If
![]() $d>1$
we can replace y with
$d>1$
we can replace y with
![]() $y + (\sqrt{c_d/a^d})x^d$
to find that at infinity the curve D looks like
$y + (\sqrt{c_d/a^d})x^d$
to find that at infinity the curve D looks like
The contribution of the pole of h at infinity to the genus of D is d, while the contribution of the pole of f at infinity to the genus of C is
![]() $(d+1)/2$
. Combining this with the contributions of the finite poles, which behave as above, we find that the genus of D is 2g.
$(d+1)/2$
. Combining this with the contributions of the finite poles, which behave as above, we find that the genus of D is 2g.
On the other hand, if
![]() $d=1$
then we have
$d=1$
then we have
and by replacing y with
![]() $y + (\sqrt{c_1/a})x$
we find that at infinity the curve
$y + (\sqrt{c_1/a})x$
we find that at infinity the curve
![]() $D_a$
looks like
$D_a$
looks like
If
![]() $a\ne c_1$
then the coefficient of x is nonzero and the contribution of the pole at infinity to the genus is 1, and we compute as above that the genus of D is 2g. On the other hand, if
$a\ne c_1$
then the coefficient of x is nonzero and the contribution of the pole at infinity to the genus is 1, and we compute as above that the genus of D is 2g. On the other hand, if
![]() $a = c_1$
then the pole at infinity can be removed, and there is no contribution to the genus. In this case we check that the genus of D is
$a = c_1$
then the pole at infinity can be removed, and there is no contribution to the genus. In this case we check that the genus of D is
![]() $2g-1$
.
$2g-1$
.
Lemma 4·11.
Let q be power of 2 and let
![]() $C/\mathbb{F}_q$
be a hyperelliptic curve of genus g with fewer than
$C/\mathbb{F}_q$
be a hyperelliptic curve of genus g with fewer than
![]() $q+1$
rational Weierstrass points. Then there is a hyperelliptic curve D of genus
$q+1$
rational Weierstrass points. Then there is a hyperelliptic curve D of genus
![]() $2g+1$
that is a double cover of C and that has at least as many rational points as does C.
$2g+1$
that is a double cover of C and that has at least as many rational points as does C.
If in addition C has at least two rational Weierstrass points, then D can be chosen to have at least two rational points.
Remark 4·12. If
![]() $C/\mathbb{F}_q$
is a hyperelliptic curve with
$C/\mathbb{F}_q$
is a hyperelliptic curve with
![]() $\#C(\mathbb{F}_q) > q + 1$
then C has fewer than
$\#C(\mathbb{F}_q) > q + 1$
then C has fewer than
![]() $q+1$
rational Weierstrass points.
$q+1$
rational Weierstrass points.
Proof. Let
![]() $\varphi$
be the canonical map from C to
$\varphi$
be the canonical map from C to
![]() $\mathbb{P}^1$
. There is at least one point of
$\mathbb{P}^1$
. There is at least one point of
![]() $\mathbb{P}^1$
that does not ramify in
$\mathbb{P}^1$
that does not ramify in
![]() $\varphi$
, and we can pick one such point and choose a coordinate function x on
$\varphi$
, and we can pick one such point and choose a coordinate function x on
![]() $\mathbb{P}^1$
so that this point lies at
$\mathbb{P}^1$
so that this point lies at
![]() $\infty$
. This means that C has a hyperelliptic model of the form
$\infty$
. This means that C has a hyperelliptic model of the form
![]() $y^2 + y = f$
, where
$y^2 + y = f$
, where
![]() $f\in\mathbb{F}_q(x)$
is a rational function, all of whose poles have odd order, and with no pole at
$f\in\mathbb{F}_q(x)$
is a rational function, all of whose poles have odd order, and with no pole at
![]() $\infty$
.
$\infty$
.
Let n be an element of
![]() $\mathbb{F}_q$
whose absolute trace — that is, its trace to
$\mathbb{F}_q$
whose absolute trace — that is, its trace to
![]() $\mathbb{F}_2$
— is equal to 1. Consider the two hyperelliptic curves
$\mathbb{F}_2$
— is equal to 1. Consider the two hyperelliptic curves
![]() $D\colon y^2 + y = f(x^2 + x)$
and
$D\colon y^2 + y = f(x^2 + x)$
and
![]() $D'\colon y^2 + y = f(x^2 + x + n)$
. By Lemma 4·10, both D and D
′ have genus
$D'\colon y^2 + y = f(x^2 + x + n)$
. By Lemma 4·10, both D and D
′ have genus
![]() $2g+1$
. Also, the obvious double covers
$2g+1$
. Also, the obvious double covers
![]() $D\to C$
and
$D\to C$
and
![]() $D'\to C$
are quadratic twists of one another, and it follows that
$D'\to C$
are quadratic twists of one another, and it follows that
![]() $\#D(\mathbb{F}_q) + \#D'(\mathbb{F}_q) = 2\#C(\mathbb{F}_q)$
. Therefore, one of these two curves has at least as many rational points as does C.
$\#D(\mathbb{F}_q) + \#D'(\mathbb{F}_q) = 2\#C(\mathbb{F}_q)$
. Therefore, one of these two curves has at least as many rational points as does C.
Suppose C has at least two rational Weierstrass points. We can choose our coordinate function x so that one of these points lies over the point
![]() $x=0$
of
$x=0$
of
![]() $\mathbb{P}^1$
, while the other lies over the point
$\mathbb{P}^1$
, while the other lies over the point
![]() $x=n$
of
$x=n$
of
![]() $\mathbb{P}^1$
, where n is an element of
$\mathbb{P}^1$
, where n is an element of
![]() $\mathbb{F}_q$
of absolute trace 1. The Weierstrass point lying over
$\mathbb{F}_q$
of absolute trace 1. The Weierstrass point lying over
![]() $x=0$
splits into two rational Weierstrass points of D, and the Weierstrass point lying over
$x=0$
splits into two rational Weierstrass points of D, and the Weierstrass point lying over
![]() $x=n$
splits into two rational Weierstrass points of D
′. Therefore, no matter which of the two curves has at least as many rational points as C, it has at least two rational Weierstrass points.
$x=n$
splits into two rational Weierstrass points of D
′. Therefore, no matter which of the two curves has at least as many rational points as C, it has at least two rational Weierstrass points.
Lemma 4·13.
Let
![]() $q>2$
be a power of 2 and let
$q>2$
be a power of 2 and let
![]() $C/\mathbb{F}_q$
be a hyperelliptic curve of genus g that has at least two rational Weierstrass points and with
$C/\mathbb{F}_q$
be a hyperelliptic curve of genus g that has at least two rational Weierstrass points and with
![]() $\#C(\mathbb{F}_q) > q$
. Then there is a hyperelliptic curve
$\#C(\mathbb{F}_q) > q$
. Then there is a hyperelliptic curve
![]() $D/\mathbb{F}_q$
of genus 2g that is a double cover of C, that has at least two rational Weierstrass points, and that satisfies
$D/\mathbb{F}_q$
of genus 2g that is a double cover of C, that has at least two rational Weierstrass points, and that satisfies
 \begin{alignat*}{2}\#D(\mathbb{F}_q) &\ge \#C(\mathbb{F}_q)&\qquad&\text{if $\#C(\mathbb{F}_q) < 2q$}{;}\\[5pt] \#D(\mathbb{F}_q) &= 2q-1 & &\text{if $\#C(\mathbb{F}_q) = 2q$.}\end{alignat*}
\begin{alignat*}{2}\#D(\mathbb{F}_q) &\ge \#C(\mathbb{F}_q)&\qquad&\text{if $\#C(\mathbb{F}_q) < 2q$}{;}\\[5pt] \#D(\mathbb{F}_q) &= 2q-1 & &\text{if $\#C(\mathbb{F}_q) = 2q$.}\end{alignat*}
Proof. Let
![]() $\varphi\colon C\to\mathbb{P}^1$
be the canonical double cover. Suppose C has at least three rational Weierstrass points. We can choose a coordinate function x on
$\varphi\colon C\to\mathbb{P}^1$
be the canonical double cover. Suppose C has at least three rational Weierstrass points. We can choose a coordinate function x on
![]() $\mathbb{P}^1$
so that these three points lie over 0, n, and
$\mathbb{P}^1$
so that these three points lie over 0, n, and
![]() $\infty$
, where n is an element of
$\infty$
, where n is an element of
![]() $\mathbb{F}_q$
of absolute trace 1. If f has a simple pole at infinity and if the coefficient
$\mathbb{F}_q$
of absolute trace 1. If f has a simple pole at infinity and if the coefficient
![]() $c_1$
of x in the polar expansion (4·1) is equal to 1, we can choose another element n
′ of
$c_1$
of x in the polar expansion (4·1) is equal to 1, we can choose another element n
′ of
![]() $\mathbb{F}_q$
of absolute trace 1 and then scale x by a factor of
$\mathbb{F}_q$
of absolute trace 1 and then scale x by a factor of
![]() $n'/n$
; this has the effect of replacing n with n
′ and of modifying the coefficient
$n'/n$
; this has the effect of replacing n with n
′ and of modifying the coefficient
![]() $c_1$
so that it is no longer equal to 1. Thus, we may assume that
$c_1$
so that it is no longer equal to 1. Thus, we may assume that
![]() $c_1\ne 1$
.
$c_1\ne 1$
.
Consider the two curves
![]() $D\colon y^2 + y = f(x^2 + x)$
and
$D\colon y^2 + y = f(x^2 + x)$
and
![]() $D'\colon y^2 + y = f(x^2 + x + n)$
. We see from Lemma 4·10 that both D and D
′ have genus 2g, and one of them has at least as many rational points as does C. Furthermore, the Weierstrass point of C that lies above
$D'\colon y^2 + y = f(x^2 + x + n)$
. We see from Lemma 4·10 that both D and D
′ have genus 2g, and one of them has at least as many rational points as does C. Furthermore, the Weierstrass point of C that lies above
![]() $x=0$
splits into two rational Weierstrass points on D, while the Weierstrass point of C lying above (n,0) splits into two rational Weierstrass points on D
′. Thus, at least one of D and D
′ will satisfy the conclusion of the lemma.
$x=0$
splits into two rational Weierstrass points on D, while the Weierstrass point of C lying above (n,0) splits into two rational Weierstrass points on D
′. Thus, at least one of D and D
′ will satisfy the conclusion of the lemma.
We can now turn to the case where C has exactly two rational Weierstrass points. This time, we can choose a coordinate function x on
![]() $\mathbb{P}^1$
so that C has a hyperelliptic model of the form
$\mathbb{P}^1$
so that C has a hyperelliptic model of the form
![]() $y^2 + y = f$
, where
$y^2 + y = f$
, where
![]() $f\in \mathbb{F}_q(x)$
is a rational function that has odd-order poles at 0 and
$f\in \mathbb{F}_q(x)$
is a rational function that has odd-order poles at 0 and
![]() $\infty$
and no other rational poles. If
$\infty$
and no other rational poles. If
![]() $\#C(\mathbb{F}_q) < 2q$
, then there must be a rational point of
$\#C(\mathbb{F}_q) < 2q$
, then there must be a rational point of
![]() $\mathbb{P}^1$
that does not have a rational point of C lying over it; in this case, we scale x so that this point becomes the point
$\mathbb{P}^1$
that does not have a rational point of C lying over it; in this case, we scale x so that this point becomes the point
![]() $x=1$
of
$x=1$
of
![]() $\mathbb{P}^1$
. In particular, this means that f(1) has absolute trace 1. On the other hand, if
$\mathbb{P}^1$
. In particular, this means that f(1) has absolute trace 1. On the other hand, if
![]() $\#C(\mathbb{F}_q) = 2q$
, then every point of
$\#C(\mathbb{F}_q) = 2q$
, then every point of
![]() $\mathbb{P}^1(\mathbb{F}_q)$
other than 0 and
$\mathbb{P}^1(\mathbb{F}_q)$
other than 0 and
![]() $\infty$
splits into two rational points of C, so f(a) has absolute trace 0 for every
$\infty$
splits into two rational points of C, so f(a) has absolute trace 0 for every
![]() $a\in\mathbb{F}_q^\times.$
$a\in\mathbb{F}_q^\times.$
Let n be an element of
![]() $\mathbb{F}_q$
whose absolute trace is 1. For every
$\mathbb{F}_q$
whose absolute trace is 1. For every
![]() $a\in\mathbb{F}_q$
, set
$a\in\mathbb{F}_q$
, set
![]() $h_a\;:\!=\; f((x^2+x)/(a^2+a+n))$
and let
$h_a\;:\!=\; f((x^2+x)/(a^2+a+n))$
and let
![]() $D_a$
be the curve
$D_a$
be the curve
![]() $y^2 + y = h_a$
. If the polynomial
$y^2 + y = h_a$
. If the polynomial
![]() $x^2 + x + n + c_1$
(with
$x^2 + x + n + c_1$
(with
![]() $c_1$
defined in (4·1)) has roots in
$c_1$
defined in (4·1)) has roots in
![]() $\mathbb{F}_q$
, we let
$\mathbb{F}_q$
, we let
![]() $s_0$
and
$s_0$
and
![]() $s_1$
be those roots; otherwise, we take
$s_1$
be those roots; otherwise, we take
![]() $s_1 = 0$
and
$s_1 = 0$
and
![]() $s_2 = 1$
. We see from Lemma 4·10 that
$s_2 = 1$
. We see from Lemma 4·10 that
![]() $D_a$
has genus 2g for all
$D_a$
has genus 2g for all
![]() $a\in\mathbb{F}_q$
different from
$a\in\mathbb{F}_q$
different from
![]() $s_1$
and
$s_1$
and
![]() $s_2$
.
$s_2$
.
Let us compute the number of rational points on
![]() $D_a$
. Let
$D_a$
. Let
![]() $\chi\colon\mathbb{P}^1(\mathbb{F}_q)\to \{-1,0,1\}$
be the function that takes
$\chi\colon\mathbb{P}^1(\mathbb{F}_q)\to \{-1,0,1\}$
be the function that takes
![]() $\infty$
to 0 and that takes an element
$\infty$
to 0 and that takes an element
![]() $z\in\mathbb{F}_q$
to 1 or
$z\in\mathbb{F}_q$
to 1 or
![]() $-1$
depending on whether the absolute trace of z is 0 or 1. We see, for example, that
$-1$
depending on whether the absolute trace of z is 0 or 1. We see, for example, that
just as we had in odd characteristic. Let
![]() $n_a$
be the number of rational points on
$n_a$
be the number of rational points on
![]() $D_a$
at infinity, so that
$D_a$
at infinity, so that
![]() $n_a = 1$
if
$n_a = 1$
if
![]() $D_a$
has a Weierstrass point at infinity and
$D_a$
has a Weierstrass point at infinity and
![]() $n_a$
is either 0 or 2 otherwise. Arguing as in the odd-characteristic case, we find that
$n_a$
is either 0 or 2 otherwise. Arguing as in the odd-characteristic case, we find that
 \begin{align*}\#D_a(\mathbb{F}_q)&= n_a + \sum_{z\in\mathbb{F}_q}(1 + \chi((a^2+a+n)z))(1 + \chi(f(z)))\\[5pt] &= n_a - 1 + \#C(\mathbb{F}_q) + \sum_{z\in\mathbb{F}_q}\chi((a^2+a+n)z) + \sum_{z\in\mathbb{F}_q} \chi((a^2+a+n)z)\chi(f(z))\\[5pt] &= n_a - 1 + \#C(\mathbb{F}_q) + \sum_{z\in\mathbb{F}_q} \chi((a^2+a+n)z)\chi(f(z))\,.\end{align*}
\begin{align*}\#D_a(\mathbb{F}_q)&= n_a + \sum_{z\in\mathbb{F}_q}(1 + \chi((a^2+a+n)z))(1 + \chi(f(z)))\\[5pt] &= n_a - 1 + \#C(\mathbb{F}_q) + \sum_{z\in\mathbb{F}_q}\chi((a^2+a+n)z) + \sum_{z\in\mathbb{F}_q} \chi((a^2+a+n)z)\chi(f(z))\\[5pt] &= n_a - 1 + \#C(\mathbb{F}_q) + \sum_{z\in\mathbb{F}_q} \chi((a^2+a+n)z)\chi(f(z))\,.\end{align*}
Define
so that
Suppose
![]() $\#C(\mathbb{F}_q) = 2q$
, so that
$\#C(\mathbb{F}_q) = 2q$
, so that
![]() $\chi(f(z)) = 1$
for all
$\chi(f(z)) = 1$
for all
![]() $z\in\mathbb{F}_q^\times$
. Then for every
$z\in\mathbb{F}_q^\times$
. Then for every
![]() $a\in\mathbb{F}_q\setminus\{s_0,s_1\}$
we have
$a\in\mathbb{F}_q\setminus\{s_0,s_1\}$
we have
and for such a we also know that
![]() $n_a=1$
. Thus, for every such a the curve
$n_a=1$
. Thus, for every such a the curve
![]() $D_a$
has
$D_a$
has
![]() $2q-1$
points, and so satisfies the conditions listed in the lemma.
$2q-1$
points, and so satisfies the conditions listed in the lemma.
We are left with the case where
![]() $\#C(\mathbb{F}_q)<2q$
. We will show that in this case there is an
$\#C(\mathbb{F}_q)<2q$
. We will show that in this case there is an
![]() $a\in\mathbb{F}_q$
, not equal to
$a\in\mathbb{F}_q$
, not equal to
![]() $s_1$
or
$s_1$
or
![]() $s_2$
, such that
$s_2$
, such that
![]() $N_a\ge 0$
. Recall that in this case, we normalised f so that
$N_a\ge 0$
. Recall that in this case, we normalised f so that
![]() $\chi(f(1)) = -1$
.
$\chi(f(1)) = -1$
.
We compute:
 \begin{align*}\sum_{a\in\mathbb{F}_q} N_{a}&= \sum_{a\in\mathbb{F}_q} \sum_{z\in\mathbb{F}_q} \chi((a^2 + a + n)z)\chi(f(z))\\[5pt] &= \sum_{z\in\mathbb{F}_q} \chi(f(z)) \sum_{a\in\mathbb{F}_q} \chi((a^2+a+n)z)\,.\end{align*}
\begin{align*}\sum_{a\in\mathbb{F}_q} N_{a}&= \sum_{a\in\mathbb{F}_q} \sum_{z\in\mathbb{F}_q} \chi((a^2 + a + n)z)\chi(f(z))\\[5pt] &= \sum_{z\in\mathbb{F}_q} \chi(f(z)) \sum_{a\in\mathbb{F}_q} \chi((a^2+a+n)z)\,.\end{align*}
When
![]() $z = 0$
, the interior sum is equal to q. When
$z = 0$
, the interior sum is equal to q. When
![]() $z = 1$
, the interior sum is equal to
$z = 1$
, the interior sum is equal to
![]() $-q$
. When
$-q$
. When
![]() $z\in\mathbb{F}_q\setminus\mathbb{F}_2$
, we calculate the interior sum as follows. Let
$z\in\mathbb{F}_q\setminus\mathbb{F}_2$
, we calculate the interior sum as follows. Let
![]() $X_z$
be the genus-0 curve
$X_z$
be the genus-0 curve
![]() $y^2 + y = z(x^2 + x + n)$
. Then
$y^2 + y = z(x^2 + x + n)$
. Then
so
Therefore,
Now, from (4·2) we find that
![]() $N_a = (\#D_a(\mathbb{F}_q)-n_a) - (\#C(\mathbb{F}_q)-1)$
, so that
$N_a = (\#D_a(\mathbb{F}_q)-n_a) - (\#C(\mathbb{F}_q)-1)$
, so that
![]() $N_a$
is the difference between the number of rational points of
$N_a$
is the difference between the number of rational points of
![]() $D_a$
not lying over
$D_a$
not lying over
![]() $\infty$
and the number of rational points of C not lying over
$\infty$
and the number of rational points of C not lying over
![]() $\infty$
. Since
$\infty$
. Since
![]() $D_a$
has two rational Weierstrass points not lying over
$D_a$
has two rational Weierstrass points not lying over
![]() $\infty$
we have
$\infty$
we have
![]() $\#D_a(\mathbb{F}_q)-n_a\le 2q-2$
, so
$\#D_a(\mathbb{F}_q)-n_a\le 2q-2$
, so
![]() $N_a\le 2q-1-\#C(\mathbb{F}_q)$
. Suppose, to obtain a contradiction, that for every
$N_a\le 2q-1-\#C(\mathbb{F}_q)$
. Suppose, to obtain a contradiction, that for every
![]() $a\in\mathbb{F}_q$
other than
$a\in\mathbb{F}_q$
other than
![]() $s_1$
and
$s_1$
and
![]() $s_2$
we had
$s_2$
we had
![]() $\#D_a(\mathbb{F}_q) < \#C(\mathbb{F}_q)$
, so that
$\#D_a(\mathbb{F}_q) < \#C(\mathbb{F}_q)$
, so that
![]() $N_a\le -1$
. Then we would have
$N_a\le -1$
. Then we would have
so that
![]() $\#C(\mathbb{F}_q)\le q$
. This contradicts the hypothesis of the lemma. Therefore, there is at least one value of a for which
$\#C(\mathbb{F}_q)\le q$
. This contradicts the hypothesis of the lemma. Therefore, there is at least one value of a for which
![]() $D_a$
has genus 2g and
$D_a$
has genus 2g and
![]() $\#D_a(\mathbb{F}_q)\ge\#C(\mathbb{F}_q)$
. We have already seen that every such
$\#D_a(\mathbb{F}_q)\ge\#C(\mathbb{F}_q)$
. We have already seen that every such
![]() $D_a$
has three rational Weierstrass points, so we are done.
$D_a$
has three rational Weierstrass points, so we are done.
Lemmas 4·11 and 4·13 give us the machinery with which to build an induction as in the previous subsection, and once again we are left with the task of producing curves of genus 2 and 3 with many points to use as base cases. Such curves are provided by the following lemma.
Lemma 4·14.
Let q be a power of 2 with
![]() $q>8$
. Then for
$q>8$
. Then for
![]() $g=2$
and
$g=2$
and
![]() $g=3$
there is a hyperelliptic curve
$g=3$
there is a hyperelliptic curve
![]() $C/\mathbb{F}_q$
of genus g with at least two rational Weierstrass points and with
$C/\mathbb{F}_q$
of genus g with at least two rational Weierstrass points and with
![]() $\#C(\mathbb{F}_q) > 1 + q + 4\sqrt{q} - 12$
.
$\#C(\mathbb{F}_q) > 1 + q + 4\sqrt{q} - 12$
.
Proof. We observe that an ordinary elliptic curve over
![]() $\mathbb{F}_q$
can be written in the form
$\mathbb{F}_q$
can be written in the form
![]() $y^2 + y = x + a/x$
if and only if it has a rational point of order 4, one such point being
$y^2 + y = x + a/x$
if and only if it has a rational point of order 4, one such point being
![]() $(\sqrt{a},0)$
. Furthermore, such a curve has a rational point of order 8 if and only if a has absolute trace 0; in this case, if we write
$(\sqrt{a},0)$
. Furthermore, such a curve has a rational point of order 8 if and only if a has absolute trace 0; in this case, if we write
![]() $a = b^2 + b$
, then an 8-torsion point is given by
$a = b^2 + b$
, then an 8-torsion point is given by
![]() $((a^4 + a^3)^{1/4}, b^{1/4})$
.
$((a^4 + a^3)^{1/4}, b^{1/4})$
.
Let
![]() $t_0$
and
$t_0$
and
![]() $t_4$
be the largest integers less than or equal to
$t_4$
be the largest integers less than or equal to
![]() $2\sqrt{q}$
such that
$2\sqrt{q}$
such that
![]() $1 + q + t_0\equiv 0\bmod 8$
and
$1 + q + t_0\equiv 0\bmod 8$
and
![]() $1 + q + t_4\equiv 4\bmod 8$
, so that
$1 + q + t_4\equiv 4\bmod 8$
, so that
![]() $t_i>2\sqrt{q} - 8$
for both values of i and
$t_i>2\sqrt{q} - 8$
for both values of i and
![]() $t_i>2\sqrt{q} - 4$
for one value of i. For
$t_i>2\sqrt{q} - 4$
for one value of i. For
![]() $i=0$
and
$i=0$
and
![]() $i=4$
, let
$i=4$
, let
![]() $E_i$
be an ordinary elliptic curve over
$E_i$
be an ordinary elliptic curve over
![]() $\mathbb{F}_q$
with trace
$\mathbb{F}_q$
with trace
![]() $t_i$
. Then we can write the
$t_i$
. Then we can write the
![]() $E_i$
in the form
$E_i$
in the form
![]() $y^2 + y = x + a_i/x$
, where
$y^2 + y = x + a_i/x$
, where
![]() $a_0$
has absolute trace 0 and
$a_0$
has absolute trace 0 and
![]() $a_4$
has absolute trace 1.
$a_4$
has absolute trace 1.
Let C be the hyperelliptic curve
Clearly C has three rational Weierstrass points. Also, if we set
![]() $z = y + \sqrt{a_i/(a_0+a_4)} x$
, then
$z = y + \sqrt{a_i/(a_0+a_4)} x$
, then
and the quotient of this curve by the involution that sends (x,z) to
![]() $(x+1,z)$
is clearly
$(x+1,z)$
is clearly
which we check is isomorphic to
![]() $E_i$
. Therefore
$E_i$
. Therefore
![]() $\textrm{Jac} C$
is isogenous to
$\textrm{Jac} C$
is isogenous to
![]() $E_0\times E_4$
, so
$E_0\times E_4$
, so
![]() $\#C(\mathbb{F}_q) = 1 + q + t_0 + t_4 > 1 + q + 4\sqrt{q} - 12.$
$\#C(\mathbb{F}_q) = 1 + q + t_0 + t_4 > 1 + q + 4\sqrt{q} - 12.$
Now let D be the double cover of C obtained by adjoining a root of
to the function field of C. Combining equations (4·3) and (4·4) and writing
![]() $v = y + u$
, we find that D can be written in the form
$v = y + u$
, we find that D can be written in the form
Because the absolute trace of
![]() $a_0 + a_4$
is 1, the quadratic twist
$a_0 + a_4$
is 1, the quadratic twist
![]() $D'\to C$
of the double cover
$D'\to C$
of the double cover
![]() $D\to C$
can be given by
$D\to C$
can be given by
One of the two curves D and D
′ will have at least as many points as C, and D and D
′ each have exactly two rational Weierstrass points: On both curves, the points with
![]() $u=0$
and
$u=0$
and
![]() $u=1$
are Weierstrass points. Thus, one of D and D
′ will be a hyperelliptic curve of genus 3 with the desired properties.
$u=1$
are Weierstrass points. Thus, one of D and D
′ will be a hyperelliptic curve of genus 3 with the desired properties.
Proof of Theorem 4·1 (ii). For
![]() $q=2$
, 4 and 8, we need to show that there are hyperelliptic curves of every genus
$q=2$
, 4 and 8, we need to show that there are hyperelliptic curves of every genus
![]() $g>1$
with at least 4, 9 and 16 points, respectively. For
$g>1$
with at least 4, 9 and 16 points, respectively. For
![]() $q=2$
and
$q=2$
and
![]() $q = 4$
this follows from Lemma 4·15 below. For
$q = 4$
this follows from Lemma 4·15 below. For
![]() $q=8$
, Lemma 4·15 gives us the desired hyperelliptic curve when
$q=8$
, Lemma 4·15 gives us the desired hyperelliptic curve when
![]() $g\ge 4$
, so we are left to find examples of genus 2 and genus 3. These are provided by the genus-2 curve
$g\ge 4$
, so we are left to find examples of genus 2 and genus 3. These are provided by the genus-2 curve
![]() $y^2 + y = x^5 + x^3$
and the genus-3 curve
$y^2 + y = x^5 + x^3$
and the genus-3 curve
![]() $y^2 + y = rx^7$
, where r satisfies
$y^2 + y = rx^7$
, where r satisfies
![]() $r^3 + r + 1 = 0$
; both of these curves have 17 rational points.
$r^3 + r + 1 = 0$
; both of these curves have 17 rational points.
Now assume that
![]() $q>8$
. We prove the result by induction on g. The statement is true for
$q>8$
. We prove the result by induction on g. The statement is true for
![]() $g=2$
and
$g=2$
and
![]() $g=3$
by Lemma 4·14. Now suppose Theorem 4·1(ii) holds for all g less than some integer
$g=3$
by Lemma 4·14. Now suppose Theorem 4·1(ii) holds for all g less than some integer
![]() $G>3$
. We will show it also holds when
$G>3$
. We will show it also holds when
![]() $g = G$
.
$g = G$
.
Set
![]() $h = \lfloor G/2\rfloor$
. Then
$h = \lfloor G/2\rfloor$
. Then
![]() $h>1$
, and we may apply Theorem 4·1(ii) to show that for every q, there is a hyperelliptic curve
$h>1$
, and we may apply Theorem 4·1(ii) to show that for every q, there is a hyperelliptic curve
![]() $C/\mathbb{F}_q$
of genus h with at least two rational Weierstrass points and with
$C/\mathbb{F}_q$
of genus h with at least two rational Weierstrass points and with
![]() $\#C(\mathbb{F}_q) > 1 + q + 4\sqrt{q} - 12$
.
$\#C(\mathbb{F}_q) > 1 + q + 4\sqrt{q} - 12$
.
If G is odd, we apply Lemma 4·11 to the curve C and find that there is a hyperelliptic curve D of genus
![]() $2h+1 = G$
with at least two rational Weierstrass points and with
$2h+1 = G$
with at least two rational Weierstrass points and with
![]() $\#D(\mathbb{F}_q)\ge \#C(\mathbb{F}_q)$
.
$\#D(\mathbb{F}_q)\ge \#C(\mathbb{F}_q)$
.
If G is even, we apply Lemma 4·13 to the curve C and find that there is a hyperelliptic curve D of genus
![]() $2h = G$
with at least two rational Weierstrass points and with
$2h = G$
with at least two rational Weierstrass points and with
![]() $\#D(\mathbb{F}_q)\ge \#C(\mathbb{F}_q)$
or with
$\#D(\mathbb{F}_q)\ge \#C(\mathbb{F}_q)$
or with
![]() $\#D(\mathbb{F}_q) = 2q-1$
.
$\#D(\mathbb{F}_q) = 2q-1$
.
Lemma 4·15.
Let
![]() $q>1$
be a power of 2 and let g be an integer with
$q>1$
be a power of 2 and let g be an integer with
![]() $g\ge q/2$
. Then there is a hyperelliptic curve of genus g over
$g\ge q/2$
. Then there is a hyperelliptic curve of genus g over
![]() $\mathbb{F}_q$
having
$\mathbb{F}_q$
having
![]() $2q+1$
rational points.
$2q+1$
rational points.
Proof. Consider the function
![]() $\mathbb{F}_q\to\mathbb{F}_q$
that sends a to
$\mathbb{F}_q\to\mathbb{F}_q$
that sends a to
![]() $a^{2g+1}$
. By Lagrange interpolation, there is a polynomial
$a^{2g+1}$
. By Lagrange interpolation, there is a polynomial
![]() $f\in\mathbb{F}_q[x]$
of degree at most
$f\in\mathbb{F}_q[x]$
of degree at most
![]() $q-1$
that agrees with this function. Therefore, the polynomial
$q-1$
that agrees with this function. Therefore, the polynomial
![]() $x^{2g+1} + f$
has degree
$x^{2g+1} + f$
has degree
![]() $2g+1$
and evaluates to 0 for every
$2g+1$
and evaluates to 0 for every
![]() $x\in\mathbb{F}_q$
. Therefore the curve
$x\in\mathbb{F}_q$
. Therefore the curve
![]() $y^2 + y = x^{2g+1} + f$
has
$y^2 + y = x^{2g+1} + f$
has
![]() $2q+1$
rational points and has genus g.
$2q+1$
rational points and has genus g.
4·3. Remarks on constructing examples
We mentioned earlier that our arguments in this section suggest an algorithm for constructing the curves whose existence is asserted by Theorem 4·1. In particular, Lemmas 4·8, 4·9 and 4·14 provide explicit ways of finding the base curves of genus 2 and 3 with which to start the construction; these lemmas require that we find an elliptic curve over
![]() $\mathbb{F}_q$
with a certain specific trace and with all of its 2-torsion points rational. In general it is a difficult problem to find an elliptic curve over a given finite field with a given number of points, and the best general algorithm for doing so is essentially to pick elliptic curves at random until one finds one with the desired order. In our case, the discriminant of the endomorphism ring of the curves we want is smaller than average — it’s
$\mathbb{F}_q$
with a certain specific trace and with all of its 2-torsion points rational. In general it is a difficult problem to find an elliptic curve over a given finite field with a given number of points, and the best general algorithm for doing so is essentially to pick elliptic curves at random until one finds one with the desired order. In our case, the discriminant of the endomorphism ring of the curves we want is smaller than average — it’s
![]() $O(\sqrt{q})$
instead of O(q) — so we might choose to use the Hilbert class polynomial method [
Reference SutherlandSut11
] instead.
$O(\sqrt{q})$
instead of O(q) — so we might choose to use the Hilbert class polynomial method [
Reference SutherlandSut11
] instead.
Once we have a starting curve, we need to recursively construct curves in the tower leading to the desired genus. Lemmas 4·3 and 4·11 tell us how to quickly produce a curve of genus
![]() $2g+1$
from a curve of genus g, with the new curve having at least as many points as the old; the work required is simply that of counting points on a single hyperelliptic curve of genus
$2g+1$
from a curve of genus g, with the new curve having at least as many points as the old; the work required is simply that of counting points on a single hyperelliptic curve of genus
![]() $2g+1$
. It is more difficult to produce a curve of genus 2g from a curve of genus g, with the new curve having at least as many points as the old. Lemmas 4·5 and 4·13 tell us that there is at least one curve in an explicit one-parameter family with the desired properties, but in the worst case we might have to count points on essentially all curves in the family before finding one that works. Heuristically, though, we expect to find a good curve after only a few tries.
$2g+1$
. It is more difficult to produce a curve of genus 2g from a curve of genus g, with the new curve having at least as many points as the old. Lemmas 4·5 and 4·13 tell us that there is at least one curve in an explicit one-parameter family with the desired properties, but in the worst case we might have to count points on essentially all curves in the family before finding one that works. Heuristically, though, we expect to find a good curve after only a few tries.
In the worst case, then, we might need to count points on as many as
![]() $O(q\log g)$
hyperelliptic curves over
$O(q\log g)$
hyperelliptic curves over
![]() $\mathbb{F}_q$
in order to find a curve of genus g over
$\mathbb{F}_q$
in order to find a curve of genus g over
![]() $\mathbb{F}_q$
with close to
$\mathbb{F}_q$
with close to
![]() $q + 1 + 4\sqrt{q}$
points. In practice, we find that many fewer steps are required, and we expect the algorithm sketched above to require counting points on
$q + 1 + 4\sqrt{q}$
points. In practice, we find that many fewer steps are required, and we expect the algorithm sketched above to require counting points on
![]() $O(\log g)$
hyperelliptic curves, once we have found the base curve of genus 2 or 3.
$O(\log g)$
hyperelliptic curves, once we have found the base curve of genus 2 or 3.
We might compare this heuristic complexity to that of the naïve method of picking hyperelliptic curves of genus g over
![]() $\mathbb{F}_q$
at random until we find one with close to
$\mathbb{F}_q$
at random until we find one with close to
![]() $q + 1 \pm 4\sqrt{q}$
points. Essentially, the naïve method requires waiting for a four-sigma event to occur, so we might expect to try about 15,000 curves on average before finding one with more than
$q + 1 \pm 4\sqrt{q}$
points. Essentially, the naïve method requires waiting for a four-sigma event to occur, so we might expect to try about 15,000 curves on average before finding one with more than
![]() $q + 1 + 4\sqrt{q}$
points.
$q + 1 + 4\sqrt{q}$
points.
Acknowledgements
The idea of using sums of powers of traces of Frobenius over the collection of all genus-g hyperelliptic curves, which we use in Section 3, was suggested to us in a personal communication by J-P. Serre. We want to thank him for his generous input, which initiated this whole project. We also thank Markus Kirschmer for his help with the mass formulae in Remark 2·5. Finally, we thank Jeff Achter, Anna Cadoret, Adrian Diaconu and Rachel Pries for their helpful comments on the first version of this paper. The last author contributed to this paper during his time at the laboratory Jean Alexandre Dieudonné of the University Côte d’Azur in Nice.