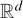Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Persi Diaconis
Xuancheng Shao
and
Kannan Soundararajan
2014.
Carries, Group Theory, and Additive Combinatorics.
The American Mathematical Monthly,
Vol. 121,
Issue. 8,
p.
674.
Manners, Frederick R. W. M.
2016.
Finding a Low-dimensional Piece of a Set of Integers.
International Mathematics Research Notices,
p.
rnw153.