Hostname: page-component-7479d7b7d-qs9v7 Total loading time: 0 Render date: 2024-07-11T18:24:08.893Z Has data issue: false hasContentIssue false
  • English
  • Français

A homotopy decomposition for the classifying space of virtually torsion-free groups and applications

Published online by Cambridge University Press:  24 October 2008

Chun-Nip Lee
Chun-Nip Lee
Affiliation:
Department of Mathematics, Northwestern University, Evanston, IL 60208, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let Γ be a discrete group. Γ is said to have finite virtual cohomological dimension (vcd) if there exists a finite index torsion-free subgroup Γ' of Γ such that Γ' has finite cohomological dimension over 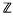. Examples of such groups include the fundamental group of a finite graph of finite groups, arithmetic groups, mapping class groups and outer automorphism groups of free groups. One of the fundamental problems in topology is to understand the cohomology of these finite vcd-groups.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 4 , November 1996 , pp. 663 - 686
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adem, A.. On the exponent of cohomology of discrete groups. Bull. London Math. Soc. 21 (1989), 585–590.CrossRefGoogle Scholar
[2]Adem, A.. Torsion in equivariant cohomology. Comment. Math. Helvetici 64 (1989), 401–411.CrossRefGoogle Scholar
[3]Adem, A.. On the K-theory of the classifying space of a discrete group. Math. Ann. 292 (1992), 319–327.CrossRefGoogle Scholar
[4]Adem, A.. Representations and K-theory of discrete groups. Bull. Amer. Math. Soc. 28 (1993), 95–98.CrossRefGoogle Scholar
[5]Adem, A., Cohen, R. L. and Dwyer, W. G.. Generalized Tate homology, homotopy fixed points and the transfer. Contemporary Mathematics 96 (1989), 1–13.CrossRefGoogle Scholar
[6]Atiyah, M. F. and Segal, G. B.. Equivariant K-theory and completion. J. Diff. Geom. 3 (1969), 1–18.Google Scholar
[7]Bousfield, A. K. and Kan, D. M.. Homotopy limits, completions and localizations. Lect. Notes in Math. 304 (Springer, 1972).Google Scholar
[8]Beedon, G. E.. Introduction to compact transformation groups (Academic Press, 1972).Google Scholar
[9]Brown, K.. Cohomology of groups. Graduate Texts in Math., vol. 87 (Springer, 1982).CrossRefGoogle Scholar
[10]Carlsson, G.. Equivariant stable homotopy and Segal's Burnside ring conjecture. Annals of Math. 120 (1984), 189–224.CrossRefGoogle Scholar
[11]Cartan, H. and Eilenberg, S.. Homological algebra (Princeton University Press, 1965).Google Scholar
[12]Greenlees, J. P. C.. Representing Tate cohomology of G-spaces. Proc. Edinburgh Math. Soc. 30 (1987), 435–443.CrossRefGoogle Scholar
[13]Jackowski, S. and McClure, J.. Homotopy decomposition of classifying spaces via elementary abelian subgroups. Topology 31 (1992), 113–132.CrossRefGoogle Scholar
[14]Jackowski, S., McClure, J. and Oliver, R.. Homotopy classification of self-maps of BG via G-actions: I. Annals of Mathematics 135 (1992), 183–226; II, 227–270.CrossRefGoogle Scholar
[15]Lewis, G., May, J. P. and Steinberger, M.. Equivariant stable homotopy theory, Lect. Notes in Math. 1213 (Springer-Verlag, 1986).Google Scholar
[16]Miyazaki, H.The paracompactness of CW-complexes. Tohoku Math. J. 4 (1953), 309–315.Google Scholar
[17]Oliver, R.. A proof of the Conner conjecture. Ann. of Math. 103 (1976), 637–644.CrossRefGoogle Scholar
[18]Oliver, R.. Higher limits via Steinberg representations. Comm. in Algebra 22 (1994), 1381–1393.CrossRefGoogle Scholar
[19]Quillen, D.. The spectrum of an equivariant cohomology ring: I. Ann. Math. 94 (1971), 549–572; II, 573–602.CrossRefGoogle Scholar
[20]Spanier, E.. Algebraic topology(Springer-Verlag, 1966).Google Scholar
[21]Xia, Y.. The p-torsion of the Farrell–Tate cohomology of the mapping class group in Topology 90', Proceedings of the Research Semester in Low Dimensional Topology at Ohio State University (de Gruyter, 1992), pp. 391–398.CrossRefGoogle Scholar