Hostname: page-component-77c89778f8-gvh9x Total loading time: 0 Render date: 2024-07-16T19:37:40.962Z Has data issue: false hasContentIssue false
  • English
  • Français

A heat trace anomaly on polygons

Published online by Cambridge University Press:  19 June 2015

RAFE MAZZEO  and
JULIE ROWLETT
RAFE MAZZEO
Affiliation:
Department of Mathematics, Stanford University, Building 380, Stanford, CA 94305, U.S.A. e-mail: mazzeo@math.standord.edu
JULIE ROWLETT
Affiliation:
Mathematical Sciences, Chalmers University of Technology and the University of Gothenburg, SE-412 96 Göteborg, Sweden e-mail: julie.rowlett@chalmers.se
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Ω0 be a polygon in 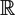$\mathbb{R}$2, or more generally a compact surface with piecewise smooth boundary and corners. Suppose that Ωε is a family of surfaces with 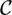${\mathcal C}$∞ boundary which converges to Ω0 smoothly away from the corners, and in a precise way at the vertices to be described in the paper. Fedosov [6], Kac [8] and McKean–Singer [13] recognised that certain heat trace coefficients, in particular the coefficient of t0, are not continuous as ε ↘ 0. We describe this anomaly using renormalized heat invariants of an auxiliary smooth domain Z which models the corner formation. The result applies to both Dirichlet and Neumann boundary conditions. We also include a discussion of what one might expect in higher dimensions.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 159 , Issue 2 , September 2015 , pp. 303 - 319
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] van dan Berg, M. and Srisatkunarajah, S. Heat equation for a region in $\mathbb{R}$ 2 with a polygonal boundary. J. London Math. Soc. 2 no. 37 (1988), 119–127.Google Scholar
[2] Cheeger, J. Spectral geometry of singular Riemannian spaces. J. Differential Geom. 18 (1984), 575–657.Google Scholar
[3] Dauge, M., Tordeux, S. and Vial, G. Self-similar perturbations near a corner: matching versus multiscale expansions for a model problem. Around the research of Vladimir Maz'ya. II, Int. Math. Ser. (N. Y.) 12 (Springer, New York, 2010), 95–134.Google Scholar
[4] Davies, E.B. Heat kernels and spectral theory. Cambridge Tracts in Math. 92 (Cambridge University Press, 1989).Google Scholar
[5] Ding, Y. Heat kernels and Green's functions on limit spaces, Comm. Anal. Geom., 10 no. 3 (2002), 475–514.Google Scholar
[6] Fedosov, B. Asymptotic formulas for eigenvalues of the Laplacian in a polyhedron. Doklady Akad. Nauk SSSR 157 (1964), 536–538.Google Scholar
[7] Guillarmou, C. and Hassell, A. Resolvent at low energy and Riesz transform for Schrödinger operators on asymptotically conical manifolds, I. Math. Ann. 341 no. 4 (2008), 859–896, II. Ann. Inst. Fourier (Grenoble) 59 no. 4 (2009), 1553–1610.Google Scholar
[8] Kac, M. Can one hear the shape of a drum? Amer. Math. Monthly 73 (1966), 1–23.Google Scholar
[9] Kokotov, A. Polyhedral surfaces and the determinant of the Laplacian. Proc. Amer. Math. Soc. 141 no. 2 (2013), 725–735.Google Scholar
[10] Mazzeo, R. Elliptic theory of differential edge operators I. Comm. Partial Differential Equations 16 no. 10 (1991), 1615–1664.Google Scholar
[11] Mazzeo, R. Resolution blowups, spectral convergence and quasi-asymptotically conic spaces. Journées équations aux dérivées partielles Art. No. 8, (2006), 16 p.Google Scholar
[12] Melrose, R. The Atiyah–Patodi–Singer index theorem. Res. Not. Math. 4 (A K Peters, Ltd., 1993).Google Scholar
[13] McKean, H. P. Jr., and Singer, I. M. Curvature and the eigenvalues of the Laplacians. J. Differential Geom. 1 (1967), 43–69.Google Scholar
[14] Rowlett, J. Spectral geometry and asymptotically conic convergence. PhD. thesis (Stanford University, June 2006).Google Scholar
[15] Rowlett, J. Spectral geometry and asymptotically conic convergence. Comm. Anal. Geom. 16 no. 4 (2008), 735–798.Google Scholar
[16] Sher, D. The heat kernel on an asymptotically conic manifold. Anal. PDE 6 no. 7 (2013), 1755–1791.Google Scholar