Hostname: page-component-7479d7b7d-c9gpj Total loading time: 0 Render date: 2024-07-11T18:21:41.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometrically finite groups, Khintchine-type theorems and Hausdorff dimension

Published online by Cambridge University Press:  24 October 2008

Sanju L. Velani
Sanju L. Velani
Affiliation:
Mathematisches Institut, Bunsenstrasse 3-5, 37073 Göttingen, Germany†
Get access Rights & Permissions [Opens in a new window]

Extract

1·1. Groups of the first kind. In [11], Patterson proved a hyperbolic space analogue of Khintchine's theorem on simultaneous Diophantine approximation. In order to state Patterson's theorem, some notation and terminology are needed. Let ‖x‖ denote the usual Euclidean norm of a vector x in 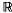k+1, k + 1-dimensional Euclidean space, and let 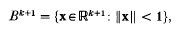be the unit ball model of k + 1-dimensional hyperbolic space with Poincaré metric ρ. A non-elementary geometrically finite group G acting on Bk + 1 is a discrete subgroup of Möb (Bk+l), the group of orientation preserving Mobius transformations preserving Bk + 1, for which there exists some convex fundamental polyhedron with finitely many faces. Since G is non-elementary, the limit set L(G) of G – the set of limit points in the unit sphere Sk of any orbit of G in Bk+1 – is uncountable. The group G is said to be of the first kind if L(G) = Sk and of the second kind otherwise.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 4 , November 1996 , pp. 647 - 662
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cassels, J. W. S.. An introduction to Diophantine approximation (Cambridge University Press, 1957).Google Scholar
[2]Dodson, M. M.. Hausdorff dimension, lower order and Khintchine's theorem in metric Diophantine approximation. J. reine angew. Math. 432 (1992), 69–76.Google Scholar
[3]Dodson, M. M., Melián, M., Pestana, D. and Velani, S. L.. Patterson measure and ubiquity. Ann. Acad. Sci. Fenn. 20: 1 (1995), 37–60.Google Scholar
[4]Dodson, M. M., Rynne, B. P. and Vickers, J. A. G.. Diophantine approximation and a lower bound for Hausdorff dimension. Mathematika 37 (1990), 59–73.CrossRefGoogle Scholar
[5]Falconer, K. J.. Fractal geometry – mathematical foundations and applications (J. Wiley, 1990).CrossRefGoogle Scholar
[6]Hill, R. and Velani, S. L.. Ergodic theory of shrinking targets. Inventiones math. 119 (1995), 175–198.CrossRefGoogle Scholar
[7]Hill, R. and Velani, S. L.. The Jarník–Besicovitch theorem for geometrically finite Kleinian groups, preprint (1994).Google Scholar
[8]Melián, M. V. and Pestana, D.. Geodesic excursions into cusps in finite volume hyperbolic manifolds. Michigan Math. J. 40 (1993), 77–93.CrossRefGoogle Scholar
[9]Melián, M. V. and Velani, S. L.. Geodesic excursions into cusps infinite volume hyperbolic manifolds. Mathematica Gottingensis 45, preprint.Google Scholar
[10]Patterson, S. J.. Lectures on measures on limit sets of Kleinian groups; in Analytic and geometrical aspects of hyperbolic space (Epstein, D. B. A., ed). LMS 111 (Cambridge University Press, 1987) 281–323.Google Scholar
[11]Patterson, S. J.. Metric Diophantine approximation of quadratic forms. In Number theory and dynamical systems (Dodson, M. M. and Vickers, J. A. G., eds.). LMS 134 (Cambridge University Press, 1989), 37–48.Google Scholar
[12]Sprindžuk, V. G.. Metric theory of Diophantine approximation. Translated by Silverman, R. A. (V. H. Winston & Sons, 1979).Google Scholar
[13]Stratmann, B.. Finer structure of limit sets of Kleinian groups. Math. Proc. Cam. Phil. Soc. 116 (1994), 57–68.CrossRefGoogle Scholar
[14]Stratmann, B.. Fractal Dimensions for the Jarník limit sets of geometrically finite Kleinian groups; the semi-classical approach. Mathematica Gottingensis 8, preprint.Google Scholar
[15]Stratmann, B. and Velani, S. L.. The Patterson measure for geometrically finite groups with parabolic elements, new and old. Proc. London Math. Soc. (3) 71 (1995), 197–220.CrossRefGoogle Scholar
[16]Sullivan, D.. Entropy, Hausdorff measures old and new, and the limit set of geometrically finite Kleinian groups. Acta Math. 153 (1984), 259–277.CrossRefGoogle Scholar
[17]Velani, S. L.. Diophantine approximation and Hausdorff dimension in Fuchsian groups. Math. Proc. Cam. Phil. Soc. 113 (1993), 343–354.CrossRefGoogle Scholar
[18]Velani, S. L.. An application of metric Diophantine approximation in hyperbolic space to quadratic forms. Publicacions mathematiques 38 (1994), 175–185.CrossRefGoogle Scholar