No CrossRef data available.
Article contents
Effective bounds on differences of singular moduli that are S-units
Published online by Cambridge University Press: 22 September 2022
Abstract
Given a singular modulus
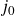 $j_0$
and a set of rational primes S, we study the problem of effectively determining the set of singular moduli j such that
$j_0$
and a set of rational primes S, we study the problem of effectively determining the set of singular moduli j such that
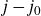 $j-j_0$
is an S-unit. For every
$j-j_0$
is an S-unit. For every
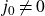 $j_0 \neq 0$
, we provide an effective way of finding this set for infinitely many choices of S. The same is true if
$j_0 \neq 0$
, we provide an effective way of finding this set for infinitely many choices of S. The same is true if
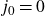 $j_0=0$
and we assume the Generalised Riemann Hypothesis. Certain numerical experiments will also lead to the formulation of a “uniformity conjecture” for singular S-units.
$j_0=0$
and we assume the Generalised Riemann Hypothesis. Certain numerical experiments will also lead to the formulation of a “uniformity conjecture” for singular S-units.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 2 , March 2023 , pp. 415 - 450
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society




