Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-09T07:13:56.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Del Pezzo surfaces over finite fields and their Frobenius traces

Published online by Cambridge University Press:  10 April 2018

BARINDER BANWAIT ,
FRANCESC FITÉ  and
DANIEL LOUGHRAN
BARINDER BANWAIT
Affiliation:
CMR Surgical, Crome Lea Business Park, Madingley Road, Cambridge, CB23 7PH. e-mail: barinder.banwait@cmrsurgical.com
FRANCESC FITÉ
Affiliation:
Departament de Matemàtiques, Universitat Politècnica de Catalunya/BGSmath Edifici Omega, C/Jordi Girona 1–3, 08034 Barcelona, Catalonia. e-mail: francesc.fite@gmail.com
DANIEL LOUGHRAN
Affiliation:
School of Mathematics, University of Manchester, Oxford Road, Manchester, M13 9PL. e-mail: daniel.loughran@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let S be a smooth cubic surface over a finite field 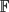$\mathbb{F}$q. It is known that #S(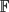$\mathbb{F}$q) = 1 + aq + q2 for some a ∈ {−2, −1, 0, 1, 2, 3, 4, 5, 7}. Serre has asked which values of a can arise for a given q. Building on special cases treated by Swinnerton–Dyer, we give a complete answer to this question. We also answer the analogous question for other del Pezzo surfaces, and consider the inverse Galois problem for del Pezzo surfaces over finite fields. Finally we give a corrected version of Manin's and Swinnerton–Dyer's tables on cubic surfaces over finite fields.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 167 , Issue 1 , July 2019 , pp. 35 - 60
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Blunk, M. Del Pezzo surfaces of degree 6 over an arbitrary field. J. Algebra 323 (2010), no. 1, 42–58.Google Scholar
[2] Bosma, W., Cannon, J. and Playoust, C. The Magma algebra system. I. The user language. J. Symbolic Comput. 24 (1997), no. 3–4, 235–265.Google Scholar
[3] Colliot-Thélène, J.-L., Karpenko, N. A. and Merkur'ev, A. S.. Rational surfaces and the canonical dimension of PGL6. Algebra i Analiz 19 (2007), no. 5, 159–178; translation in St. Petersburg Math. J. 19 (2008), no. 5, 793–804.Google Scholar
[4] Cossec, F. R. and Dolgachev, I. V. Enriques surfaces. I. Progr. Math. 76 (Birkhäuser Boston, Inc., Boston, MA, 1989).Google Scholar
[5] Deligne, P. La conjecture de Weil. II. Inst. Hautes Études Sci. Publ. Math. 52 (1980), 137–252.Google Scholar
[6] Demazure, M. Surfaces de Del Pezzo : II - Éclater n points dans ℙ2. In Séminaire sur les Singularités des Surfaces. Lecture Notes in Math. 777 (Springer, Berlin, 1980).Google Scholar
[7] Dolgachev, I.V. Classical Algebraic Geometry: a Modern View. (Cambridge University Press, Cambridge, 2012).Google Scholar
[8] Ekedahl, T. An effective version of Hilbert's irreducibility theorem. Séminaire de Théorie des Nombres, Paris 1988–1989, 241–249 Progr. Math. 91 (Birkhäuser Boston, Boston, MA, 1990).Google Scholar
[9] Ekedahl, T. One semester of elliptic curves. EMS Series of Lectures in Math., European Mathematical Society (EMS) (Zürich, 2006).Google Scholar
[10] Elsenhans, A.-S. and Jahnel, J.. Moduli spaces and the inverse Galois problem for cubic surfaces. Trans. Amer. Math. Soc. 367 (2015), no. 11, 7837–7861.Google Scholar
[11] Erné, R. Construction of a del Pezzo surface with maximal Galois action on its Picard group. J. Pure Appl. Algebra 97 (1994), no. 1, 15–27.Google Scholar
[12] Frame, J. S. The classes and representations of the groups of 27 lines and 28 bitangents. Ann. Mat. Pura Appl. (4) 32 (1951), 83–119.Google Scholar
[13] Hartshorne, R. Algebraic Geometry (Springer-Verlag, 1977).Google Scholar
[14] Hirschfeld, J. W. P. Del Pezzo surfaces over finite fields. Tensor (N.S.) 37 (1982), no. 1, 79–84.Google Scholar
[15] Hirschfeld, J. W. P. Projective Geometries Over Finite Fields. Second edition (Clarendon Press, Oxford, 1998).Google Scholar
[16] Hirschfeld, J. W. P. Finite Projective Spaces of Three Dimensions (Oxford University Press, 1985).Google Scholar
[17] Iskovskih, V. A. Minimal models of rational surfaces over arbitrary fields. Izv. Akad. Nauk SSSR Ser. Mat. 43 (1979), no. 1, 19–43, 237.Google Scholar
[18] Jahnel, J. and Loughran, D. The Hasse principle for lines on del Pezzo surfaces. Int. Math. Res. Not. 23 (2015), 12877–12919,Google Scholar
[19] Kaplan, N. Rational point counts for del Pezzo surfaces over finite fields and coding theory. Harvard Ph.D. Thesis (2013).Google Scholar
[20] Kempf, G. Algebraic varieties. London Math. Soc. Lecture Note Series, 172 (Cambridge University Press, Cambridge, 1993).Google Scholar
[21] Knecht, A. and Reyes, K. Full degree two del Pezzo surfaces over finite fields. In: Contemporary Developments in Finite Fields and Their Applications (World Scientific Press, 2016), 145–159.Google Scholar
[22] Koitabashi, M. Automorphism groups of generic rational surfaces. J. Algebra 116 (1988), no. 1, 130–142.Google Scholar
[23] Kunyavskij, A. E., Skorobogatov, A. N. and Tsfasman, M. A. Del Pezzo surfaces of degree four. Mem. de la S.M.F. 37 (1989), 1–113.Google Scholar
[24] Kuwata, M. Twenty-eight double tangent lines of a plane quartic curve with an involution and the Mordell–Weil lattices. Comment. Math. Univ. St. Pauli 54 (2005), no. 1, 17–32.Google Scholar
[25] Lang, S. and Weil, A. Number of points of varieties in finite fields. Amer. J. Math. 76, no. 4, (1954), 819–827Google Scholar
[26] Li, S. Rational points on del Pezzo surfaces of degree 1 and 2. Ph.D. Thesis, Rice University (2010). arXiv:0904.3555.Google Scholar
[27] Manin, Y. I. Cubic forms. North-Holland Mathematical Library 4 (North-Holland Publishing Co., 2nd ed. 1986).Google Scholar
[28] Poonen, B. Rational points on varieties. Graduate Stud. Math. 186 (2017).Google Scholar
[29] Rybakov, S. Zeta functions of conic bundles and del Pezzo surfaces of degree 4 over finite fields. Mosc. Math. J. 5 (2005), no. 4, 919–926, 974.Google Scholar
[30] Rybakov, S. and Trepalin, A. Minimal cubic surfaces over finite fields. Mat. Sb. 208 (2017), no. 9, 148–170.Google Scholar
[31] Salgado, C., Testa, D. and Várilly-Alvarado, A.. On the Unirationality of del Pezzo surfaces of degree two. J. Lond. Math. Soc. 90 (2014), 121–139.Google Scholar
[32] Scholl, A. J. A finiteness theorem for del Pezzo surfaces over algebraic number fields. J. Lond. Math. Soc. 32 (1985), no. 1, 31–40.Google Scholar
[33] Serre, J.-P.. Lectures on NX(p). Chapman & Hall/CRC Research Notes in Mathematics, 11 (CRC Press, Boca Raton, FL, 2012).Google Scholar
[34] Shioda, T. Theory of Mordell–Weil lattices. Proceedings of the International Congress of Mathematicians, Vol. I, II (Kyoto, 1990), 473–489, Math. Soc. Japan, Tokyo (1991).Google Scholar
[35] Skorobogatov, A. Torsors and rational points (Cambridge University press, 2001).Google Scholar
[36] Swinnerton-Dyer, H. P. F. The zeta function of a cubic surface over a finite field. Proc. Camb. Philos. Soc. 63 (1967) 55–71.Google Scholar
[37] Swinnerton-Dyer, H. P. F. Cubic surfaces over finite fields. Math. Proc. Camb. Philos. Soc. 149 (2010), 385–388.Google Scholar
[38] Trepalin, A. Minimal del Pezzo surfaces of degree 2 over finite fields. Bull. Korean Math. Soc. 54 (2017), no. 5, 1779–1801.Google Scholar
[39] Urabe, T. Calculation of Manin's invariant for del Pezzo surfaces. Math. Comp. 65 (1996), no. 213, 247–258, S15–S23.Google Scholar
[40] Urabe, T. The bilinear form of the Brauer group of a surface. Invent. Math. 125 (1996), no. 3, 557–585.Google Scholar
[41] Várilly-Alvarado, A. and Zywina, D.. Arithmetic E 8 lattices with maximal Galois action. LMS J. Comput. Math. 12 (2009), 144–165.Google Scholar