Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ellis, G.J.
and
Porter, T.
1986.
Free and projective crossed modules and the second homology group of a group.
Journal of Pure and Applied Algebra,
Vol. 40,
Issue. ,
p.
27.
Baues, Hans Joachim
and
Conduché, Daniel
1991.
On the tensor algebra of a non-abelian group and applications.
K-Theory,
Vol. 5,
Issue. 6,
p.
531.
Brown, Ronald
and
Higgins, Philip J.
1991.
The classifying space of a crossed complex.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 110,
Issue. 1,
p.
95.
Hernández, Luis Javier
and
Porter, Timothy
1992.
An embedding theorem for proper n-types.
Topology and its Applications,
Vol. 48,
Issue. 3,
p.
215.
Hernández, L. J.
and
Porter, T.
1992.
Algebraic Topology Homotopy and Group Cohomology.
Vol. 1509,
Issue. ,
p.
146.
Carrasco, P.
and
Cegarra, A.M.
1996.
(Braided) tensor structures on homotopy groupoids and nerves of (Braided) categorical groups1.
Communications in Algebra,
Vol. 24,
Issue. 13,
p.
3995.
Brown, Ronald
1996.
Homotopy theory, and change of base for groupoids and multiple groupoids.
Applied Categorical Structures,
Vol. 4,
Issue. 2-3,
p.
175.
Brown, Ronald
and
Salleh, Abdul Razak
1999.
Free Crossed Resolutions of Groups and Presentations of Modules of Identities among Relations.
LMS Journal of Computation and Mathematics,
Vol. 2,
Issue. ,
p.
28.
Tonks, A.P.
2003.
On the Eilenberg–Zilber theorem for crossed complexes.
Journal of Pure and Applied Algebra,
Vol. 179,
Issue. 1-2,
p.
199.
Brown, Ronald
2009.
Handbook of Algebra - Volume 6.
Vol. 6,
Issue. ,
p.
83.
Akça, İbrahim İlker
and
Avcıoğlu, Osman
2021.
Homotopies of crossed complex morphisms of associative R-algebras.
Georgian Mathematical Journal,
Vol. 28,
Issue. 2,
p.
163.
 of cellular chains of the universal cover
of cellular chains of the universal cover 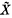 of a reduced CW-complex X. The group of operators here is the fundamental group of X.
of a reduced CW-complex X. The group of operators here is the fundamental group of X.



