No CrossRef data available.
The classification of orbits
Published online by Cambridge University Press: 24 October 2008
Extract
The present paper is concerned with a simple type of dynamical system, a system having only two freedoms and of “separable” type. The essential simplification introduced by this restriction is that the motions in the two coordinates can be discussed to some extent independently of each other. In Part I a method of classification of the possible orbits is explained. Four constants are needed to define the motion completely, but the general nature of the orbit depends on two constants suitably chosen, and the classification is effected by reference to a plane in which the two constants are taken as Cartesian coordinates. It is shewn that the plane of reference is divided into regions by critical curves, and that the orbits represented by points in the same region (each point representing a set of orbits, not a single orbit) are of the same general type. The various possible types of orbits, and their stability, in a special sense, are discussed. In Part II the theory is applied by way of illustration to a somewhat trivial example, the orbits for a particle under a central attraction proportional to the inverse (n + 1)th power of the distance. The most striking thing here is that the possible types of orbits are essentially the same for all values of n greater than 2. In Part III the theory is applied to the classical problem of a particle subject to an attraction of Newtonian type to two fixed centres, a problem of some interest in relation to the general problem of three bodies, and to some current questions in atomic dynamics. The problem is of course not a new one, but it seems that a satisfactory classification of all the possible orbits has not previously been given. It must be confessed that the complete classification for this problem is very laborious.
- Type
- Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 25 , Issue 1 , January 1929 , pp. 1 - 19
- Copyright
- Copyright © Cambridge Philosophical Society 1929
References
* But in the physical applications it is usually only the simpler case of equal attracting centres that is considered.
† There ia a discussion of the classification of the orbits in Charlier's Mechanik des Himmels, vol. I, pp. 117–163: but the conclusions there given are not entirely in agreement with those of the present paper.
* For the case of only two freedoms Stäcker's system is equivalent to Liouville's.
* The discrimination of the particular orbits of the set involves the third integration-constant, the phase-constant that appears in the primitive of
The fourth integration-constant is merely the epoch-constant, depending on the instant from which t is measured.
* The given values of h, a may represent also a set of orbits in a different part of the x, y plane: but these orbits do not change type when we cross the critical curve in question.
† For motion on x = a the graph of R (x) touches the axis of x at x = a, the curve lying below the axis in the stable and above in the unstable case. The discussion just given of the stability of the motion may be illustrated by considering the modification of the form of the graph under a small disturbance.
* For the instability arose before when x > a 1, and now this can only happen if a > a 1 and a > x > a 1.
* When n=l, 2 the differential equation of the orbit is of course integrable in circular functions.
* The curve is closed and the motion periodic if 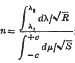 is rational: the curve is a simple closed oval curve if n = l.
is rational: the curve is a simple closed oval curve if n = l.




