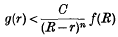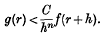Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hayman, W. K.
and
Stewart, F. M.
1954.
Real inequalities with applications to function theory.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 50,
Issue. 2,
p.
250.
1973.
Introduction to the Theory of Entire Functions.
Vol. 56,
Issue. ,
p.
186.
Alonso, Angel
Fernández, Arturo
and
Pérez, Javier
2004.
Value Distribution Theory and Related Topics.
p.
93.