Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-20T06:48:59.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak Cayley tables and generalized centralizer rings of finite groups

Published online by Cambridge University Press:  14 August 2012

STEPHEN P. HUMPHRIES  and
EMMA L. RODE
STEPHEN P. HUMPHRIES
Affiliation:
Department of Mathematics, Brigham Young University, Provo, UT 84602, USA e-mail: steve@math.byu.edu; et@math.byu.edu
EMMA L. RODE
Affiliation:
Department of Mathematics, Brigham Young University, Provo, UT 84602, USA e-mail: steve@math.byu.edu; et@math.byu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

For a finite group G we study certain rings 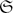(k)G called k-S-rings, one for each k ≥ 1, where 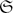(1)G is the centraliser ring Z(ℂG) of G. These rings have the property that 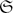(k+1)G determines 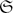(k)G for all k ≥ 1. We study the relationship of 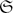(2)G with the weak Cayley table of G. We show that 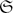(2)G and the weak Cayley table together determine the sizes of the derived factors of G (noting that a result of Mattarei shows that 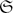(1)G = Z(ℂG) does not). We also show that 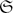(4)G determines G for any group G with finite conjugacy classes, thus giving an answer to a question of Brauer. We give a criteria for two groups to have the same 2-S-ring and a result guaranteeing that two groups have the same weak Cayley table. Using these results we find a pair of groups of order 512 that have the same weak Cayley table, are a Brauer pair, and have the same 2-S-ring.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 153 , Issue 2 , September 2012 , pp. 281 - 318
Copyright
Copyright © Cambridge Philosophical Society 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B]Bannai, E.Subschemes of some association schemes. J. Algebra 144 (1991), 167–188.CrossRefGoogle Scholar
[Br]Brauer, R.Representations of finite groups. Lectures in Modern Mathematics, Vol. I. Editor Saaty, T. L. (Wiley, New York, 1963), 133–175.Google Scholar
[Ca]Camina, A. R.Some conditions which almost characterize Frobenius groups. Israel J. Math. 31 (1978), 153–160.CrossRefGoogle Scholar
[Cur]Curtis, C. W.Pioneers of representation theory: Frobenius, Burnside, Schur and Brauer. History of Mathematics, vol. 15. (American Mathematical Society, Providence, RI; London Mathematical Society, London, 1999), pp. 287 MR1715145.CrossRefGoogle Scholar
[Fe]Feit, W.Characters of Finite Groups (W. A. Benjamin, 1967).Google Scholar
[FS]Formanek, E. and Sibley, D.The group determinant determines the group. Proc. Amer. Math. Soc. 112 (1991), 649–656.CrossRefGoogle Scholar
[Fr]Frobenius, F. G. Über vertauschbare Matrizen. S'ber. Akad. Wiss. Berlin (1896), 601–614.Google Scholar
[Ha]Hall, M. Jr.The Theory of Groups (Chelsea Publishing Co., New York, 1976).Google Scholar
[HoJ]Hoehnke, H.-J. and Johnson, K. W.3-characters are sufficient for the group determinant. Second International Conference on Algebra (Barnaul, 1991), Contemp. Math. vol. 184 (Amer. Math. Soc., Providence, RI, 1995), 193–206.Google Scholar
[Hu]Humphries, S. P.Weak Cayley table groups. J. Algebra 216 (1999), 135–158.CrossRefGoogle Scholar
[HJ]Humphries, S. P. and Johnson, K. W.Fusions of character tables and Schur rings of Abelian groups. Comm. Algebra 21 (2008), 1437–1460.CrossRefGoogle Scholar
[HJK]Humphries, S. P., Johnson, K. W. and Kerby, B.Fusions of character tables III: fusions of cyclic groups and a generalization of a condition of Camina. Israel J. Math. 178 (2010), 325–348.CrossRefGoogle Scholar
[J]Johnson, K. W.On the group determinant. Math. Proc. Camb. Phil. Soc. 109 (1991), 299–311.CrossRefGoogle Scholar
[JMS]Johnson, K. W., Mattarei, S. and Sehgal, S. K.Weak Cayley tables. J. London Math. Soc. 61 (2000), 395–411.CrossRefGoogle Scholar
[JSe]Johnson, K. W. and Sehgal, S. K.The 2-character table does not determine a group. Proc. Amer. Math. Soc. 119 (1993), 1021–1027.CrossRefGoogle Scholar
[JS]Johnson, K. W. and Smith, J. D. H.Characters of finite quasigroups. III. Quotients and fusion. European J. Combin. 10 (1989), 47–56.CrossRefGoogle Scholar
[KR]Kimmerle, W. and Roggenkamp, K. W.Non-isomorphic groups with isomorphic spectral tables and Burnside matrices. Chinese Ann. Math. Ser. B 15 (1994), 273–282.Google Scholar
[LP]Lux, K. and Pahlings, H.Computational aspects of representation theory of finite groups. II. Algorithmic algebra and number theory (Heidelberg, 1997), (Springer, Berlin, 1999), pp. 381–397.Google Scholar
[MA]Bosma, W. and Cannon, J.MAGMA University of Sydney, (1994).Google Scholar
[MS]Mann, A. and Scoppola, C. M.On p-groups of Frobenius type. Arch. Math. (Basel) 56 (1991), 320–332.CrossRefGoogle Scholar
[Ma]Mansfield, R.A group determinant determines its group. Proc. Amer. Math. Soc. 116 (1992), 939–941.CrossRefGoogle Scholar
[M1]Mattarei, S.An example of p-groups with identical character tables and different derived lengths, Arch. Math. (Basel), 62 (1994), 12–20.CrossRefGoogle Scholar
[M2]Mattarei, S.On character tables of wreath products. J. Algebra 175 (1995), 157–178.CrossRefGoogle Scholar
[M3]Mattarei, S.Character tables and metabelian groups. J. London Math. Soc. 46 (1992), 92–100.CrossRefGoogle Scholar
[Os]Osin, D. V. Small cancellations over relatively hyperbolic groups and embedding theorems. arXiv:math/0411039v2.Google Scholar
[R]Roggenkamp, K. W.From Dedekind's group determinant to the isomorphism problem. C. R. Math. Acad. Sci. Soc. R. Can. 21 (1999), 97–126.Google Scholar
[Sch]Schur, I. Zur Theorie der einfach transitiven Permutationsgruppen. Sitz. Preuss. Akad. Wiss. Berlin, Phys-math Klasse (1933), 598–623.Google Scholar
[Sc]Scott, W. R. Group Theory (Dover, 1987).Google Scholar
[S]Smith, J. D. H. An Introduction to Quasigroups and their Representations. Studies in Advanced Mathematics (Chapman and Hall/CRC, Boca Raton, FL, 2007), pp. 340.Google Scholar
[Vaz]Vazirani, M. J.Extending Frobenius' higher characters Sci. Math. Japan. 58 (2003), 169–182.Google Scholar
[Wie]Wielandt, H.Finite Permutation Groups (Academic Press, New York-London, 1964) x+114.Google Scholar