No CrossRef data available.
The Parseval formulae for monotonic functions. IV
Published online by Cambridge University Press: 24 October 2008
Extract
This note contains two counter-examples which have a bearing on work published in earlier papers (1, 2, 3) of the sequence. It has been shown that the Parseval formulae for Fourier cosine and sine transforms,
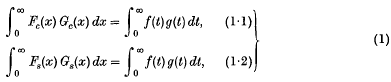
hold in a number of cases when two of the functions concerned are monotonic, and that there are corresponding results for Fourier series. In some of these theorems, the existence of one side of the relevant equation (in the ordinary finite sense) is postulated; others contain no such existence condition, and show that either both sides are finite and equal, or both sides are ‘ + ∞’. In the case of sine transforms, we always obtain theorems of the second type (which is clearly the stronger); but cosine transforms are more troublesome. The first of the examples which we shall give is designed to show that the cosine formula is not always true in the ‘finite or infinite’ sense when two of the functions are monotonic.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 49 , Issue 2 , April 1953 , pp. 218 - 229
- Copyright
- Copyright © Cambridge Philosophical Society 1953




