On the periods of the exponential and elliptic functions
Published online by Cambridge University Press: 24 October 2008
Extract
Let ℘ be a Weierstrass elliptic function satisfying the differential equation
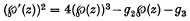
and let ζ(z) be the associated Weierstrass ζ-function satisfying 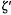 (z) = −℘(z). Corresponding to a pair of fundamental periods ω1, ω2 of ℘(z), there is a pair of quasi-periods η1, η2 of ζ(z) defined by
(z) = −℘(z). Corresponding to a pair of fundamental periods ω1, ω2 of ℘(z), there is a pair of quasi-periods η1, η2 of ζ(z) defined by
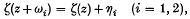
and we have ηi = 2ζ(ωi/2) for i = 1, 2.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 73 , Issue 2 , March 1973 , pp. 339 - 350
- Copyright
- Copyright © Cambridge Philosophical Society 1973
References
REFERENCES
- 1
- Cited by




