Hostname: page-component-84b7d79bbc-2l2gl Total loading time: 0 Render date: 2024-07-26T12:26:25.705Z Has data issue: false hasContentIssue false
  • English
  • Français

On factorials which are products of factorials

Published online by Cambridge University Press:  01 November 2007

FLORIAN LUCA
FLORIAN LUCA*
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México, C.P. 58089, Morelia, Michoacán, México. email: fluca@matmor.unam.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

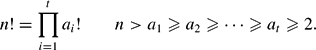In this paper, we look at the Diophantine equation (0.1) Under the ABC conjecture, we show that it has only finitely many nontrivial solutions. Unconditionally, we show that the set of n for which the above equation admits an integer solution a1,. . .,at is of asymptotic density zero.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 143 , Issue 3 , November 2007 , pp. 533 - 542
Copyright
Copyright © Cambridge Philosophical Society 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Berend, D. and Harmse, J. E.. On polynomial-factorial Diophantine equations. Trans. Amer. Math. Soc. 358 (2006), 1741–1779.CrossRefGoogle Scholar
[2]Berend, D. and Osgood, C. F.. On the equation P(x) = n! and a question of Erdős'. J. Number Theory 42 (1992), 189–193.CrossRefGoogle Scholar
[3]Erdős, P. and Selfridge, J. L.. The product of consecutive integers is never a power. Illinois J. Math. 19 (1975), 292–301.CrossRefGoogle Scholar
[4]Erdős, P.. Some problem and results and the irrationality of the sum of infinite series. J. Math. Sci. 10 (1975), 1–7.Google Scholar
[5]Erdős, P. and Graham, R. L.. Old and new problems and results in combinatorial number theory. Monographie No. 28L'Enseignement Math. Genève (1980).Google Scholar
[6]Evertse, J. H.. On equations in S-units and the Thue-Mahler equation. Invent. Math. 75 (1984), 561–584.CrossRefGoogle Scholar
[7]Laishram, S. and Shorey, T. N.. Number of prime divisors in a product of consecutive integers. Acta Arith. 113 (2004), 327–341.CrossRefGoogle Scholar
[8]Luca, F.. The Diophantine equation P(x) = n! and a result M. Overholt. Glas. Mat. Ser. III 37 (57) (2002), 269–273.Google Scholar
[9]Matveev, E. M.. An explicit lower bound for a homogeneous rational linear form in logarithms of algebraic numbers, II. Izv. Ross. Akad. Nauk Ser. Mat. 64 (2000), 125–180. English transl. in Izv. Mat. 64 (2000), 1217–1269.Google Scholar
[10]Overholt, M.. The Diophantine equation n! + 1 = m 2. Bull. London Math. Soc. 25 (1993), 104.CrossRefGoogle Scholar