Curvature, causality and completeness in space-times with causally complete spacelike slices
Published online by Cambridge University Press: 24 October 2008
Extract
Let S be a spacelike slice (defined formally in Section 2) in a space-time M. We will say that S is future causally complete in M if for each p ε J+(S) the closure in S of the set J-(p) ∩ S is compact. Define past causal completeness time-dually. Then S is causally complete if it is both future and past causally complete. A compact spacelike slice is necessarily causally complete, as is any Cauchy surface, but the concept of causal completeness is much broader than either of these two conditions. For example the slices t = const. ≠ 0 in the space-time obtained by removing the origin from Minkowski space are causally complete, although they are neither Cauchy nor compact. The slice t = 0 in the previous example and the hyperboloid 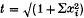 in Minkowski space (where (t, x1, …, xn) are standard inertial coordinates) are examples of slices which are not causally complete. Physically speaking, an edgeless slice S is future causally complete if the information from S which reaches a point in the future of S comes from a finite nonsingular region in S. The Maximal Reissner-Nordstrom space-time is a well-known example in which this finiteness condition is not fulfilled by any of its asymptotically flat partial Cauchy surfaces. Indeed for any such partial Cauchy surface S, J-(p) ∩ S is non-compact for any p ε H+(S). However, as has been discussed in the literature (e.g. [17], p. 625 f), it is believed that the Cauchy horizon in this situation is unstable with respect to perturbations of the initial data on S.
in Minkowski space (where (t, x1, …, xn) are standard inertial coordinates) are examples of slices which are not causally complete. Physically speaking, an edgeless slice S is future causally complete if the information from S which reaches a point in the future of S comes from a finite nonsingular region in S. The Maximal Reissner-Nordstrom space-time is a well-known example in which this finiteness condition is not fulfilled by any of its asymptotically flat partial Cauchy surfaces. Indeed for any such partial Cauchy surface S, J-(p) ∩ S is non-compact for any p ε H+(S). However, as has been discussed in the literature (e.g. [17], p. 625 f), it is believed that the Cauchy horizon in this situation is unstable with respect to perturbations of the initial data on S.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 2 , March 1986 , pp. 367 - 375
- Copyright
- Copyright © Cambridge Philosophical Society 1986
References
REFERENCES
- 22
- Cited by


