Articles
Linear and non-linear models for national health expenditures in the USA
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 193-197
-
- Article
- Export citation
Blocks of decimal digits
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 198-202
-
- Article
- Export citation
All parabolas through three non-collinear points
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 203-209
-
- Article
- Export citation
Rational arc length
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 210-225
-
- Article
- Export citation
Can our coinage system be improved?
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 226-232
-
- Article
- Export citation
Tethering in pastures new
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 233-245
-
- Article
- Export citation
From dawn to dusk
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 246-256
-
- Article
- Export citation
The existence of triangles, tetrahedra, and higher-dimensional simplices with prescribed exradii
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 257-263
-
- Article
- Export citation
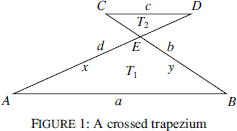
Metric relations in crossed trapezia
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 264-269
-
- Article
- Export citation
Central force fields and Kepler's laws
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 270-279
-
- Article
- Export citation
The seven circles theorem revisited
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 280-301
-
- Article
- Export citation
Other
Growing The Gazette
-
- Published online by Cambridge University Press:
- 18 June 2018, p. 301
-
- Article
- Export citation
Matter for Debate
The importance of characterisations in geometry
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 302-307
-
- Article
- Export citation
Notes
102.20 The sum of the first n cubes is a square – two Proofs without Words
-
- Published online by Cambridge University Press:
- 18 June 2018, p. 308
-
- Article
- Export citation
102.21 An addendum to Estermann's proof of the irrationality of
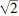
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 308-309
-
- Article
- Export citation
102.22 Proof without Words: sums of sums of factorials is one less than a factorial: inductive step
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 309-310
-
- Article
- Export citation
102.23 A visual proof that
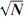 is irrational
is irrational
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 311-312
-
- Article
- Export citation
102.24 Area of a circle via the Fundamental Theorem of Calculus
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 312-314
-
- Article
- Export citation
102.25 On an alternative formula for the area of a spherical cap
-
- Published online by Cambridge University Press:
- 18 June 2018, pp. 314-316
-
- Article
- Export citation
102.26 An ad hoc limiting process
-
- Published online by Cambridge University Press:
- 18 June 2018, p. 317
-
- Article
- Export citation




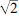 , although they might, so far as I knew, have been consecutive digits of either number in some section remote from the decimal point.
, although they might, so far as I knew, have been consecutive digits of either number in some section remote from the decimal point.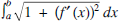 gives the length of the curve
gives the length of the curve 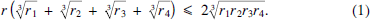
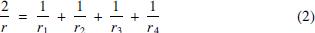
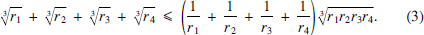
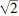
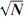 is irrational
is irrational