Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-20T22:27:29.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Partitions of primes and other sequences

Published online by Cambridge University Press:  01 August 2016

K. Robin McLean
K. Robin McLean*
Affiliation:
Dept of Education, University of Liverpool, PO Box 147, Liverpool L69 3BX
Get access Rights & Permissions [Opens in a new window]

Extract

Let p1, p2, p3, … be the sequence of primes. Take any integer n ⩾ 2 and partition the set {p1p2, … , pn} into two non-empty subsets A and B. Let PA be the product of primes in A and PB be the product of primes in B. No partition exists with PA = PB, because of the uniqueness of prime factorisation, but Fernando Castro’s neat result in [1] asserts that for each n there is a partition for which 1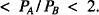

Type
Articles
Information
The Mathematical Gazette , Volume 89 , Issue 514 , March 2005 , pp. 15 - 21
Copyright
Copyright © The Mathematical Association 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Fernando Castro, G., More on the sequence of prime numbers, Math. Gaz. 86 (July 2002) pp. 264–265.Google Scholar
2. Ribenboim, P., The book of prime number records, Springer-Verlag (1988).Google Scholar
3. Hardy, G.H., A course of pure mathematics (10th edn.), Cambridge University Press (1952).Google Scholar