No CrossRef data available.
Article contents
xy = cos (x + y) and other implicit equations that are surprisingly easy to plot
Published online by Cambridge University Press: 15 February 2024
Extract
The following equations relate y only implicitly to x:(1)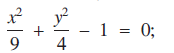 (2)
(2)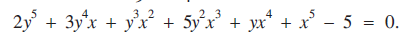 In both equations, y is a function of x for a continuous range of (x, y) values in the real x-y plane. (1) represents an ellipse. (2) has been designed by the author to have a solution in the real x-y plane at (−1, 2), and because the function on the left-hand side of (2) meets certain conditions regarding continuity and partial differentiability there must be a line of points in the real x-y plane satisfying (2) and passing continuously through (−1, 2) [1, pp. 23-28].
In both equations, y is a function of x for a continuous range of (x, y) values in the real x-y plane. (1) represents an ellipse. (2) has been designed by the author to have a solution in the real x-y plane at (−1, 2), and because the function on the left-hand side of (2) meets certain conditions regarding continuity and partial differentiability there must be a line of points in the real x-y plane satisfying (2) and passing continuously through (−1, 2) [1, pp. 23-28].
- Type
- Articles
- Information
- Copyright
- © The Authors, 2024 Published by Cambridge University Press on behalf of The Mathematical Association





