No CrossRef data available.
Article contents
Computing indefinite integrals by difference equations
Published online by Cambridge University Press: 11 October 2023
Extract
In teaching mathematics to first-year undergraduates, and thus in the appropriate calculus textbooks, the task of calculating an integral that satisfies a specific first-order or second-order recurrence relation often appears. These relations are obtained mainly by applying the method of integration by parts. Calculating such integrals is usually tedious, especially for an integer n > 2, time-consuming, and presents the possibility of making a large number of errors when computing involves multiple iterative steps. In [1], it is shown that in two cases (Theorems 2.1. and 2.3), the process of calculating integrals satisfying first-order recurrence relations can be performed quickly using easily memorised closed-form formulas for corresponding primitive functions. The question can rightly be asked whether there is a faster way to calculate other integrals of this type. In this paper, our goal is to give an affirmative answer to such a question, though without convering all situations. Since each recurrence relation is equivalent to a difference equation of the same order, the calculation of integrals mentioned above can be reduced to solving the corresponding difference equations. Since every first-order or second-order linear difference equation is solvable, it follows that for every integral which can be reduced to a first- order or second-order recurrence formula, it is possible to find corresponding primitive functions directly. Sometimes such a procedure is much faster than iterative solving of the integral. Closed-form formulas for the integrals discussed in the following sections are not unknown (see [2]). However, here our goal is to present the idea of computing indefinite integrals using difference equations. We will discuss it in more detail in Section 2. In Section 3, we discuss the application of the results obtained to calculate several improper integrals and the application of some of them in different sciences. An exciting example of such an application is the integral 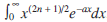 , which in the case n = 1 is used in the kinetic theory of gases, particularly in the Maxwell-Boltzmann distribution of gas molecules by energies (see Remark 4). Also, we compare the formulas obtained by the method of difference equations with the formulas obtained using Wolfram Alpha software (see Remark 5).
, which in the case n = 1 is used in the kinetic theory of gases, particularly in the Maxwell-Boltzmann distribution of gas molecules by energies (see Remark 4). Also, we compare the formulas obtained by the method of difference equations with the formulas obtained using Wolfram Alpha software (see Remark 5).
- Type
- Articles
- Information
- Copyright
- © The Authors, 2023 Published by Cambridge University Press on behalf of The Mathematical Association





