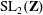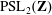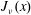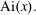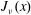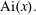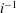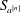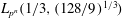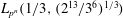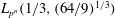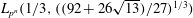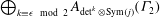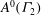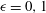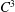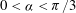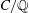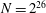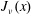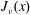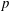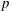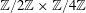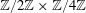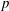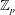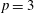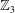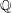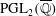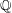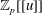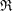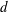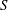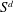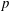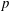Research Article
Congruence testing for odd subgroups of the modular group
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 206-208
-
- Article
-
- You have access
- Export citation
Hyper-and-elliptic-curve cryptography
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 181-202
-
- Article
-
- You have access
- Export citation
Finding roots in
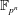 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 203-217
-
- Article
-
- You have access
- Export citation
Approximations for the Bessel and Airy functions with an explicit error term
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 209-225
-
- Article
-
- You have access
- Export citation
Traps to the BGJT-algorithm for discrete logarithms
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 218-229
-
- Article
-
- You have access
- Export citation
A note on magnitude bounds for the mask coefficients of the interpolatory Dubuc–Deslauriers subdivision scheme
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 226-232
-
- Article
-
- You have access
- Export citation
The multiple number field sieve for medium- and high-characteristic finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 230-246
-
- Article
-
- You have access
- Export citation
A note on uniform approximation of functions having a double pole
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 233-244
-
- Article
-
- You have access
- Export citation
Evaluating
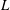 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$-functions with few known coefficients
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$-functions with few known coefficients
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 245-258
-
- Article
-
- You have access
- Export citation
On the computation of the determinant of vector-valued Siegel modular forms
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 247-256
-
- Article
-
- You have access
- Export citation
A symmetric
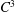 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 259-272
-
- Article
-
- You have access
- Export citation
Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 257-273
-
- Article
-
- You have access
- Export citation
On the Bessel function
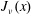 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}J_\nu (x)$ in the transition region
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}J_\nu (x)$ in the transition region
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 273-281
-
- Article
-
- You have access
- Export citation
Tracking
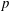 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-adic precision
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-adic precision
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 274-294
-
- Article
-
- You have access
- Export citation
High-rank elliptic curves with torsion
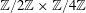 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}$ induced by Diophantine triples
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}$ induced by Diophantine triples
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 282-288
-
- Article
-
- You have access
- Export citation
Class number calculation using Siegel functions
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 295-302
-
- Article
-
- You have access
- Export citation
On the units generated by Weierstrass forms
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 303-313
-
- Article
-
- You have access
- Export citation
On the beta expansion of Salem numbers of degree 8
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 289-301
-
- Article
-
- You have access
- Export citation
A census of quadratic post-critically finite rational functions defined over
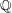 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2014, pp. 314-329
-
- Article
-
- You have access
- Export citation
Linear algebra over
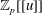 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 302-344
-
- Article
-
- You have access
- Export citation