Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-21T15:36:03.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Nilpotent-independent sets and estimation in matrix algebras

Part of: Probabilistic methods in group theory

Published online by Cambridge University Press:  01 May 2015

Brian P. Corr ,
Tomasz Popiel  and
Cheryl E. Praeger
Brian P. Corr
Affiliation:
School of Mathematics and Statistics, The University of Western Australia, Australia email brian.p.corr@gmail.com Current address: Departamento de Matemática, Instituto de Ciências Exatas, Universidade Federal de Minas Gerais, Av. Antônio Carlos, 6627, 31270-901 Belo Horizonte, MG, Brazil
Tomasz Popiel
Affiliation:
School of Mathematics and Statistics, The University of Western Australia, Australia email tomasz.popiel@uwa.edu.au
Cheryl E. Praeger
Affiliation:
School of Mathematics and Statistics, The University of Western Australia, Australia King Abdullaziz University, Jeddah, Saudi Arabia email cheryl.praeger@uwa.edu.au

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Efficient methods for computing with matrices over finite fields often involve randomised algorithms, where matrices with a certain property are sought via repeated random selection. Complexity analyses for such algorithms require knowledge of the proportion of relevant matrices in the ambient group or algebra. We introduce a method for estimating proportions of families 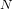$N$ of elements in the algebra of all 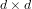$d\times d$ matrices over a field of order $q$, where membership of a matrix in 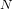$N$ depends only on its ‘invertible part’. The method is based on the availability of estimates for proportions of certain non-singular matrices depending on 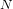$N$, so that existing estimation techniques for non-singular matrices can be used to deal with families containing singular matrices. As an application, we investigate primary cyclic matrices, which are used in the Holt–Rees MEATAXE algorithm for testing irreducibility of matrix algebras.

MSC classification

Primary: 20P05: Probabilistic methods in group theory
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 18 , Issue 1 , 2015 , pp. 404 - 418
Copyright
© The Author(s) 2015 

References

Carter, R. W., Finite groups of Lie type: conjugacy classes and complex characters (John Wiley, Chichester, 1993).Google Scholar
Corr, B. P., ‘Estimation and computation with matrices over finite fields’, PhD Thesis, The University of Western Australia, 2014.CrossRefGoogle Scholar
Corr, B. P. and Praeger, C. E., ‘Primary cyclic matrices in irreducible matrix subalgebras’, Preprint, 2014, arXiv:1401.1598.Google Scholar
Dietrich, H., Leedham-Green, C. R. and Lübeck, F., ‘Constructive recognition of classical groups in even characteristic’, J. Algebra 391 (2013) 227–255.CrossRefGoogle Scholar
Fulman, J., Neumann, P. M. and Praeger, C. E., ‘A generating function approach to the enumeration of matrices in classical groups over finite fields’, Mem. Amer. Math. Soc. 176 (2005) 1–90.Google Scholar
Gerstenhaber, M., ‘On the number of nilpotent matrices with coefficients in a finite field’, Illinois J. Math. 5 (1961) 330–333.CrossRefGoogle Scholar
Glasby, S. P., ‘The meat-axe and f-cyclic matrices’, J. Algebra 300 (2006) 77–90.CrossRefGoogle Scholar
Glasby, S. P. and Praeger, C. E., ‘Towards an efficient Meat-Axe algorithm using f-cyclic matrices: the density of uncyclic matrices in M (n, q)’, J. Algebra 322 (2009) 766–790.CrossRefGoogle Scholar
Hartley, B. and Hawkes, T. O., Rings, modules and linear algebra (Chapman & Hall, London, 1980).Google Scholar
Holt, D. F. and Rees, S., ‘Testing modules for irreducibility’, J. Aust. Math. Soc. Ser. A 57 (1994) 1–16.CrossRefGoogle Scholar
Ivanyos, G. and Lux, K., ‘Treating the exceptional cases of the MeatAxe’, Exp. Math. 9 (2000) 373–381.CrossRefGoogle Scholar
Lehrer, G. I., ‘Rational tori, semisimple orbits and the topology of hyperplane complements’, Comment. Math. Helv. 67 (1992) 226–251.CrossRefGoogle Scholar
Lehrer, G. I., ‘The cohomology of the regular semisimple variety’, J. Algebra 199 (1998) 666–689.CrossRefGoogle Scholar
Lübeck, F., Niemeyer, A. C. and Praeger, C. E., ‘Finding involutions in finite Lie type groups of odd characteristic’, J. Algebra 321 (2009) 3397–3417.CrossRefGoogle Scholar
Neumann, P. M. and Praeger, C. E., ‘Cyclic matrices over finite fields’, J. Lond. Math. Soc. (2) 52 (1995) 263–284.CrossRefGoogle Scholar
Neumann, P. M. and Praeger, C. E., ‘Cyclic matrices and the meataxe’, Groups Comput. 3 (2001) 291–300.Google Scholar
Neunhoeffer, M., Seress, Á., Ankaralioglu, N., Brooksbank, P., Celler, F., Howe, S., Law, M., Linton, S., Malle, G., Niemeyer, A. C., O’Brien, E. A. and Roney-Dougal, C. M., ‘recog. A collection of group recognition methods’, ver. 1.2. http://gap-system.github.io/recog/.Google Scholar
Neunhöffer, M. and Seress, Á., ‘Constructive recognition of SL $(n,q)$ in its natural representation’, in preparation.Google Scholar
Niemeyer, A. C., Pannek, S. B. and Praeger, C. E., ‘Irreducible linear subgroups generated by pairs of matrices with large irreducible submodules’, Arch. Math. 98 (2012) 105–114.CrossRefGoogle Scholar
Niemeyer, A. C., Popiel, T. and Praeger, C. E., ‘On proportions of pre-involutions in finite classical groups’, J. Algebra 324 (2010) 1016–1043.CrossRefGoogle Scholar
Niemeyer, A. C., Popiel, T. and Praeger, C. E., ‘Abundant p-singular elements in finite classical groups’, J. Algebra 408 (2014) 189–204.CrossRefGoogle Scholar
Niemeyer, A. C. and Praeger, C. E., ‘A recognition algorithm for classical groups over finite fields’, Proc. Lond. Math. Soc. (3) 77 (1998) 117–169.CrossRefGoogle Scholar
Niemeyer, A. C. and Praeger, C. E., ‘Estimating proportions of elements in finite groups of Lie type’, J. Algebra 324 (2010) 122–145.CrossRefGoogle Scholar
Niemeyer, A. C. and Praeger, C. E., ‘Elements in finite classical groups whose powers have large 1-eigenspaces’, Discrete Math. Theor. Comput. Sci. 16 (2014) 303–312.Google Scholar
Parker, R. A., ‘The computer calculation of modular characters (the meat-axe)’, Computational group theory (Durham, 1982) (Academic Press, London, 1984) 267–274.Google Scholar
Wall, G. E., ‘On the conjugacy classes in the unitary, symplectic and orthogonal groups’, J. Aust. Math. Soc. 3 (1963) 1–62.CrossRefGoogle Scholar