1. INTRODUCTION
This paper focuses on the research of physical processes partly related to the shock ignition (SI) (Scherbakov, Reference Scherbakov1983) that is one of the most perspective methods for targets ignition in inertial confinement fusion (ICF). This approach requires fulfillment of strict requirements for parameters of igniting shock wave and conditions of its generation. Namely, the pressure of igniting shock wave excited by laser spike action on ICF target preliminary compressed to the density of 10 g/cm3 should not be smaller than 300 Mbar, and at the same time, the laser spike intensity and duration should vary in quite narrow ranges of 1–10 PW/cm2 and 200–500 ps, respectively (Scherbakov, Reference Scherbakov1983; Betti et al., Reference Betti, Zhou, Anderson, Perkins, Theobald and Solodov2007; Ribeyre et al., Reference Ribeyre, Nikolai, Schurtz, Olazabal-Loume, Breil, Maire, Feugeas, Hallo and Tikhonchuk2008). Interaction of laser pulses at the above mentioned relatively high intensities with the plasma is strongly affected by non-collisional absorption mechanisms leading to a generation of fast super-thermal electrons. Therefore, the effects of the fast electron energy transport on the ablation pressure forming, shock wave generation and on the target compression belong to the most important problems in SI concept. In addition, the fast electron energy transfer may lead to a preheating of the target, which results in a decreased target compression.
To eliminate the target preheating, the ICF investigations are usually carried out under conditions, which avoid the generation of fast electrons. In the presence of the resonance absorption of the laser radiation, such conditions correspond to relatively small values of the parameter I Lλ2 (I L and λ — intensity and wavelength of laser radiation), which should not exceed the value of 1014 Wμm2/cm2. In the middle of the 1980s, analyses of experimental results (McCall et al., Reference McCall1983; Tan et al., Reference Tan, McCall, Kopp, Ganley and van Hulsteyn1983) concerning the compression of spherical targets by a long-wavelength radiation CO2 lasers have shown that for I Lλ2 ≈ 1015–17 Wμm2/cm2 and the laser energy above 100 kJ, the dimensional parameters of ICF target and a range of the fast electrons can be chosen in such a way to exclude preheating of the compressed part of the target (Volosevich & Rozanov, Reference Volosevich and Rozanov1981; Gus'kov et al., Reference Gus'kov, Zverev and Rozanov1983; Reference Gus'kov, Zverev and Sklizkov1987). It was also shown that under these conditions the fast electron energy transfer from the critical density region to more dense plasma areas increases the ablation pressure and thereby plays a positive role in the target compression. Recent theoretical studies (Gus'kov et al., Reference Gus'kov, Ribeyre and Touati2012) of the interaction of mono energetic electron beams with particle energy of 30–100 keV related to the laser intensities of 1–10 PW/cm2 with planar targets demonstrated a possibility to achieve the ablation pressure above 300 Mbar and the transfer up to 10% of the beam energy to the igniting shock wave during the period of 200–500 ps.
At the current stage of the ICF research, a lot of attention is devoted to a development of the SI approach. First of all, the results of experiments with spherical targets performed on the OMEGA laser (Theobald et al., Reference Theobald, Betti and Stoeckl2008; Reference Theobald, Nora and Lafon2012) at different variants of spatial configuration and temporal adjustment of 60 laser beams should be mentioned. In those experiments, the temperature of fast electrons, being a result of absorption of a petawatt per square centimeter spike of the laser pulse in the extended plasma, was measured to be on the level of 30 keV. A fraction of the laser energy scattered by the stimulated plasma processes was determined, too. These measurements confirmed the conclusions of numerical calculations (Theobald et al., Reference Theobald, Betti and Stoeckl2008; Reference Theobald, Nora and Lafon2012; Klimo et al., Reference Klimo, Tikhonchuk and Rebeyre2011) relating the generation of fast electrons in the low density plasma to non-collisional absorption of the laser light due to Raman scattering and two-plasmon decay. Additionally, a neutron yield enhancement induced by an action of the petawatt per square centimeter spike of the laser pulse was demonstrated. The analysis of these experimental data allowed us to conclude that the increased energy transfer to the target is connected with the fast electron contribution.
Most of the SI experiments are carried out using planar targets (Laboratory for Laser Energetics, 2012; Jacquemot et al., Reference Jacquemot, Amiranoff and Baton2011; Batani et al., Reference Batani, Baton, Perez, Gizzi, Koester, Labate, Honrubia, Antonelli, Morace, Volpe, Santos, Schurtz, Hulin, Ribeyre, Fourment, Nicolai, Vauzour, Gremillet, Nazarov, Pasley, Richetta, Lancaster, Spindloe, Tolley, Neely, Kozlová, Nejdl, Rus, Wolowski, Badziak and Dorchies2011). The main objectives of these investigations are the non-collisional mechanisms of absorption and scattering of the laser radiation in the extended plasma, fast electron generation, and shock wave excitation. It is worth mentioning that in the planar experiments (Laboratory for Laser Energetics, 2012) carried out on the OMEGA laser, where the third harmonic laser radiation with the intensity of 1.2 PW/cm2 and the pulse duration about 500 ps affected the plasma with a dimension of 350 µm, the 1.8% efficiency of the laser energy transformation into fast electrons with the temperature of 70 keV was achieved. The ablation pressure of 70 Mbar, determined by the measurements of the shock wave velocity in a solid part of the target, is the maximum value obtained hitherto in the SI experiments.
From a point of view of practical realization of the SI method, the essential questions related to the fast electron energy transport can be divided into two groups. The first one is the preheating of the target due to the direct fast electron energy transport into the compressed matter. The second one concerns the influence of the fast electron energy transfer in the evaporated part of the target on the ablation pressure formation and an efficient energy coupling to the shock wave. In this paper, the second group of questions was investigated in the frame of experiments where the planar Al or Cu targets were irradiated by one beam of the Prague Asterix Laser System (PALS) iodine laser. This work is a direct continuation of our experimental studies (Gus'kov et al., Reference Gus'kov, Borodziuk and Kalal2004; Reference Gus'kov, Kasperczuk, Pisarczyk, Borodziuk, Kalal, Limpouch, Ullschmied, Krousky, Masek, Pfeifer, Rohlena, Skala and Pisarczyk2006), which demonstrated that both the ablation pressure and the fast electron-to-shock wave energy transfer efficiency grow using the relatively short wavelength of the first harmonic radiation of the PALS laser. Intentionally, chosen conditions of the experiments provided a possibility to use either large intensities of several tens of PW/cm2 or low intensities with small values of I Lλ2 where the role of fast electrons is irrelevant. Bearing in mind the PALS laser pulse duration of 250 ps, it is worth mentioning that for the intensity range of 1–10 PW/cm2 our target irradiation conditions differ from those characteristic for the SI laser spike only due to the application of the single laser beam acting directly on a solid target surface. According to the SI concept, the igniting shock wave is generated by the action of the laser spike on the extended low density plasma produced by the first nanosecond part of the laser pulse in the stage of the preliminary compression of the ICF target. This difference in the energy deposition conditions relates to different mechanisms of the fast electrons generation. The results of numerical calculations (being a part of this work) have shown that in the case of non-extended plasma the fast electrons are generated due to the target normal sheet acceleration mechanism of the charge separation close to the area of critical plasma surface, while in the case of the SI extended plasmas the fast electrons are generated due to stimulated parametric processes in lower density plasma (Theobald et al., Reference Theobald, Betti and Stoeckl2008; Reference Theobald, Nora and Lafon2012; Klimo et al., Reference Klimo, Tikhonchuk and Rebeyre2011; LLE Review 2012; Jacquemot et al., Reference Jacquemot, Amiranoff and Baton2011; Batani et al., Reference Batani, Baton, Perez, Gizzi, Koester, Labate, Honrubia, Antonelli, Morace, Volpe, Santos, Schurtz, Hulin, Ribeyre, Fourment, Nicolai, Vauzour, Gremillet, Nazarov, Pasley, Richetta, Lancaster, Spindloe, Tolley, Neely, Kozlová, Nejdl, Rus, Wolowski, Badziak and Dorchies2011). Nevertheless as shown below, the average energy of fast electrons in the PALS experiment is close to that measured in the OMEGA laser experiments (Theobald et al., Reference Theobald, Betti and Stoeckl2008; Reference Theobald, Nora and Lafon2012) and also to the values anticipated for the SI conditions (Klimo et al., Reference Klimo, Tikhonchuk and Rebeyre2011). A part of experiments described in this paper was carried out with a tightly focused laser beam the intensity of which was close to the SI laser spike. In such experiments, the ablation of the target material is not planar, therefore, the interpretation of the experimental results was based on numerical simulations by two-dimensional (2D) hydrodynamic code ATLANT-HE and on theoretical analysis using the 2D analytical model specially developed in the frames of this paper. To determine the density and temperature of the plasma, three-frame interferometry and X-ray spectroscopy techniques were used. The laser energy transferred to the solid target was determined via measurements of the crater volume of crater in the target.
In Section 2, the experimental set-up and the results of measurements are presented. Section 3 describes a 2D numerical modeling of experiments. In Section 4, a 2D analytical model of the laser-produced plasma taking into account the fast-electron energy transport and a model of the energy transfer to the shock wave propagating in the solid part of the target are presented. Simultaneously, the experimental and theoretical results are discussed. Finally, the conclusions concerning the efficiency of the energy transfer from the plasma plume to the shock wave and the role of fast electrons in this process are formulated in Section 5.
2. EXPERIMENT
2.1. Experimental Set-Up and Conditions
The experiments were carried out at the iodine PALS. The plasma was generated with a normal incidence of the laser beam on a surface of planar solid Al or Cu targets. We have used two different harmonics of the laser radiation, the first one (1ω) with the wavelength of λ1 = 1.315 µm and the third one (3ω) with λ3 = 0.438 µm, and laser energies of 120, 290, and 580 J (in the case of the 3ω, only two first energies were available) with the pulse duration of 250 ps (full-width at half-maximum). To study the fast electron influence on the ablation pressure formation and the energy transfer to the shock wave, the experiments were carried out at small beam radii on the target surface (R L) of 40, 80, 120, and 160 µm.
These conditions of irradiation correspond to the following average values I L of the incident laser intensity on the target (averaged over the pulse duration): for E L = 120 J — from I L = 5.8 × 1014 W/cm2 (R L = 160 µm) to I L = 9.5 × 1015 W/cm2 (R L = 40 µm); for E L = 290 J — from I L = 1.4 × 1015 (R L = 160 µm) to I L = 2.3 × 1016 W/cm2 (R L = 40 µm); for E L = 580 J — from I L = 2.8 × 1015 W/cm2 (R L = 160 µm) to I L = 4.6 × 1016 W/cm2 (R L = 40 µm). The maximum achieved value of the coupling parameter Iλ2 (8.0 × 1016 Wµm2/cm2) corresponds to the energy of 580 J at 1ω and R L = 40 µm, while its minimum value (1.1 × 1014 Wµm2/cm2) corresponds to the energy of 120 J at 3ω and R L = 160 µm.
The efficiency of the plasma energy transport to the solid part of the target was determined on the basis of the crater volume measurement using the crater replica technique. Distributions of the plasma electron density at chosen times related to the laser pulse maximum were determined by three-frame interferometric system with automatic image processing. The temperatures in the near-surface plasma region were measured by means of an X-ray spectroscopy.
2.2. Interferometric and Crater Volume Measurements
The method for determination of the laser energy transferred to the shock wave by means of the crater volume measurement was proposed (Gus'kov et al., Reference Gus'kov and Gus'kov2001) and successfully employed in many experiments (Gus'kov et al., Reference Gus'kov, Borodziuk and Kalal2004; Reference Gus'kov, Kasperczuk, Pisarczyk, Borodziuk, Kalal, Limpouch, Ullschmied, Krousky, Masek, Pfeifer, Rohlena, Skala and Pisarczyk2006; Reference Gus'kov, Kasperczuk and Pisarczyk2007; Bolkhovitinov et al., Reference Bolkhovitinov, Vasin and Doskach2004). This method is based on a simple dependence of the integral degree of the target material destruction on energy losses required for the phase transition behind the front of the shock wave. In order to obtain information about the crater characteristics, the crater replicas were made of cellulose acetate. To reconstruct qualitatively the crater shape, the profiles of the crater replica in chosen cross-sections were digitized and used for calculations.
The dependencies of the crater volumes Ωcr produced in Al and Cu targets on the laser beam radii are presented in Figures 1–3 for different values of the laser energy. Figures 1 and 2 clearly demonstrate a diverse character of the dependencies found for the 1ω and 3ω, independently on the laser energy and target material. When reducing the beam radius from 160 µm to 120 µm, in the 3ω case the crater volume decreases with the decreasing R L, while in the case of the 1ω it is practically conserved. Further shortening of the R L to 40 µm does not change the degressive tendency of the crater volume in the case of the 3ω, whereas in the other case a strong growth of the crater volume is observed. These results testify that in the case of the 3ω laser radiation, the energy transferred to the solid part of the target decreases with the decreasing R L despite the increasing intensity of the laser beam. The reason for this behavior consists in lateral expansion of the laser-produced plasma accompanied by a negligible role of fast electrons in the energy transfer. By contrast, in the case of the 1ω, for which at the given intensity the parameter Iλ2 is nine times larger than that for the 3ω, the energy transferred to the solid part of the target increases with the decreasing R L, in spite of lateral expansion of the plasma plume. This energy transfer growth is particularly fast in the range of small radii (40–100 µm) providing large values of I Lλ2 and, consequently, also large energies of fast electrons.

Fig. 1. (Color online) Volumes of the craters produced in the massive Al and Cu targets versus the beam radius at the energy of 120 J for the first and third harmonics of the laser radiation.

Fig. 2. (Color online) Volumes of the craters produced in the massive Al and Cu targets versus the beam radius at the energy of 290 J for the first and third harmonics of the laser radiation.

Fig. 3. (Color online) Volumes of the craters produced in the massive Al and Cu targets versus the beam radius at the energy of 580 J for the first harmonic of the laser radiation.
The relationship between the crater volume and the laser pulse energy (intensity) Ωcr(I L) at the given R L may be approximated by an exponential function. For the largest radius (R L = 160 µm), the exponents for both harmonics vary within the range of 1.2–1.5. For the minimum radius (R L = 40 µm) and the 3ω, the exponent is close to the upper limit of this range. However, for R L = 40 µm and the 1ω, the dependence Ωcr(I L), turns out to be much stronger particularly in the 290–580 J energy range. In this case, the large values of I Lλ2 correspond to high values of the exponent equal to 3.2 and about 3 for the Al and Cu targets, respectively.
When studying the electron density distribution by three-frame interferometry, the diagnostic system used the 2ω radiation of the iodine laser. The delay between subsequent frames was set to 3 ns. For brevity, the presentation of interferometric measurements is limited to one of the energies used, namely to E L = 290 J, but analogous results were obtained for other energies. The main attention was paid to the plasma parameters just after the termination of the laser pulse, i.e., to the period when the radiation absorption is already completed. Therefore the first interferometric frame was recorded with a 2 ns delay vs. the laser beam maximum.
In Figure 4, the electron density distributions corresponding to Al (a) and Cu (b) plasmas produced by both laser harmonics at all beam radii are presented in a form of equidensitograms. In all the diagrams, the plasma expansion boundary is represented by the electron density contour n e = 1018cm−3. The step between the adjacent equidensity lines is Δn e = 2 × 1018cm−3. However, the most interesting parameter proved to be the total number of electrons in the plasma-plume (N e) computed on the basis of these diagrams. The results of interferometric and crater volume measurements for the energy of 290 J are summarized in Table 1.

Fig. 4. (Color online) Electron density distribution in Al (a) and Cu (b) plasmas measured at time of 2 ns for 1ω and 3ω laser radiation using the energy of 290 J focused to different focal spot radii.
Table 1. The results of interferometric and crater volume measurements for the energy of 290 J

Important information on features of the laser radiation absorption is provided by ratios of the total electron number to the crater volume as depicted in Figure 5. These data plotted in dependence on the focal spot radius indicate the number of electrons participating in creation of the unit crater volume (1 cm3). In the case of the 3ω, the number of electrons per unit volume is constant (Al target) or grows only slowly (Cu). It suggests that the mechanism of the laser energy transfer (or relative contributions of different mechanisms) should be the same in the whole range of R L. The values of the parameter I Lλ2 for the 3ω experiments, varying between 4.9 × 1014 and 7.8 × 1015Wμm2/cm2, are appropriate for the laser radiation absorption primarily by the inverse bremsstrahlung. For the 1ω, the situation is quite different since the number of electrons corresponding to the creation of the unit crater volume monotonically decreases with decreasing R L for both target materials. In this case the parameter I Lλ2 (varying in the range of 4.5 × 1015 −7.1 × 1016 Wμm2/cm2) is by one order of magnitude larger as compared with the 3ω irradiation at the same values of R L. For R L < 90 µm, the curves belonging to the 1ω underlay for both targets those of the 3ω. It gives the motive to suggest that besides the work of thermal electron pressure the additional mechanism of energy transfer to solid part of target occurs in the 1ω case. Since in the 1ω case the contribution of the resonant absorption of laser light enhances in comparison with the 3ω case due to significant growth the coupling parameter, it is natural to associate such an additional mechanism of energy transfer to solid target with the energy transfer by fast electrons.

Fig. 5. (Color online) The ratio of total electron number (N e) to the crater volume (Ωcr) as a function of the focal spot radius. The data were collected on massive Al and Cu targets at the laser energy of 290 J.
The numerical calculations presented below have proved that the transition from the third to the first harmonic, which corresponds to a nine-fold growth of the parameter I Lλ2, increases the energy of fast electrons even by 30% of total absorbed energy. Such transition essentially influences the ablation process and the energy transfer to the solid part of the target. Moreover, it is shown that this additional energy contribution is dominant for R L < 100 µm, when a significant part of the crater is formed via direct heating of the target by fast electrons from the hard part of its spectrum.
2.3. X-Ray Measurements
Measurements of the temperature in the near-surface plasma region were based on spectroscopic analysis of the Al K-shell self-emission. The spectra were recorded using the focusing X-ray spectrometer with the mica (002) crystal spherically bent to a radius of 150 mm. The experimental configuration was based on a classic spectroscopic scheme with the detector placed at intersection of the central ray with the Rowland circle and the source-to-crystal and crystal-to-image distances fulfilling the focusing condition in the sagittal plane (decisive for its optimum one-dimensional spatial resolution — Renner et al., Reference Renner, Uschmannand and Förster2004). This setup provides the spectral resolution comparable with the intrinsic value λ/Δλ ≈ 104 following from the dynamical theory of X-ray diffraction at bent mica crystals (Renner et al., Reference Renner, Sauvan, Dalimier, Riconda, Rosmej, Weber, Nicolai, Peyrusse, Uschmann, Höfer, Kämpfer, Lötzsch, Zastrau, Förster and Oks2008).
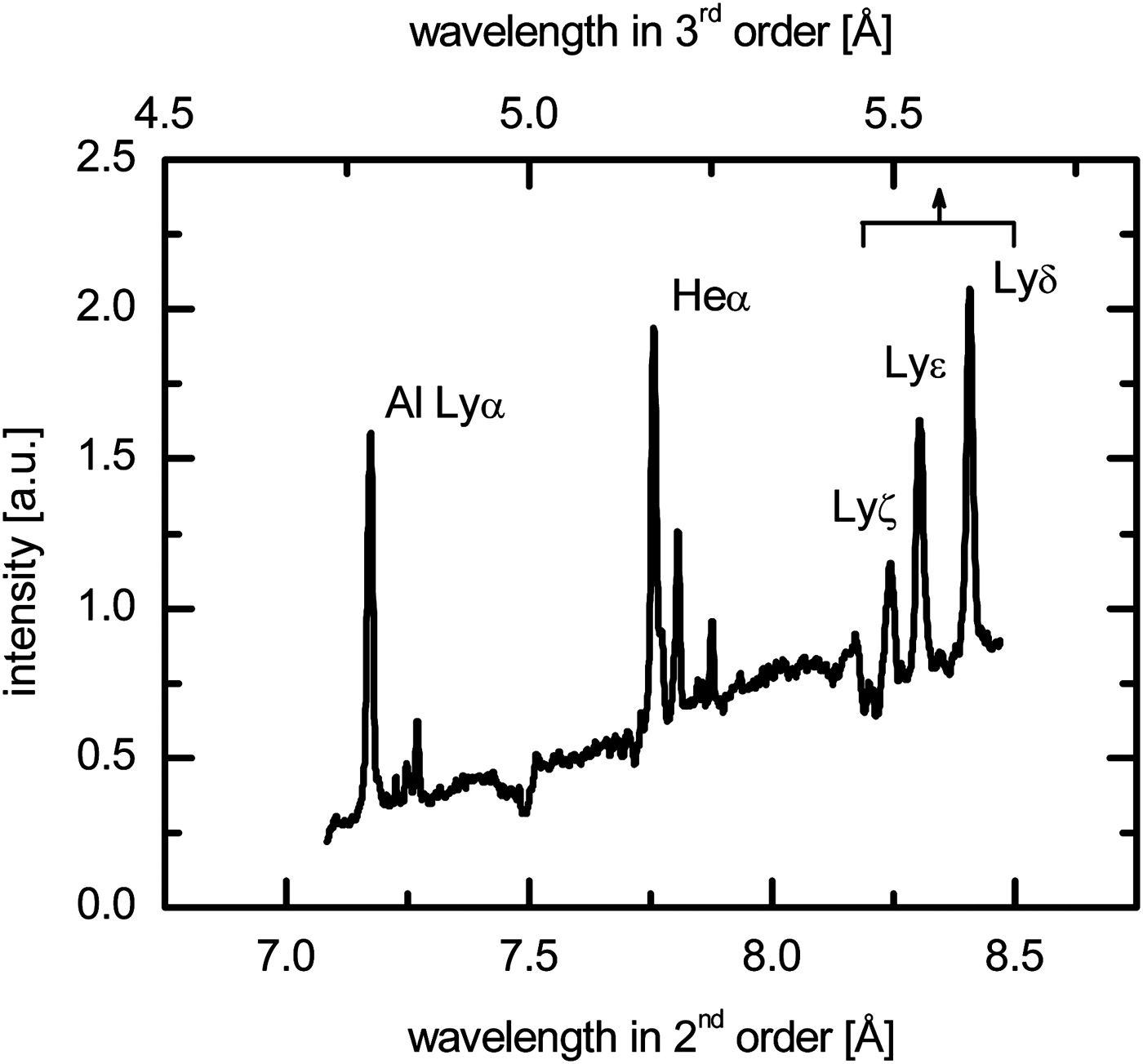
The spatially-resolved time-integrated spectra were recorded on X-ray film Kodak Industrex AA400. The spectral records were digitized and transformed to the intensity scale with respect to the wavelength-dependent crystal reflectivity, transmission of the filters used and the film response. An example of the recorded spectrum is shown in Figure 6. This spectral lineout corresponds to the plasma emission observed in a distance of 50 µm from the target surface when irradiating the massive Al by the 1ω laser focused to R L = 160 μm (intensity of 4.8 × 1015 W/cm2). The spectrum recorded in the second spectroscopic order consists of the resonance L yα line emission (2p 2P3/2,1/2 → 1s 2S1/2) of the hydrogenic Al, the resonance w (1s2p 1P1 → 1s 21S0) and intercombination y (1s2p 3P1 → 1s 21S0) lines in the He-α group and their satellites. The higher members δ−ζ of the Lyman spectroscopic series (np 2P → 1s 2S1/2) were recorded in the third spectroscopic order and their widths provided the diagnostically important information about the plasma density. The effective plasma parameters (i.e., those corresponding to the plasma conditions in the period of the strong X-ray emission — Renner et al., Reference Renner, Sondhauss, Peyrusse, Krouský, Ramis, Eidmann and Förster1999) were determined from the best fit of the experimentally observed and synthetic spectral profiles simulated by the PrismSPECT code (MacFarlane et al., Reference MacFarlane, Golovkin, Wang, Woodruff and Pereyra2007) under assumption of the homogeneous plasma slab and the steady-state approximation. The details of the fitting procedure can be found in the paper (Smid et al., Reference Šmíd, Antonelli and Renner2013).

Fig. 6. K-shell plasma emission from the massive Al target irradiated by the first harmonic of the laser radiation focused to R L = 160 µm.
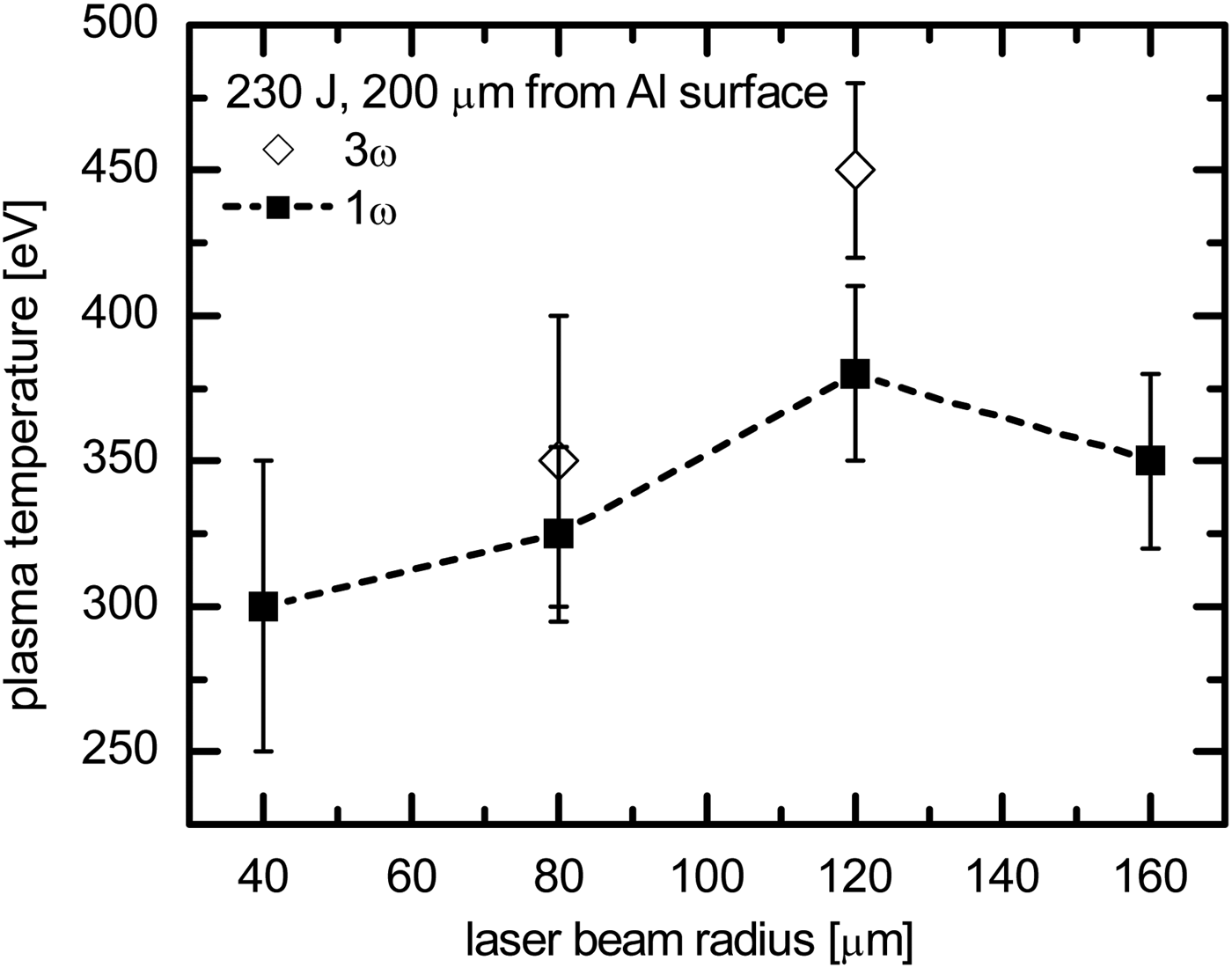
The plasma temperatures measured on massive Al targets irradiated by 230 J of the 1ω and 3ω laser radiation at different focal radii are presented in Figure 7. They characterize the plasma regions in the distance of 200 µm from the original surface of the targets. A remarkable feature of this data consists in a non-monotonic behavior of the temperature in dependence on the radius of the focused 1ω laser beam. For larger focal spots, the plasma temperature grows with the decreasing radii and, vice versa, the temperature drops down along with the radii in the range of their smaller values. The two open points related to the third laser harmonics indicate that the temperature of the plasma produced by the 3ω beam is by a factor of 1.2–1.3 higher than that created by the 1ω beam.

Fig. 7. Plasma temperatures spectroscopically measured at the distance of 200 µm above the surface of the massive Al target irradiated at different laser harmonics and focal radii at the laser energy of 230 J.
3. NUMERICAL SIMULATIONS
The numerical simulations of the laser beam interaction with the Al massive target were carried out using the 2D hydrodynamic code ATLANT-HE (Lebo et al., Reference Lebo, Demchenko, Iskakov, Limpouch, Rozanov and Tishkin2004). This code includes refraction of the laser radiation in the plasma, inverse bremsstrahlung and resonance mechanisms of the laser radiation absorption, generation of fast electrons due to the resonance absorption, and the fast electron energy transfer with Coulomb collisions taken into account. Computations were performed for the Al target and two values of the beam radius, 40 and 120 µm. In the code, the cylindrical coordinates (r, z) were applied assuming an axial symmetry of both the laser beam and the plasma. The size of plasma non-homogeneities in the vicinity of critical plasma density was computed by using an analytical model including ponderomotric force (Gus'kov et al., Reference Gus'kov, Demchenko, Makarov, Rozanov, Satov and Sharkov2011). This model describes a dissipative structure of the plasma flow in the plasma region with the critical density, in contrast to a dispersive structure described by the Korteveg-de-Vries equation.
In the case of the dispersive structure, the scale of the plasma inhomogeneities is of an order of Debye length. The dissipative structure gives much larger scale of the plasma inhomogeneities comparable with the wavelength of the laser radiation. Meanwhile, contribution of the resonance absorption and consequently, also the fast electron energy depend on the scale of the plasma inhomogeneities (Gus'kov et al., Reference Gus'kov, Demchenko, Makarov, Rozanov, Satov and Sharkov2011). In numerical calculations, the fast electrons are accelerated near the critical surface by a longitudinal field directed normally to that surface, i.e., an initial direction of the fast electron motion coincides with the normal to the critical surface. On the plasma-vacuum boundary, a mirror reflection of the fast electrons occurs as the electrons escaping beyond the plasma border are turned back to the plasma by the electric field of the charge separation.
At the beginning, let us discuss the results of calculations referring to the absorption of the laser radiation and a state of the laser-produced plasma for conditions of the considered experiments. Table 2 presents the total fraction δa of the laser energy absorbed by both inverse bremsstrahlung and resonance mechanisms, and the fraction δra of the laser energy absorbed by resonance mechanism only. Almost the whole energy absorbed by the resonance mechanism is transported by a flow of fast electrons.
Table 2. Comparison the crater volume measurements and the numerical simulations regarding the total fraction of the laser energy absorbed by both inverse bremsstrahlung δa and resonance mechanisms δra

Contribution of the resonance absorption depends on incidence angles of the laser rays, i.e., on their deviation from the optimum angle. This optimum angle corresponds to the value of parameter τ = (k 0L)1/3sinθ0 = 0.7 (Ginzburg, Reference Ginzburg1970), where k 0 is a wave number of the laser radiation, L is a size of the plasma inhomogeneities toward the density gradient, and θ0 is the angle of incidence. During the 2D plasma expansion, the incidence angle is determined by a value of dielectric permeability at the point of the beam reflection (r*,z*): sinθ0 = [ε(r*,z*)]1/2. When the incidence angle differs from the optimum one, the efficiency of the resonance absorption decreases. If the radiation is fully p-polarized and if it strikes the target at the optimum angle, the resonance absorption efficiency is on the level of 50% (Freidberg, Reference Freidberg, Mitchell, Morze and Rudsinski1972). The calculations assume a Gaussian laser beam impacting the target surface in the characteristic focal spot radius R L. The angle of the beam incidence for r = R L equals 13°. In the case of axially symmetric irradiation, only a half of the laser beam is p-polarized, whereas the second half impinges with s-polarization. Even if all rays of the laser beam strike the target at the optimum angle, the resonance absorption efficiency cannot be larger than 25%. As the rays are incident at different angles, the total efficiency of the resonance absorption is significantly lower than 25% (see Table 2). The computations manifested univocally that the efficiency of the inverse bremsstrahlung absorption for the 3ω is much higher than that for the 1ω (see Table 2). This results from higher density of the subcritical plasma in the 3ω case. For the 1ω, the contribution of the resonance absorption at R L = 120 µm is slightly higher than that at R L = 40 µm. A wider focal spot is accompanied by a larger transverse dimension of the plasma, thus the inclination of the density gradient from the z-axis is smaller and the angles between individual rays and the density gradient vector prove to be closer to the optimum value.
This is clearly seen in Figure 8, where the density distribution in the plasma plumes at the time of 0.2 ns (corresponding to the maximum intensity of the laser beam) for the 1ω and R L = 40 and 120 µm are presented. The equidensity line number 5 represents the critical surface (ρcr = 2.72 × 10−3g/cm3), the vector of the density gradient is normal to it. This figure confirms that the wider focal spot results in the smaller angle between the density gradient on the critical surface and the z-axis. In the 3ω case, the contribution of the resonance absorption turns out to be smaller for a wider beam spot than for a narrower one. This is caused by the high efficiency of the inverse-bremsstrahlung absorption for the 3ω beam. The efficiency increases for wider focal spots since the plasma density and temperature decrease with the increasing beam radius. In addition, the laser radiation reaching the critical surface at the optimum angle of incidence is considerably attenuated and the contribution of the resonance absorption decreases. The computed values of the total absorption δa integrated over all rays can be found in Table 2. We point out that the rays with the optimum participation in the resonance absorption are characterized by a higher efficiency of the inverse-bremsstrahlung absorption. As demonstrated by numerical simulations, in the 3ω case the critical surface is located closer to the target surface than in the 1ω case. Consequently at R L = 40 µm, the angles of incidence for the 3ω are closer to the optimum value than those for the 1ω and the contribution of the resonance absorption is larger for the 3ω beam (see Table 2).

Fig. 8. (Color online) Density distribution inside the plasma plume for the massive Al target irradiated by the 1ω laser pulse: (a) at the focal spot radius of 40 µm and (b) 120 µm.
Figure 9 presents the distributions of the mass density and electron and ion temperatures in the plasma plume generated on the Al target by an action of the 1ω laser radiation. We note that this is the most interesting case from the point of view of the influence of fast electrons. The maximum electron temperature values of 3 keV for R L = 40 µm (the point with the coordinate z = 1693 µm in the left diagram) and 2.5 keV for R L = 120 µm (z = 1680 µm in the right diagram) differ only slightly one from another. The expected growth of the temperature at smaller R L resulting from the increased radiation intensity is compensated by the amplified effect of the lateral plasma plume expansion. However, in the vicinity of the ablation surface (i.e., near z = 1680 µm) the temperatures of 0.4 and 0.6 keV for the radii of 40 µm and 120 µm, respectively, are in an opposite relation. It should be pointed out that the density near the ablation surface, which can be associated with ablation density, 0.28 g/cm3 for R L = 40 µm exceeds a value of 0.17 g/cm3 for R L = 120 µm. Simultaneously, the calculations proved that in the 3ω case, which corresponds to the fast electrons absence, the ablation density decreases with the decreasing beam radius due to the lateral expansion of the plasma plume. The maximum temperature values in the 3ω case are 4 keV for R L = 40 µm and 3 keV for R L = 120 µm, i.e., higher than those for the 1ω case. This is in agreement with the theoretically predicted higher value of the laser absorption efficiency.

Fig. 9. (Color online) Distribution of the mass density, electron and ion temperature on the axis of plasma plume for the massive Al target irradiated by the 1ω laser pulse: (a) using the focal spot radius of 40 µm and (b) 120 µm.
To calculate the crater volume which constitutes a criterion for evaporation of the target material, its heating to the temperature T * = 2.2T cr (Zel'dovich, Reference Zel'dovich and Raizer2002) (where T cr is the critical temperature in the Van der Waals state equation) was taken into account. Despite this sample evaporation criterion was considered for lead (Grigor'ev & Meilikhov, Reference Grigor'ev and Meilikhov1991), hitherto there is no accurate theoretical formulation of this criterion. The criterion T * = 2.2T cr assumes that the material is ejected from the crater as a gas which does not condense over a period considered. However, the material can also be ejected from the crater as a mixture of the gas and liquid droplets assuming that a partial condensation of vapor occurs in the ejected material. Therefore a more appropriate evaporation criterion should rather be deduced empirically.
In our calculations, the front surface z f (r) with the temperature value of T * was determined. It was assumed that the target material is heated both due to the shock wave expansion and the fast-electron energy transfer. The calculations permitted only increasing values of the coordinate z f (r). If the z f (r) value changed its sign during the calculation, the last (maximum) value of z f (r) was taken into account. In this way, the crater contour and volume 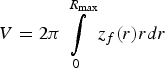 $V = 2{\rm \pi} \vint\limits_0^{R_{\max }} z_f \lpar r\rpar rdr$ were obtained. The critical surface is not planar, it can be qualitatively approximated by a spherical cap. Fast electrons are characterized by a sufficiently wide range of motion vectors with respect to the optical axis, this divergence further grows due to their reflection from the plasma border. Thereby the surface of the crater produced by fast electrons has a quasi-spherical shape. The surface of the crater created by the shock wave should also be spherical, because the size of the area of the laser energy absorption is small in comparison with the crater dimension and thus the shock wave turns out to be almost spherical.
$V = 2{\rm \pi} \vint\limits_0^{R_{\max }} z_f \lpar r\rpar rdr$ were obtained. The critical surface is not planar, it can be qualitatively approximated by a spherical cap. Fast electrons are characterized by a sufficiently wide range of motion vectors with respect to the optical axis, this divergence further grows due to their reflection from the plasma border. Thereby the surface of the crater produced by fast electrons has a quasi-spherical shape. The surface of the crater created by the shock wave should also be spherical, because the size of the area of the laser energy absorption is small in comparison with the crater dimension and thus the shock wave turns out to be almost spherical.
As mentioned earlier, the calculations were carried out for the Al target with the laser energy of 290 J, which corresponds to the experimental results presented in Figure 2. The value of T cr for Al was assumed to be equal to 0.32 eV (Grigor'ev & Meilikhov, Reference Grigor'ev and Meilikhov1991). In Grigor'ev and Meilikhov, the value of T cr is not given, for most of analogous materials T cr ≈ 4T m, where T m is a melting temperature. According to this estimation, the value T* = 2.2T cr = 0.7 eV was chosen for Al. The calculations performed for two beam radii (40 and 120 µm) and two laser wavelengths indicate that for R L = 40 µm and the 1ω radiation, the crater volume is limited by a depth of the target overheating by fast electrons. In three alternate calculations (R L = 40 for the 3ω, and R L = 40 and 120 µm for both harmonics) the crater volumes are limited by the shock wave damping depths. It should be noted that the heating by fast electrons, whose energy is fully transformed into the internal energy of the target material, is more effective than the heating by the shock wave. Behind the shock wave front only a part (although big) of the energy is deposited into the internal energy of the material, while the rest is deposited into the kinetic energy (in the case of a strong shock wave, these energies are equal to each other). Besides, the internal energy is divided into elastic (cold) and thermal energy. For the 1ω, both these components contribute to the ratio of the crater volumes for R L = 40 µm and 120 µm (which is close to four, according to the experimental data in Table 2). The calculations show that for the temperature of 0.7 eV behind the shock wave front, the thermal and cold components of the internal energy are almost equal.
The experimental and computational values of the crater volumes are given in Table 2. In the 1ω case, both computational and experimental data demonstrate the increase of the crater volume with the decreasing beam radius. This is a direct consequence of the growing depth of the target overheating by fast electrons, the average energy of which increases with the growing laser intensity. In the case of R L = 40 µm and the 1ω irradiation, the calculated free path lengths of fast electrons and the crater dimensions match perfectly up. At a nine-fold reduction of the laser beam intensity for R L = 120 µm, the fast electron energy decreases approximately only twice. Their range decreases roughly with the energy square and becomes much smaller than the crater size. At 3ω, the fast electron energy decreases approximately proportionally to the ratio of the squares of laser radiation frequencies, i.e., also by a factor of 9. In this case, the material is vaporized from the crater due to its heating by the shock wave. The decrease of the crater volume with the decreasing R L is connected with a more pronounced role of the lateral expansion of the plasma plume.
Let us now evaluate the maximal energy and the fast electron free path for the case of R L = 40 µm and the 1ω. The maximal energy, approximately equal to double oscillation energy (2E os) of the resonance field on the critical surface, is gained by fast electrons moving towards the plasma plume border. After reflection from the border, they come back to the target, passing twice through the plasma resonance area. The other part of electrons, which propagate toward the solid target and pass only once through the plasma resonance point has the energy of an order of E os. To estimate the resonance field, the following formula was employed (Gus'kov et al., Reference Gus'kov, Demchenko, Makarov, Rozanov, Satov and Sharkov2011).
where |H 0| is the field amplitude of the incident wave, Φ(τ) is the resonance function (Ginzburg, Reference Ginzburg1970) (the maximum value of this function equals to 1.2 for τ = 0.7), ε2 = (βT / k 0L)2/3, βT = (T e / m ec 2)1/2. From the calculations, the values of T e = 3 keV (at the time of 0.2 ns) and k 0L = 6.3 were obtained. By using the value of |H 0| = 1.39 × 107 (in CGS units), the oscillation energy value equals to E os = e 2|E c|2/2m eω2 = 97 keV. Hence the maximum energy of fast electrons is 2E os = 194 keV due to its double passing through the resonance area.
The non-relativistic fast electron free path length at ionization of the cold material is (Berestetskii et al., Reference Berestetskii, Lifshitz and Pitaevskii1982; Landau & Lifshitz, Reference Landau and Lifshitz1965)
where E 0 is the initial energy of fast electrons, Z and m i — charge and mass of nucleus, ρ0 — material density. Λ* represents the Coulomb logarithm
where I is an average ionization potential (in the atom model by Thomas-Fermi I ≈ 14.9 ZeV) and e n — the Euler number. Experimental value of crater volume (and closed numerically calculated value) of 4 × 10−3cm3 for beam radius of 40 μm corresponds to the crater radius equal to R cr = 5.8 × 10−2 cm (suggesting a crater as semi-sphere with a volume (2π/3)R cr3). By using Eqs. (2) and (3) for the case of R L = 40 µm (when E 0 = 194 keV), the free path length L at Λ* = 3.2 is equal to R cr. Thus, in this case, the crater formation can be explained by direct material heating by fast electrons. It should be pointed out that the above estimated sufficient values of the fast electrons energy and their free path length in the target material are connected with an increase of the longitudinal field in the vicinity of the critical surface for the p-polarized laser radiation. Such field rise is absent in the case of s–polarization (Wilks et al., 1982).
As seen in Table 2, the most adequate numerical reconstruction of the crater volume corresponds to the case of the target heating by fast electrons at R L = 40 µm and 1ω. In other cases where the target heating is realized by the shock wave, the dependence of the crater volume on R L and the laser frequency has only a qualitative character. It can be explained by the application of the approximate equation of state, which is reasonably accurate only at low pressures and temperatures when the shock wave becomes almost an acoustic wave. At temperatures near and above T cr, the accuracy of this equation decreases. One of the most important future studies applicable to the crater creation in solid materials by the shock wave seems to be the formulation of more accurate equations of state in the range of temperatures and pressures comparable with the Van-der Vaals critical values.
4. GENERALIZED THEORETICAL MODEL AND DISCUSSION OF THE RESULTS
Three effects determine the laser-produced plasma state and ablation pressure value in the discussed experiments with the tightly focused laser beam at intensities larger than 1015 W/cm2, namely, electron thermal conductivity, fast-electron energy transport, and lateral plasma expansion. Therefore the analytical model of axially symmetric lateral plasma expansion due to the pulse ablation proposed (Gus'kov et al., Reference Gus'kov, Borodziuk and Kalal2004) was developed here. The model is based on an application of self-similar solution (Imshennik, Reference Imshennik1960), describing the isothermal expansion of a portion of the material with a given mass, where the density ρ, temperature T, and velocity u of the expanding material have forms
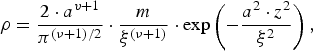 $${\rm \rho} = \displaystyle{2 \cdot a^{v + 1} \over {\rm \pi}^{\lpar {\rm \nu} + 1\rpar /2}} \cdot \displaystyle{m \over {\rm \xi}^{\lpar {\rm \nu} + 1\rpar}} \cdot \exp \left( - \displaystyle{a^2 \cdot z^2 \over {\rm \xi}^2} \right)\comma \;$$
$${\rm \rho} = \displaystyle{2 \cdot a^{v + 1} \over {\rm \pi}^{\lpar {\rm \nu} + 1\rpar /2}} \cdot \displaystyle{m \over {\rm \xi}^{\lpar {\rm \nu} + 1\rpar}} \cdot \exp \left( - \displaystyle{a^2 \cdot z^2 \over {\rm \xi}^2} \right)\comma \;$$In this case, the pressure P and the sound velocity V s are defined by relations
where ν = 0,1, and 2 correspond to the plane, cylindrical and spherical geometries of the expansion, z and t are the current coordinate and time, ξ is a coordinate of the plasma plume front (this is the length of the plume in the plane expansion or the plume radius in the spherical one):
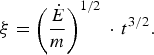 $${\rm \xi} = \left({\dot{E} \over m}\right)^{1/2}\, \cdot \,t^{3/2}.$$
$${\rm \xi} = \left({\dot{E} \over m}\right)^{1/2}\, \cdot \,t^{3/2}.$$
In the case of the plane expansion, ![]() $\,\dot{\!E} \equiv I_a$ is the rate of the energy delivery per unit area, i.e., the intensity of the absorbed laser radiation, and m ≡ ms is the mass of the expanding material per unit surface area (the areal mass). For the spherical expansion,
$\,\dot{\!E} \equiv I_a$ is the rate of the energy delivery per unit area, i.e., the intensity of the absorbed laser radiation, and m ≡ ms is the mass of the expanding material per unit surface area (the areal mass). For the spherical expansion, ![]() $\,\dot{\!E} \equiv I_a \cdot {\rm \pi} \cdot R_L^2$ is the total rate of the energy delivery or the absorbed radiation power, I a = a · I L and m ≡ m t is the total mass of the expanding material. The specific heat C ν is defined by relation C ν = (Z + 1)k/A(γa − 1)m p, where A and Z are the atomic weight of the plasma ions and an average degree of the plasma ionization, m p is the proton mass, k is the Boltzmann constant; γ is the adiabatic index, and the constant a is given by
$\,\dot{\!E} \equiv I_a \cdot {\rm \pi} \cdot R_L^2$ is the total rate of the energy delivery or the absorbed radiation power, I a = a · I L and m ≡ m t is the total mass of the expanding material. The specific heat C ν is defined by relation C ν = (Z + 1)k/A(γa − 1)m p, where A and Z are the atomic weight of the plasma ions and an average degree of the plasma ionization, m p is the proton mass, k is the Boltzmann constant; γ is the adiabatic index, and the constant a is given by
 $$a = \left[3 \cdot {3{\rm \gamma} \cdot \lpar {\rm \nu} + 1\rpar - \lpar 3{\rm \nu} + 1\rpar \over 16 \cdot \lpar {\rm \gamma} - 1\rpar } \right]^{1/2}.$$
$$a = \left[3 \cdot {3{\rm \gamma} \cdot \lpar {\rm \nu} + 1\rpar - \lpar 3{\rm \nu} + 1\rpar \over 16 \cdot \lpar {\rm \gamma} - 1\rpar } \right]^{1/2}.$$A proposed approach to the construction of the lateral expansion model for the laser beam interaction with the planar target (Gus'kov et al., Reference Gus'kov, Borodziuk and Kalal2004) consists in a combination of Eqs. (4)–(9) for the plane (ν = 0) and spherical (ν = 2) geometries in one solution, being a function of the parameter ξ/R L. In Gus'kov et al. (Reference Gus'kov, Borodziuk and Kalal2004), such model was constructed for two variants of the mass source, namely, (1) for the mass source determined by the steady-state hydrodynamic ablation due to the inverse bremsstrahlung absorption of the laser radiation in the plasma region with the critical density, and (2) for the mass source induced by the ablation due to the heating by mono energetic fast electrons with the energy equal to the laser energy absorbed by the resonance mechanism.
It should be noted that in the case of the planar geometry, solution (4)–(9) corresponds exactly to the mass source induced by the fast electrons, because the fast-electron stopping range does not depend on the plasma temperature being determined only by the initial electron energy. In other cases, such as the hydrodynamic ablation considered (Gus'kov et al., Reference Gus'kov, Borodziuk and Kalal2004) and the thermal conductivity ablation discussed below, the mass of the vaporized material increases with time. Therefore, the self-similar solution to be employed under the mass change conditions using an average mass value over the considered period was proposed (Gus'kov et al., Reference Gus'kov, Borodziuk and Kalal2004). At this assumption, the mass of the vaporized material in the case of the hydrodynamic ablation is determined by the formula (Gus'kov et al., Reference Gus'kov, Borodziuk and Kalal2004)
where the critical density has the form
Using Eq. (12) and Eqs. (4)–(9) and assuming γ = 5/3 for the high-temperature plasma, we obtain
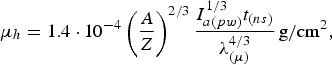 $${\rm \mu}_h = 1.4 \cdot 10^{-4} \left({A \over Z} \right)^{2/3} {I_{a\lpar pw\rpar }^{1/3} t_{\lpar ns\rpar } \over {\rm \lambda}_{\lpar {\rm \mu}\rpar }^{4/3}}\, \hbox{g}/\hbox{cm}^2\comma \;$$
$${\rm \mu}_h = 1.4 \cdot 10^{-4} \left({A \over Z} \right)^{2/3} {I_{a\lpar pw\rpar }^{1/3} t_{\lpar ns\rpar } \over {\rm \lambda}_{\lpar {\rm \mu}\rpar }^{4/3}}\, \hbox{g}/\hbox{cm}^2\comma \;$$where I a(pw) and λ(μ) are measured in PW/cm2 and μm, respectively.
The mass of the material vaporized due to the heating by fast electrons is defined by their stopping range. The stopping range of non-relativistic fast electrons with the energy E 0 in totally ionized plasma under the approximation of the absent scattering equals to (see e.g., Gus'kov et al., Reference Gus'kov, Ribeyre and Touati2012; Atzeni et al., Reference Atzeni, Schiavi, Honrubia, Ribeyre, Schurtz, Nicolai, Olazabal-Loumé, Bellei, Evans and Davies2008)
where E 0(keV) is the initial energy of fast electrons in keV and Λ = 5.
It is convenient to use an analytical scaling for the dependence of the average fast electron energy on the coupling parameter I Lλ2 that, according to the data of the above discussed numerical simulations, could be proposed as
where I L(pw) is the intensity of laser radiation in PW/cm2. Substituting this expression into Eq. (14), we get for the area mass of the material vaporized by fast electron heating
The area mass vaporized by the thermal conductivity wave is determined by the standard equation
where f is the limitation factor and κ may be expressed for the Coulomb logarithm equal to 5 as
Assuming ∂T/∂x ≈ 5T/3x and using Eq. (5) for the temperature, we obtain the following result for the average value of areal mass:
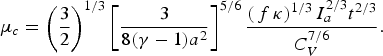 $${\rm \mu}_c = \left(\displaystyle{3 \over 2} \right)^{1/3} \left[\displaystyle{3 \over 8\lpar {\rm \gamma} - 1\rpar a^2} \right]^{5/6} \displaystyle{\left(\,f\,{\rm \kappa} \right)^{1/3} I_a^{2/3} t^{2/3} \over C_V^{7/6}}.$$
$${\rm \mu}_c = \left(\displaystyle{3 \over 2} \right)^{1/3} \left[\displaystyle{3 \over 8\lpar {\rm \gamma} - 1\rpar a^2} \right]^{5/6} \displaystyle{\left(\,f\,{\rm \kappa} \right)^{1/3} I_a^{2/3} t^{2/3} \over C_V^{7/6}}.$$By substituting the values of a at ν = 0 (see Eq. (10)), κ and C V into expression (19), then assuming γ = 5/3, we get
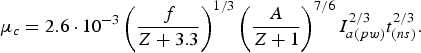 $${\rm \mu}_c = 2.6 \cdot 10^{ - 3} \left(\displaystyle{\,f \over Z + 3.3} \right)^{1/3} \left(\displaystyle{A \over Z + 1} \right)^{7/6} I_{a\lpar pw\rpar }^{2/3} t_{\lpar ns\rpar }^{2/3}.$$
$${\rm \mu}_c = 2.6 \cdot 10^{ - 3} \left(\displaystyle{\,f \over Z + 3.3} \right)^{1/3} \left(\displaystyle{A \over Z + 1} \right)^{7/6} I_{a\lpar pw\rpar }^{2/3} t_{\lpar ns\rpar }^{2/3}.$$For all three ablation mechanisms, the vaporized mass increases with the increasing laser intensity, however the fastest growth concerns the heating by fast electrons, whereas the slowest one relates to the hydrodynamic ablation. The mass vaporized by the thermal conductivity wave does not depend on the laser wavelength, in contrast to two other ablation mechanisms. For the hydrodynamic ablation, the mass decreases as λ−4/3, while for the fast electron ablation it grows as λ8/3. The mass vaporized by the fast electron heating does not depend on the laser pulse duration, whereas in the case of alternate ablation mechanisms this mass increases with the increasing laser pulse duration.
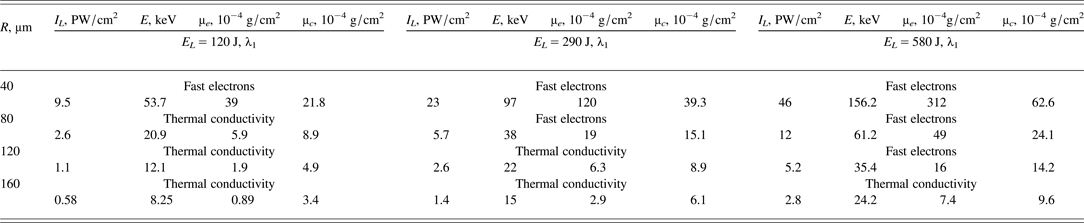
In this Section, the generalized model is used for detailed interpretation of experiments with Al targets and for qualitative comparative analysis of the Al and Cu targets behavior. In calculations, the following values of different quantities were used: A = 27, Z = 11, t = 0.25 ns, δa = 0.32 for the 1ω and δa = 0.8 for the 3ω (the average values of the absorption coefficient correspond to the numerical simulation, see Table 2). The calculations show that in all of the analyzed experiments with a relatively short (0.25 ns) laser pulse irradiation and at energies varying from 100 to 600 J, the role of “thermal” ablation induced by the electron conductivity considerably exceeds the role of the hydrodynamic ablation for both laser harmonics. For the 3ω, the target ablation is determined by the electron conductivity for all values of the energy and the focal spot radius used. A more complex situation occurs for 1ω, the state of the plasma plume is determined by a competition between the energy transfer processes due to thermal conductivity and fast electrons. The values of the area vaporized mass of the Al target calculated on the basis of (13), (16), and (20) for the 1ω irradiation are collected in Table 3, where the dominant ablation mechanisms are indicated.
Table 3. The values of the area vaporized mass of the Al target calculated on the basis of the analytical model [Gus'kov et al., Reference Gus'kov, Borodziuk and Kalal2004] for the 1w irradiation and different energy in the case of the different the ablation mechanisms

For all energies and the beam radius of 160 µm, the mass vaporized due to the thermal conductivity exceeds that due to the fast electron transport. However, increasing the contribution of fast electrons in the ablation process with the rise of the laser intensity (due to decreasing R L) leads to a situation that at R L = 40 µm for all energies the mass vaporized by the fast electron heating exceeds that resulting from the propagation of thermal conductivity wave. Note that for the energy of 580 J this inversion takes place for R L = 120 µm. Therefore, two types of the mass source should be applied.
The first one driven by the thermal conductivity is adequate for the 3ω irradiation in the whole ranges of energies and beam radii used and for the 1ω irradiation with the energy of 120 J and laser beam radii R L = 160, 120, and 80 µm, with the energy of 290 J and R L = 160 and 120 µm, and with the energy of 580 J and R L = 160 µm. The other one driven by the fast electron heating is adequate in the case of the 1ω for the energy of 120 J and radius R L = 40 µm, for the energy of 290 J and R L = 40 and 80 µm, and for the energy of 580 J and R L from 120 to 40 µm.
Under conditions of a few competing ablation mechanisms, the model of the laser-produced plasma using Eqs. (4)–(9) is created in the following way. The mass of the plasma plume is assumed to be the largest part of the vaporized mass corresponding to the dominant mechanism of ablation and the total absorbed energy is deposited in this mass. Then the characteristic size of the plasma plume determined by the expansion velocity of the vaporized material can be calculated using the Eq. (9), where the total intensity of the absorbed laser radiation and the higher of the two area masses μc and μe are substituted:
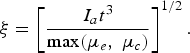 $${\rm \xi} = \left[\displaystyle{I_a t^3 \over \max \lpar {\rm \mu}_e\comma \; {\rm \mu}_c \rpar} \right]^{1/2}.$$
$${\rm \xi} = \left[\displaystyle{I_a t^3 \over \max \lpar {\rm \mu}_e\comma \; {\rm \mu}_c \rpar} \right]^{1/2}.$$Inserting the value of μc or μe in Eq. (21), then according to Eqs. (16) and (20) the following expressions for the ratio of the plasma plume dimension to the focal beam radius for both above mentioned ablative mechanisms are obtained
 $$\displaystyle{{\rm \xi}_c \over R_L} = 5.1 \cdot 10^{- 3} \left(\displaystyle{Z + 3.3 \over f} \right)^{1/6} \left(\displaystyle{Z + 1 \over A} \right)^{7/12} \displaystyle{E_{a\lpar J\rpar}^{1/6} t_{\lpar ns\rpar} \over R_{L\lpar cm\rpar}^{4/3}}\comma \;$$
$$\displaystyle{{\rm \xi}_c \over R_L} = 5.1 \cdot 10^{- 3} \left(\displaystyle{Z + 3.3 \over f} \right)^{1/6} \left(\displaystyle{Z + 1 \over A} \right)^{7/12} \displaystyle{E_{a\lpar J\rpar}^{1/6} t_{\lpar ns\rpar} \over R_{L\lpar cm\rpar}^{4/3}}\comma \;$$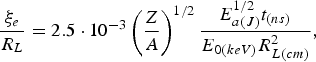 $$\displaystyle{{\rm \xi}_e \over R_L} = 2.5 \cdot 10^{-3} \left(\displaystyle{Z \over A} \right)^{1/2} \displaystyle{E_{a\lpar J\rpar }^{1/2} t_{\lpar ns\rpar} \over E_{0\lpar keV\rpar} R_{L\lpar cm\rpar}^2}\comma \;$$
$$\displaystyle{{\rm \xi}_e \over R_L} = 2.5 \cdot 10^{-3} \left(\displaystyle{Z \over A} \right)^{1/2} \displaystyle{E_{a\lpar J\rpar }^{1/2} t_{\lpar ns\rpar} \over E_{0\lpar keV\rpar} R_{L\lpar cm\rpar}^2}\comma \;$$where E a(J) is the absorbed laser energy (in J). Applying the scaling (15) for the fast electron energy, Eq. (23) takes a form
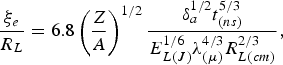 $$\displaystyle{{\rm \xi}_e \over R_L} = 6.8\left(\displaystyle{Z \over A} \right)^{1/2} \displaystyle{{\rm \delta}_a^{1/2} t_{\lpar ns\rpar}^{5/3} \over E_{L\lpar J\rpar}^{1/6} {\rm \lambda}_{\lpar {\rm \mu} \rpar}^{4/3} R_{L\lpar cm\rpar}^{2/3}}\comma \;$$
$$\displaystyle{{\rm \xi}_e \over R_L} = 6.8\left(\displaystyle{Z \over A} \right)^{1/2} \displaystyle{{\rm \delta}_a^{1/2} t_{\lpar ns\rpar}^{5/3} \over E_{L\lpar J\rpar}^{1/6} {\rm \lambda}_{\lpar {\rm \mu} \rpar}^{4/3} R_{L\lpar cm\rpar}^{2/3}}\comma \;$$where E L(J) is the laser energy (in J). For constant laser energy, the ratio ξ/R L, which characterizes the degree of 2D expansion, increases with the decreasing beam radius as R L−4/3 in the case of ablation caused by the electron conductivity and as R L−2/3 in the case of ablation due to the fast electron heating. Calculations of the ratio ξ/R L by means of (22) and (24) for the 1ω and 3ω assuming the total absorption coefficient δa, equal to 0.32 and 0.8, respectively, show that the lateral expansion of the plasma plume plays a relevant role in experiments with the tightly focused beam. Connected with this, the decrease of the ablation pressure seems to be one of the most important components of the model describing the laser-produced plasma state. In particular, the lateral expansion turns out to be important for the focal beam radii smaller than R L = 120 µm. When the focal beam radius is reduced to 100–120 µm, the ratio ξ/R L increases above 1 and reaches the values exceeding 2 for R L = 40 µm in the case of the 1ω and 4 in the case of the 3ω, respectively.
According to (Gus'kov et al., Reference Gus'kov, Borodziuk and Kalal2004), the expressions for the laser-produced plasma temperature and density on the ablation border (x = 0) can be written in the form of superposition of self-similar solutions (4)–(9) for the planar (ν = 0) and spherical (ν = 2) geometries of expansion by using the parameter ξ/R L as follows (γ = 5/3):
where T 0 and ρ0 are the temperature and density of the self-similar solution for planar expansion
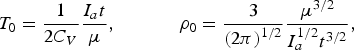 $$T_0 = \displaystyle{1 \over 2C_V} \displaystyle{I_a t \over {\rm \mu}}\comma \; \quad \quad \quad {\rm \rho}_0 = \displaystyle{3 \over \left(2{\rm \pi} \right)^{1/2}}\displaystyle{{\rm \mu}^{3/2} \over I_a^{1/2} t^{3/2}}\comma \;$$
$$T_0 = \displaystyle{1 \over 2C_V} \displaystyle{I_a t \over {\rm \mu}}\comma \; \quad \quad \quad {\rm \rho}_0 = \displaystyle{3 \over \left(2{\rm \pi} \right)^{1/2}}\displaystyle{{\rm \mu}^{3/2} \over I_a^{1/2} t^{3/2}}\comma \;$$and Ψ is the factor of temperature and density decrease at the transition to spherical expansion:
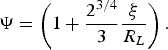 $$\Psi = \left(1 + \displaystyle{2^{3/4} \over 3} \displaystyle{{\rm \xi} \over R_L} \right).$$
$$\Psi = \left(1 + \displaystyle{2^{3/4} \over 3} \displaystyle{{\rm \xi} \over R_L} \right).$$For the large values of ξ/R L, solution (25)–(26) converts in the self-similar solution for spherical expansion
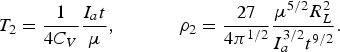 $$T_2 = \displaystyle{1 \over 4C_V} \displaystyle{I_a t \over {\rm \mu}}\comma \; \quad \quad \quad {\rm \rho}_2 = \displaystyle{27 \over 4{\rm \pi}^{1/2}} \displaystyle{{\rm \mu}^{5/2} R_L^2 \over I_a^{3/2} t^{9/2}}.$$
$$T_2 = \displaystyle{1 \over 4C_V} \displaystyle{I_a t \over {\rm \mu}}\comma \; \quad \quad \quad {\rm \rho}_2 = \displaystyle{27 \over 4{\rm \pi}^{1/2}} \displaystyle{{\rm \mu}^{5/2} R_L^2 \over I_a^{3/2} t^{9/2}}.$$Resulting from this we obtain for the ablation pressure
where the ablation pressure for the planar expansion P 0 is given as:
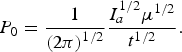 $$P_0 = \displaystyle{1 \over \left(2{\rm \pi} \right)^{1/2}} \displaystyle{I_a^{1/2} {\rm \mu}^{1/2} \over t^{1/2}}.$$
$$P_0 = \displaystyle{1 \over \left(2{\rm \pi} \right)^{1/2}} \displaystyle{I_a^{1/2} {\rm \mu}^{1/2} \over t^{1/2}}.$$For large values of ξ/R L, the solution (29) converts in the self-similar solution for the spherical expansion:
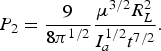 $$P_2 = \displaystyle{9 \over 8{\rm \pi}^{1/2}} \displaystyle{{\rm \mu}^{3/2} R_L^2 \over I_a^{1/2} t^{7/2}}.$$
$$P_2 = \displaystyle{9 \over 8{\rm \pi}^{1/2}} \displaystyle{{\rm \mu}^{3/2} R_L^2 \over I_a^{1/2} t^{7/2}}.$$The ratio ξ/R L (which determines the factor Ψ) for mechanisms of “thermal” ablation due to the electron conductivity and due to fast electrons is described by expressions (22) and (23) (or (24), using the scaling (15) for the fast electron temperature). The expressions for laser-produced plasma parameters at the planar expansion including relations (25)–(31) with reference to (20), (14), (22), and (23), have the following forms with respect to the electron thermal conductivity
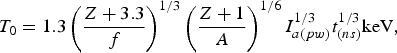 $$T_0 = 1.3\left(\displaystyle{Z + 3.3 \over f} \right)^{1/3} \left(\displaystyle{Z + 1 \over A} \right)^{1/6} I_{a\lpar pw\rpar}^{1/3} t_{\lpar ns\rpar}^{1/3} {\rm keV}\comma \;$$
$$T_0 = 1.3\left(\displaystyle{Z + 3.3 \over f} \right)^{1/3} \left(\displaystyle{Z + 1 \over A} \right)^{1/6} I_{a\lpar pw\rpar}^{1/3} t_{\lpar ns\rpar}^{1/3} {\rm keV}\comma \;$$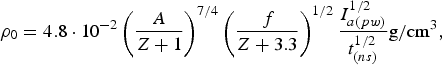 $${\rm \rho} _0 = 4.8 \cdot 10^{ - 2} \left(\displaystyle{A \over Z + 1} \right)^{7/4} \left(\displaystyle{\,f \over Z + 3.3} \right)^{1/2} \displaystyle{I_{a\lpar pw\rpar}^{1/2} \over t_{\lpar ns\rpar}^{1/2}}{\rm g/cm}^3\comma \;$$
$${\rm \rho} _0 = 4.8 \cdot 10^{ - 2} \left(\displaystyle{A \over Z + 1} \right)^{7/4} \left(\displaystyle{\,f \over Z + 3.3} \right)^{1/2} \displaystyle{I_{a\lpar pw\rpar}^{1/2} \over t_{\lpar ns\rpar}^{1/2}}{\rm g/cm}^3\comma \;$$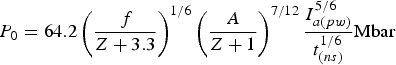 $$P_0 = 64.2\left(\displaystyle{\,f \over Z + 3.3} \right)^{1/6} \left(\displaystyle{A \over Z + 1} \right)^{7/12} \displaystyle{I_{a\lpar pw\rpar}^{5/6} \over t_{\lpar ns\rpar}^{1/6}} \hbox{Mbar}$$
$$P_0 = 64.2\left(\displaystyle{\,f \over Z + 3.3} \right)^{1/6} \left(\displaystyle{A \over Z + 1} \right)^{7/12} \displaystyle{I_{a\lpar pw\rpar}^{5/6} \over t_{\lpar ns\rpar}^{1/6}} \hbox{Mbar}$$and the fast electrons (using scaling (15))
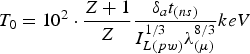 $$T_0 = 10^2 \cdot \displaystyle{Z + 1 \over Z} \displaystyle{{\rm \delta}_a t_{\lpar ns\rpar} \over I_{L\lpar pw\rpar}^{1/3} {\rm \lambda} _{\lpar {\rm \mu} \rpar}^{8/3}} keV$$
$$T_0 = 10^2 \cdot \displaystyle{Z + 1 \over Z} \displaystyle{{\rm \delta}_a t_{\lpar ns\rpar} \over I_{L\lpar pw\rpar}^{1/3} {\rm \lambda} _{\lpar {\rm \mu} \rpar}^{8/3}} keV$$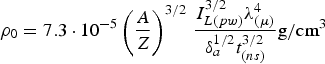 $${\rm \rho} _0 = 7.3 \cdot 10^{ - 5} \left({\displaystyle{A \over Z}} \right)^{3/2}\, \displaystyle{{I_{L\lpar pw\rpar }^{3/2} {\rm \lambda} _{\lpar {\rm \mu} \rpar }^4 } \over {{\rm \delta} _a^{1/2} t_{\lpar ns\rpar }^{3/2} }}{\rm g/cm}^3$$
$${\rm \rho} _0 = 7.3 \cdot 10^{ - 5} \left({\displaystyle{A \over Z}} \right)^{3/2}\, \displaystyle{{I_{L\lpar pw\rpar }^{3/2} {\rm \lambda} _{\lpar {\rm \mu} \rpar }^4 } \over {{\rm \delta} _a^{1/2} t_{\lpar ns\rpar }^{3/2} }}{\rm g/cm}^3$$ $$P_0 = 7.3\left({\displaystyle{A \over Z}} \right)^{1/2}\, \displaystyle{{{\rm \delta} _a^{1/2} I_{L\lpar pw\rpar }^{7/6} {\rm \lambda} _{\lpar {\rm \mu} \rpar }^{4/3} } \over {t_{\lpar ns\rpar }^{1/2} }}{\rm Mbar}$$
$$P_0 = 7.3\left({\displaystyle{A \over Z}} \right)^{1/2}\, \displaystyle{{{\rm \delta} _a^{1/2} I_{L\lpar pw\rpar }^{7/6} {\rm \lambda} _{\lpar {\rm \mu} \rpar }^{4/3} } \over {t_{\lpar ns\rpar }^{1/2} }}{\rm Mbar}$$In Figure 10, the temperature and density on the ablation surface as a function of the focal beam radius for the 3ω (a) and 1ω (b) laser radiation with the energy of 290 J, calculated at the end of laser pulse (t = τL = 0.25 ns) in the case of the real lateral plasma expansion at the Al target and in the case of the planar approximation, are plotted. The dependencies shown in Figure 10a are calculated by means of Eqs. (25)–(31) and (32)–(34) for the ablation induced by the electron conductivity. They demonstrate the influence of the lateral expansion on the plasma state. Obviously, this influence becomes more pronounced for the smaller beam radii. Namely, for R L = 160 µm the values of the density (curve 1) and temperature (curve 3) of the lateral expanding plasma are only slightly smaller than those corresponding to the planar approximation (curves 2 and 4), whereas for R L = 40 µm these values are about 8 and 1.7 times smaller, respectively. In general, the lateral expansion influences strongly on the ablation density. In planar approximation, the decreased beam radius results in the increased density value (in connection with an enhancement of the mass vaporized by the wave of thermal conductivity). In contrast, the effect of lateral expansion leads to a change of the character of the density-on-radius dependence. If the focal spot radius is varied from 160 to 120 µm, the density practically does not change remains close to 0.08 g/cm3, but its reduction to 40 µm results in the density decrease to the value of 0.05 g/cm3, regardless the evaporated mass growth. The temperature grows from the value of 1.4 keV at R L = 160 m to the value of 2.6 keV at R L = 40 m.

Fig. 10. (Color online) Dependencies of the density and temperature of the plasma plume on the ablation surface on the focal spot radius at the laser energy of 290 J for the third (a) and first (b) harmonics. In Figure 10a: curves 1 and 3 — density and temperature for the lateral expanding plasma plume, 2 and 4 — density and temperature for the plane approximation. In Figure 10b: curves 2 and 5 — density and temperature for the lateral expanding plasma plume and energy transport by fast electrons, curves 1 and 6 — density and temperature for the lateral expanding plasma plume and without energy transport by fast electrons, curves 4 and 7 — density and temperature for the plane approximation and energy transport by fast electrons, curves 3 and 8 — density and temperature for the plane approximation without energy transport by fast electrons.
The dependencies shown in Figure 10b are calculated with Eqs. (25)–(31) and (32)–(34) for the radii of 160 and 120 µm that correspond to the thermal conductivity ablation, and with Eqs. (25)–(31) and (38)–(41) for the radii of 80 and 40 µm corresponding to the fast electron ablation. In spite of the lateral expansion effect, these dependencies illustrate a strong influence of the alternate ablation mechanisms on the laser-produced plasma state. A stronger heating of the material by fast electrons (as compared to that due to the thermal conductivity wave) leads to a situation, when the influence of the enhanced mass of the plasma plume exceeds the lateral expansion effect. Consequently, in contrast to results obtained for the 3ω, the weak monotonic decrease of the ablation density with the beam radius dropping from 160 to 80 µm changes to its strong increase up to the value of 0.35 g/cm3 when further reducing the radius to 40 µm. Besides the weak monotonic increase of the temperature with the beam radius decreasing from 160 to 80 µm changes to its decrease down to the value of 0.8 keV for the radius reduced to 40 µm. This explains the results of the spectroscopic measurements and the numerical calculations regarding the temperature drop near the ablation surface for small values of the laser beam radius. In the 1ω case, the decrease of the radius from 160 to 40 µm results in a monotonic increase of the ablation pressure from 28 to 122 Mbar, whereas in the 3ω case it changes weakly being on the level of 50–70 Mbar.
Let us now consider the question of the laser-produced plasma energy transfer to the shock wave, which propagates through the solid part of the target, as well as the question of the crater formation due to the shock wave propagation. The volume of crater created by laser pulse action on light metal surface (in the absence of any substantial energy losses due to thermal radiation) is determined by the relation (Gus'kov et al., Reference Gus'kov and Gus'kov2001):
where σ is the efficiency of absorbed laser energy transfer to the shock wave energy (or when applying the terminology taken from (Gus'kov et al., Reference Gus'kov and Gus'kov2001), the ablation loading efficiency), ɛ is the specific energy required to create a unit mass crater, and the parameter α is a fraction of the thermal energy of the material behind the shock wave front.
The energy transferred into the shock wave per unit time equals to πR 2wP 0 in the case of the planar expansion and πξ2wP 2 in the case of the spherical expansion (where w is the velocity of the material behind the shock wave front). In approximation of the strong shock wave, the ratio of this energy to the energy absorbed in the plasma plume per unit time πR L2I a and the instantaneous values of the ablation loading efficiency for two cases of expansion geometry are given by the formulas
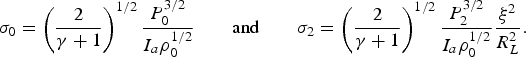 $${{\rm \sigma} _0 = \left({\displaystyle{2 \over {{\rm \gamma} + 1}}} \right)^{1/2} \displaystyle{{P_0^{3/2} } \over {I_a {\rm \rho} _0^{1/2} }} \quad \quad {\rm and} \quad \quad {\rm \sigma} _2 = \left({\displaystyle{2 \over {{\rm \gamma} + 1}}} \right)^{1/2} \displaystyle{{P_2^{3/2} } \over {I_a {\rm \rho} _0^{1/2} }}\displaystyle{{{\rm \xi} ^2 } \over {R_L^2 }}}.$$
$${{\rm \sigma} _0 = \left({\displaystyle{2 \over {{\rm \gamma} + 1}}} \right)^{1/2} \displaystyle{{P_0^{3/2} } \over {I_a {\rm \rho} _0^{1/2} }} \quad \quad {\rm and} \quad \quad {\rm \sigma} _2 = \left({\displaystyle{2 \over {{\rm \gamma} + 1}}} \right)^{1/2} \displaystyle{{P_2^{3/2} } \over {I_a {\rm \rho} _0^{1/2} }}\displaystyle{{{\rm \xi} ^2 } \over {R_L^2 }}}.$$The ablation loading efficiency with taking into account the lateral expansion can be approximated by the formula
where
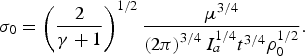 $${\rm \sigma} _0 = \left({\displaystyle{2 \over {{\rm \gamma} + 1}}} \right)^{1/2} \displaystyle{{{\rm \mu} ^{3/4} } \over {\left({2{\rm \pi} } \right)^{3/4} I_a^{1/4} t^{3/4} {\rm \rho} _0^{1/2} }}.$$
$${\rm \sigma} _0 = \left({\displaystyle{2 \over {{\rm \gamma} + 1}}} \right)^{1/2} \displaystyle{{{\rm \mu} ^{3/4} } \over {\left({2{\rm \pi} } \right)^{3/4} I_a^{1/4} t^{3/4} {\rm \rho} _0^{1/2} }}.$$The lateral expansion factor Ř is again determined by Eq. (27) including Eqs. (22)–(24) for the ratio ξ/R L.
In the planar approximation, by using Eqs. (20) and (14) for the ablation loading efficiency in cases of the thermal conductivity ablation and the fast electron ablation we obtain with respect to the scaling (15)
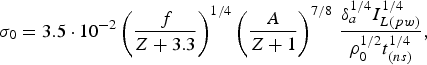 $${\rm \sigma} _0 = 3.5 \cdot 10^{ - 2} \left({\displaystyle{\,f \over {Z + 3.3}}} \right)^{1/4} \left({\displaystyle{A \over {Z + 1}}} \right)^{7/8}\, \displaystyle{{{\rm \delta} _a^{1/4} I_{L\lpar pw\rpar }^{1/4} } \over {{\rm \rho} _0^{1/2} t_{\lpar ns\rpar }^{1/4} }}\comma \;$$
$${\rm \sigma} _0 = 3.5 \cdot 10^{ - 2} \left({\displaystyle{\,f \over {Z + 3.3}}} \right)^{1/4} \left({\displaystyle{A \over {Z + 1}}} \right)^{7/8}\, \displaystyle{{{\rm \delta} _a^{1/4} I_{L\lpar pw\rpar }^{1/4} } \over {{\rm \rho} _0^{1/2} t_{\lpar ns\rpar }^{1/4} }}\comma \;$$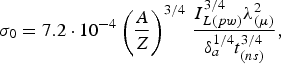 $${\rm \sigma} _0 = 7.2 \cdot 10^{ - 4} \left({\displaystyle{A \over Z}} \right)^{3/4} \,\displaystyle{{I_{L\lpar pw\rpar }^{3/4} {\rm \lambda} _{\lpar {\rm \mu} \rpar }^2 } \over {{\rm \delta} _a^{1/4} t_{\lpar ns\rpar }^{3/4} }}\comma \;$$
$${\rm \sigma} _0 = 7.2 \cdot 10^{ - 4} \left({\displaystyle{A \over Z}} \right)^{3/4} \,\displaystyle{{I_{L\lpar pw\rpar }^{3/4} {\rm \lambda} _{\lpar {\rm \mu} \rpar }^2 } \over {{\rm \delta} _a^{1/4} t_{\lpar ns\rpar }^{3/4} }}\comma \;$$respectively. Figure 11 depicts the ablative loading efficiency and the experimental and theoretical crater volume for the Al target and the laser energy of 290 J as a function of the focal beam radius. These graphs correspond to the 3ω (a) and 1ω (b) laser radiation. The crater volumes were calculated for the thermal conductivity ablation by Eq. (38) with reference to Eq. (42), while for the fast electron ablation Eq. (43) was used. The best agreement between the calculated crater volumes and those obtained experimentally was achieved when inserting the value of αε = 3.7 × 103 J/g in Eq. (38). Bearing in mind the estimation of the unitary thermal energy ε behind the front of the shock wave presented in the previous section, which is on the level of 2.6 × 103 J/g for the Al target, we obtain for the coefficient α the value of 1.5.

Fig. 11. (Color online) Dependencies of the ablative loading efficiency and the crater volume on the focal spot radius at energy of 290 J using the 3ω (a) and 1ω (b) laser radiation. In Figure 11a: curve 1 — ablative loading, curves 2 and 3 (black squares) — theoretical and experimental values of the crater volume. In Figure 11b: curve 1 (black squares) — experimental value of the crater volume, curves 2 and 3 — theoretical values of the crater volume with and without fast electron energy transfer, curves 4 and 5 — the efficiency of the ablative loading with and without the fast electron energy transfer.
In the 3ω case when the ablation occurs due to the thermal conductivity only, the ablation loading efficiency decreases monotonically with the beam radius decrease from the value of 2.1 × 10−2 at R L = 160 µm to the value of 1.1 × 10−2 at R L = 40 µm (Fig. 11a). This results from the effect of lateral expansion. The calculated crater volumes, in analogy to the efficiency of the ablative loading, also monotonically decrease with the decreasing radius. They agree well both qualitatively and quantitatively with the experimental data. Like in the 3ω case, the ablation loading efficiency for the thermal conductivity decreases also for the 1ω due to lateral expansion (Fig. 11b) when the radius is reduced from 160 µm to 80 µm. Since the beam radius reduction from 80 to 40 µm results in the change of the ablation mechanism, the ablation loading efficiency increases and achieves the value of 4.7 × 10−2 at R L = 40 µm which is by a factor of 3 larger than that for the 3ω at the same radius. The calculated dependence of the crater volume on the beam radius Ωcr(R L), which for a given value of the laser energy corresponds to the dependence of the ablation loading efficiency on R L, compares well with the experimentally observed weak changes of the crater volume Ωcr at large radii and its significant increase at small radii. In addition to the general qualitative agreement of theoretical and experimental data, the character of the two quantitative differences of these dependences is even more interesting. Namely, (1) the experimental results demonstrate a much stronger growth of the crater volume (the ablation loading efficiency as well) in the small radii region than that obtained by using the analytical model and (2) this actual growth starts earlier, i.e., already at R L = 120 µm, whereas the theoretical growth starts from the radius of 80 µm only. Both these differences testify that the hydrodynamic mechanism of the crater creation itself is not capable of creating so large craters as those observed experimentally in the case of the 1ω irradiation. This conclusion is in correspondence with the results of numerical simulations described in the previous Section. They showed that in the 1ω case at the beam radius of 40 µm the crater formation, and particularly its peripheral part, is effectuated due to the heating the solid material by fast electrons from a hard part of the energetic spectrum, whose maximal energy reaches a value of 194 keV. The comparative analysis of the experimental and theoretical dependences Ωcr(R L) presented in Figure 11b indicates that the creation of the crater peripheral part due to the heating by fast electrons starts from the radius of 100–110 µm, whereas the ablation mass is still determined by heating the laser-produced plasma via the thermal conductivity wave. It means that such regime of the crater formation becomes efficient when fast electrons from the basic part of the spectrum deposit their energy in the plasma plume, while heating the solid part of the target and the crater is created by fast electrons from the hard tail of the spectrum only.
In the case of the crater formation by the shock wave, the dependence of the crater volume on energetic characteristics of the laser pulse is determined by the absorbed laser energy and the ablative loading efficiency Ωcr∝E aσ, see Eq. (38). Hence in the case of the thermal conductivity ablation and in accordance with Eq. (37), we arrive to Ωcr∝I L5/4. This explains the relatively weak dependence of the experimentally measured crater volume on the intensity (with the exponent of 1.2–1.5 in the exponential approximation) in the 3ω case as well as in the 1ω case for larger radii, i.e., for low intensities (see Section 2.2). For the minimum beam radius of the 1ω radiation, when the crater size is determined by the range of fast electrons from the hard part of the energy spectrum, the dependence of the crater volume on the intensity (I L) turns out to be much stronger than in the case of the hydrodynamic mechanism of the crater formation. Indeed, if the fast electron free path is proportional to the square of the fast electron energy and Ωcr∝E 6, for the scaling E∝I L2/3 applied in this work we obtain Ωcr∝I L4. This dependence is even stronger than that obtained experimentally, where Ωcr∝I L3–3.2. Hence we can conclude that in the experiment the dependence of the fast electron average energy on the intensity corresponds to the scaling E∝I L0.5–0.55. Consequently, the crater measurements provide a possibility to study the spectral composition of fast electrons in the hard part of the spectrum.
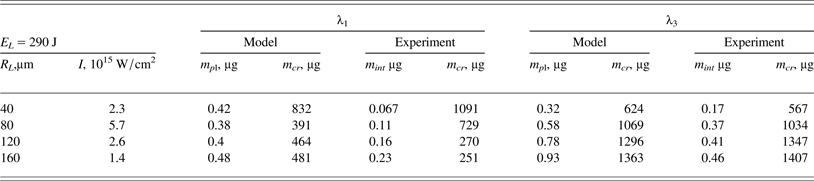
Table 4 presents the comparison of theoretical and experimental results regarding the mass characteristics at all the beam radii used and the energy of 290 J. In the first data set, the values of the total mass of the Al plasma plume m pl = πR L2µ calculated using the theoretical values of the ablation area mass µ (see Table 3) are collected. The second data set presents only the part of the plasma plume mass m int, corresponding to the experimental value of the total electron number N e which was measured in the plasma volume with the density less than critical plasma density (see Table 1 and Figs. 4 and 5). This mass was calculated from the expression m int = N eAm p/Z for the average ion charge Z = +9, which was chosen taking into account the quenching effect. The third data set concerns the theoretical and experimental values of the crater mass m cr = ρ0Ωcr.
Table 4. Comparison of theoretical and experimental results

We note that the mass of the crater material heated to the temperature below 1 eV, is by 2–3 orders of magnitude larger than the mass of the plasma plume with the temperature of a few hundred eV. The theoretical values of the plasma plume mass m pl as well as the experimental values m int decrease with the decreasing laser beam radius for both the harmonics of the laser radiation. Taking into account the decrease of the crater mass with the decreasing beam radius for the 3ω and its increase for the 1ω, one can accept the coincidence of the theoretical predictions with the experimental data related to the ratio N e/Ωcr and, particularly, to the weak change of this ratio for the 3ω and its strong rise with decreasing beam radius in the 1ω case. The physical reason for this consists in the influence of the fast electrons on the crater formation, which leads to the increase of its volume with the decreasing beam radius, regardless the influence of lateral expansion of the laser-produced plasma.
The developed model provides a possibility to describe in a simple analytical form the state of plasma plume and the shock wave generation in the solid target under the conditions used in the experiment. Let us discuss the experimental results obtained on Al targets at energies of 120 and 580 J as well as those obtained for Cu targets from the point of view of the analytical model. In the beginning, let us consider the influence of the variable laser energy on results of experiments with Al targets. In the 3ω case, the effect of the fast electron energy transfer does not play any role, neither in the process of the plasma plume formation nor in the shock wave generation and the crater formation processes. The dependence of the crater volume decrease with the decreasing beam radius at the energy of 120 J practically repeats the dependence found for the energy of 290 J with almost identical ratios of the crater volumes (approximately equal to 0.35). According to Eq. (22), for the thermal conductivity ablation, the ratio of the plasma plume dimension to the beam radius depends weakly on the laser energy (as E L1/6), therefore the effect of lateral expansion for the same beam radius plays almost identical role in both the cases. Thus, according to Eq. (42), the ratio of craters volumes is determined by the ratio of energies as well as by the ratio of ablation loading efficiencies σ1D calculated using the planar approximation. For the thermal conductivity ablation, according to Eq. (42) σ0∝I 1/4. This is why for two experiments using the 3ω laser radiation with energies of E L1 and E L2 at the same values of the beam radius and the pulse duration, the ratio of crater volumes can roughly be expressed by the relation (E L1/E L2)5/4, which for the considered example corresponds to a value of 0.33.
In the 1ω case, the experimental results were obtained for energies of 120, 290 and 580 J. Due to the fast electron energy transport at radii smaller than 100–120 µm, the crater volume increases with the decreasing beam radius. For different energies, it is interesting to compare the ratio of the crater volume Ωmax obtained using the radius of 40 µm, i.e., at the maximal laser intensity corresponding to the maximum effect of fast electrons, to the crater volume Ωmin obtained at the radius of 160 µm, i.e., at the minimal intensity when the fast electron influence is practically negligible. The ratio Ωmax/Ωmin increases with the increasing energy, thus confirming the increasing importance of the fast electrons role. Its values amount to 2.9, 3.4, and 17.4 for the energies of 120 J, 290 J, and 580 J, respectively. At approximately the same rise in the energy by the transition from 120 to 290 J (2.4-fold increase) and from 290 to 580 J (two-fold increase), the ratio Ωmax/Ωmin increases much larger for the latter transition — about 5.1 times, than the former one — only 1.5 times. Obviously, the relatively small increase of the ratio Ωmax/Ωmin at the energy transition from 120 to 290 J corresponds to the increase of the ablation loading efficiency followed by the growth of the fast electron average energy at small beam radii. Meanwhile, much larger increase of the ratio Ωmax/Ωmin at the energy transition from 290 J to 580 J, which considerably exceeds the increase of the ablation loading efficiency with the increasing average energy of fast electrons, means that at 580 J of the laser energy a larger part of the crater is formed via direct heating the solid target by fast electrons from the hard part of the spectrum. The volume of the peripheral part of the crater created by the direct fast electron heating considerably exceeds (2–3 times) the volume of the crater part formed due to the shock wave driven by the electrons with the average energy.
In the experiments with Cu targets, the dependencies of the crater volume on the beam radius obtained for all values of the laser energy and the same frequency correspond qualitatively to those observed on Al targets. Analogously, they demonstrate a large influence of the fast electron energy transport on both the state of the plasma plume and the crater formation. Simultaneously, at irradiation conditions under which the role of fast electron ablation is small (in the 3ω case in the whole range of radii and energies used, whereas in the 1ω case at larger beam radii and energies of 120 and 290 J only), the crater volumes produced in Cu and Al targets are in the same relation to the ratios of both the density and critical temperature of target materials, as well as to the ratios of coefficients of the laser radiation absorption and the ablation loading efficiencies. Indeed, according to (34), the ratio of crater volumes at the same energy can be expressed as
Next, using Eq. (37) for the ablation loading efficiency in the material heated by the thermal conductivity wave and taking into account the fact that εAl/εCu ≈ 1.6, we obtain
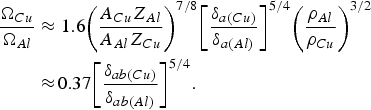 $$\eqalign{\displaystyle{{{\Omega _{Cu}}} \over {{\Omega _{Al}}}} & \approx 1.6{\left({\displaystyle{{{A_{Cu}}{Z_{Al}}} \over {{A_{Al}}{Z_{Cu}}}}} \right)^{7/8}}{\left[{\displaystyle{{{{\rm \delta} _{a\lpar Cu\rpar }}} \over {{{\rm \delta} _{a\lpar Al\rpar }}}}} \right]^{5/4}}{\left({\displaystyle{{{{\rm \rho} _{Al}}} \over {{{\rm \rho} _{Cu}}}}} \right)^{3/2}} \cr & \approx \!0.37{\left[{\displaystyle{{{{\rm \delta} _{a\lpar Cu\rpar }}} \over {{{\rm \delta} _{a\lpar Al\rpar }}}}} \right]^{5/4}}.}$$
$$\eqalign{\displaystyle{{{\Omega _{Cu}}} \over {{\Omega _{Al}}}} & \approx 1.6{\left({\displaystyle{{{A_{Cu}}{Z_{Al}}} \over {{A_{Al}}{Z_{Cu}}}}} \right)^{7/8}}{\left[{\displaystyle{{{{\rm \delta} _{a\lpar Cu\rpar }}} \over {{{\rm \delta} _{a\lpar Al\rpar }}}}} \right]^{5/4}}{\left({\displaystyle{{{{\rm \rho} _{Al}}} \over {{{\rm \rho} _{Cu}}}}} \right)^{3/2}} \cr & \approx \!0.37{\left[{\displaystyle{{{{\rm \delta} _{a\lpar Cu\rpar }}} \over {{{\rm \delta} _{a\lpar Al\rpar }}}}} \right]^{5/4}}.}$$The coefficient of the laser energy transformation into the plasma internal energy for copper is smaller than that for aluminum due to larger energy losses by the plasma radiation. According to (Gus'kov et al., Reference Gus'kov, Kasperczuk and Pisarczyk2007), for the target irradiation conditions used at the PALS laser, the ratio δa(Cu)/δa(Al) is in the range of 0.6–0.7, whereas the ratio of craters volumes ΩCu/ΩAl lays within the range of 0.2–0.25.
5. CONCLUSIONS
Based on the results presented in this work, the following conclusions referring to the efficiency of the energy transfer from the plasma plume to the shock wave and to the role of fast electrons in this process could be made. At the laser intensity of 1–20 PW/cm2 and the coupling parameter of 2 × 1014−4 × 1015 Wµm2/cm2 that corresponds to the fast electron energy of 20 keV (generated in experiments using the laser pulse energy of 120–290 J for the 3ω radiation of the PALS iodine laser), the dominant mechanism of the target material ablation during the period of 250 ps is the heating by the thermal conductivity wave. In addition, under conditions of the lateral expansion the ablation pressure increases from 50 Mbar for the intensity of 1 PW/cm2 to 70 Mbar for the intensity of 20 PW/cm2, whereas the efficiency of the laser energy transformation into the shock wave energy is on the level of 1–2.5%.
At the laser intensity of 10–50 PW/cm2 (at the coupling parameter of 1016−5 × 1016 Wm2/cm2) relevant to the laser spike intensity in the impact ignition approach, the average fast electron energy is larger than 50 keV (the experiments with the laser pulse energy of 290–580 J for the first harmonic of the PALS iodine laser radiation) and the dominant mechanism of the target material ablation during the period of 250 ps is the heating by fast electrons. Besides, at conditions of the lateral expansion, the ablative pressure increases from 100 Mbar for the intensity of 10 PW/cm2 to 300 Mbar for the intensity of 50 PW/cm2, whereas the efficiency of the laser energy transformation into the shock wave energy is on the level of 2–7%.
ACKNOWLEDGMENTS
The participation of S. Yu. Gus'kov and N.N. Demchenko in this work was supported by RFBR projects No 12-02-92101-JF, No 14-02-00010, and No 13-02-00295. The activities of O. Renner and M. Smid were supported by Academy of Sciences of the Czech Republic project M100101208 and by the Czech Science Foundation under the project CZ.1.07/2.3.00/20.0279. This research was also supported in part by by LASERLAB--EUROPE (EU Contract No. 284464), by the National Center of Science (NCN), Poland under Grant No 2012/04/M/ST2/00452, and by the Czech Republic's Ministry of Education, Youth and Sports under PALS RI project (LM2010014).