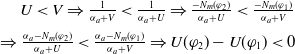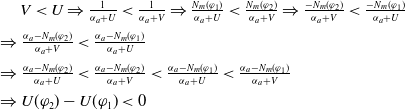1. Introduction
We can assume that during the process of communication or dialog between two people, at least at some point, one has an idea of the beliefs and goals of the other. Of course, these ideas may not correspond to the perfect reality, but this does not prevent them from having a conversation or a debate and thus deciding what to say or not to say. The same assumption can be made about the interaction between a user and a machine (Hollnagel & Woods, Reference Hollnagel and Woods1983) or even between a user and an information retrieval (IR) system during an interactive IR process (Belkin, Reference Belkin1992). This is the main motivation of our proposal. Indeed, we propose three measures of information usefulness that consider the IR system as a cognitive agent (Rao & Georgeff, Reference Rao and Georgeff1991). This agent has beliefs about the information that the user—who is also considered as a cognitive agent—needs to achieve his/her goals. Our final aim is to help provide the users with documents that help them achieve an informative goal or accomplish a task.
As pointed out by Xu and Yin (Reference Xu and Yin2008), ‘The information science research community is characterized by a paradigm split, with a system-centered cluster working on IR algorithms and a user-centered cluster working on user behavior. The two clusters rarely leverage each other’s insight and strength’. Most of the existing works dealing with the ‘system’s view about the user needs’ are essentially based on the user profile (or on the past behavior of other users), whose contents are the user’s interests, preferences, etc., acquired from the user’s past interactions with the system (Stewart & Davies, Reference Stewart and Davies1997; Schiaffino & Amandi, Reference Schiaffino and Amandi2009). Overall, as it has been recently pointed out by Vakkari et al. (Reference Vakkari, Völske, Potthast, Hagen and Stein2019), the existing studies typically focused on perceived usefulness rather than on actual use of the piece of information by the user. While this is adapted to represent the user’s interests in general, it may not be adapted to represent the user’s current needs especially if the user is looking for novelty in information to be used to achieve a given goal—I was interested in a washing machine until the last week when I bought one; now, while it is part of my past interests, I am not interested in it anymore because I already achieved my goal. The user profile represents, for sure, the user past interests, and in the cases in which the research for information is not related to a particular goal, it can be that the user is still looking for the same or similar piece of information. In this paper, we are interested in modeling the usefulness of information for information retrieval goal-driven users. Therefore, a piece of information is considered useful by the user if and only if it is new with respect to what the user already knows, and it helps the user to achieve his/her current goals.
We have recently proposed in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019) a general logic-based framework in which there are two cognitive agents: one is the user who has some beliefs and some goals modeled as propositional formulas; the second is the system, which has some beliefs about the user’s beliefs and goals. This framework aims at providing the user with information which is the most useful for him/her to achieve his/her own goals. The proposed framework is general enough to model the paradigm of cooperative exchanges with a system (a speaker, a database, the search engine) that answers the query expressed by the user (the listener, the database user, the web user…) and has to provide the most useful information to the user. The definition of the concept of information usefulness in such a context takes the system point of view and tries to characterize how useful a piece of information can be for the user.
However, in such a framework there are some limitations which could prevent its use in many real-world situations. For example, it is assumed that there is only one way to achieve a goal, that is, each goal has exactly one conjunction of literals allowing its achievement. Here, we propose a solution to relax this hypothesis by assuming that a goal can be achieved in different ways. We extend the three definitions of usefulness, that is the binary approach, the ordinal approach and the numerical approach, proposed in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019), and prove that the new proposed definitions are indeed a generalization of the definitions proposed therein.
The article is organized as follows. In Section 2, we present some related work by underlining the differences with what we are proposing here. In Section 3, we give some preliminaries and state some basic definitions. In Sections 4, 5, and 6, we propose three different definitions of information usefulness and their extensions, respectively, called binary, ordinal, and numerical. In Section 7, we consider the particular case of IR and compare some measures defined there with ours. Some concluding remarks are given in Section 8.
2. Related work
In IR, the aim is to take into account a query expressed by a user and provide documents which best suit the user request. In system-centered IR paradigms, the topical-relevance-based approach is considered. In this case, the relevant documents are those whose topics best match the topics of the user query (Huang & Soergel, Reference Huang and Soergel2013)—this led to the aboutness or topicality measure.
User-centered systems have also been proposed. Those systems consider (also) other dimensions to assess the usefulness of a document for the user, for example: coverage, which measures how strongly the user interests are included in a document (Pasi et al., Reference Pasi, Bordogna and Villa2007); appropriateness, which measures how suitable a document is with respect to the user interests (da Costa Pereira et al., Reference da Costa Pereira, Dragoni and Pasi2012); and novelty, which measures how novel the document is with respect to what the system has already proposed to the user (Clarke et al., Reference Clarke, Kolla, Cormack, Vechtomova, Ashkan, Büttcher and MacKinnon2008). However, works considering explicitly the fact that the users behave as cognitive agents are still rare. A good start in this direction has been proposed by Belhassen et al. (Reference Belhassen, Abdallah and Ben Ghezala2000), but, unfortunately, the authors did not follow up on their work. It is indeed believed that users behave as cognitive agents (Mizzaro, Reference Mizzaro1996; Sutcliffe & Ennis, Reference Sutcliffe and Ennis1998; Culpepper et al., Reference Culpepper, Diaz and Smucker2018) having their own beliefs and knowledge about the world. They try to fill their information gaps (missing or uncertain information) by conducting information search activities. Users interact with search systems by submitting queries expecting to receive new or ‘relevant’ information that will help them reach their search goal and thus reduce their information gaps.
In Social Science, studying how people achieve effective conversational communication in common social situations is needed. In this area, Grice (Reference Grice, Cole and Morgan1975), introduced the maxim of quantity which emphasizes the fact that a speaker contribution must be as informative as required for the current purposes of the exchange, but not more informative. Xu and Chen (Reference Xu and Chen2006) considered IR as an indirect form of human comunication and chose Grice’s maxims on human communication as the theoretical foundation to identify the relevance criterion. Their study was based on a cognitive approach and focused on the criteria users employ to estimate the document’s relevance judgment beyond aboutness. Five criteria, in line with Grice’s maxims, have been considered in Xu and Chen (Reference Xu and Chen2006): scope, novelty, topicality, reliability, and understandability. Scope has been defined as the ‘extent to which the topic or content covered in a retrieved document is appropriate to the user’s need’. Novelty, instead, has been defined as the ‘extent to which the content of a retrieved document is new to the user or different from what the user has known before’. This implicitly assumes that the user’s previous knowledge can somehow be represented. Topicality has been defined as the ‘extent to which a retrieved document is perceived by the user to be related to her current topic of interest’; Reliability has been defined as the ‘degree to which the content of a retrieved document is perceived to be true, accurate, or believable’ while understandability has been defined as the ‘extent to which the content of a retrieved document is perceived by the user as easy to read and understand’. The results obtained show that, among the five proposed criteria, only the scope criterion is not supported by the data. Besides, the results suggested that topicality and novelty criteria are the two factors that are most significant to judge if a document is relevant to the user. Some limitations of the study have been pointed out by the authors. Indeed, they assumed an additive model to compute the overall relevance based on the five considered criteria. They left out of their studies non-topical relevant documents. However, in other contexts where non-topical documents are also considered, non-additive models, such as a multiplicative model, might be considered. Another problem raised by this choice of an additive model is that when the cognitive aspects are considered, a relevant document is not one that is just on topic.
The change it introduces to the current cognitive state is also indispensable. Such cognitive change is the heart of relevance as a potentially dynamic subjective notion. Because cognitive change hinges on novelty, relevance would be a static concept without novelty.
In this paper, we take this fact into account by considering an achievement goal as representing what the user needs in terms of information to achieve a given task. We represent it as a rule with a list of pieces of information needed in its left-hand side and the goal in its right-hand side. Because we do not consider the ‘forgetting’ possibility, if the user becomes aware of a piece of information they will not forget it. This means that if the user obtains the same information again, it will not contribute to help achieving any goal—not useful anymore. On the contrary, an acquired piece of information which is in the left-hand side of a rule but novel, that is, not yet ‘known’ by the user, is considered useful. To summarize, when the retrieved piece of information is to be used to help accomplishing a task related to an informative goal, the novelty of the piece of information is an important factor to decide about its utility or usefulness. The representation of the rules we have used to represent informative goals is inspired by the Jason’s planning rules (Bordini et al., Reference Bordini, Hübner and Wooldridge2007). More precisely, we have used the extension of Jason rules we have recently proposed in Zein and da Costa Pereira (Reference Zein and da Costa Pereira2022). The difference between the original Jason’s rules and our rules is essentially due to the fact that the plan execution in Jason is reliant on the occurrence of the triggering event. While it is adapted for action plans is it not adapted for representing updating beliefs.
Belkin et al. (Reference Belkin, Oddy and Brooks1982) defined the concept of ‘Anomalous State of Knowledge (ASK)’ as the state representing what is wrong in the user’s knowledge, that is, what is missing in the user’s knowledge base that prevents him/her to achieve his/her goals or tasks—this is at the basis of the information need. Belkin stressed also the fact that in general, the user is not in a position to specify precisely what he or she needs to resolve the anomaly, hence it is more suitable to describe the anomaly rather than asking the user to specify his/her need as a request to the system. Hollnagel (Reference Hollnagel1980), argued that the use of the word ‘Anomalous’ was misleading. According to the author ‘there really is nothing anomalous about not knowing something’. He suggested to rename the paradigm as the Incomplete state of knowledge while Reid (Reference Reid2000) suggested to name it as a knowledge gap. More recently, Belkin recognized that the research in IR should address more directly the user, as a central actor in the IR system. He has very well pointed out in Belkin (Reference Belkin2015) that:
For many years, the field of IR has accepted something like ‘the provision of relevant documents’ as the goal of its systems. This goal has served us quite well, for quite some time, but it is quite different from the goal of ‘the support of people in achievement of the goal or task which led them to engage in information seeking’.
In the multi-agent systems domain, the problem of pursuing an agent’s goals in the absence of certain beliefs needed to achieve them has recently been addressed by Chhogyal et al. (Reference Chhogyal, Consoli, Ghose and Dam2020). They introduced the notion of information-seeking actions in the BDI (Belief-Desire-Intentions) framework to help address these information needs and show how they can be exploited by the agent to increase the expected utility of its goals. While this work can be considered relevant to our work, the main aim is not the same. They use informative actions to fulfill the requirements for achieving the user’s goals while we are also interested in which requirements help the most the user to achieve a given goal and propose the documents helping closing the user’s knowledge gap. Our idea of measuring the usefulness of information can then be seen as a measure of the progress or advancement of the agent’s knowledge toward satisfying the informative goal. A similar idea has been recently treated in a different context by Harland et al. (Reference Harland, Thangarajah and Yorke-Smith2022) to quantify the progress of goals in intelligent agents.
Search-as-Learning (SAL) (Collins-Thompson et al., Reference Collins-Thompson, Hansen and Hauff2017) is a new field that examines user search sessions with learning intent. Among the current challenges for studying SAL identified by Hoppe et al. (Reference Hoppe, Holtz, Kammerer, Yu, Dietze and Ewerth2018), we have the recommendation that the process of ranking the results to be proposed to the user ‘should consider the actual knowledge state of a user and his/her learning intent’. This implies the need of an explicit representation of both the user knowledge as well as the user informative goal.
To the best of our knowledge, apart from the work we are extending here (Cholvy & da Costa Pereira, Reference Cholvy and da Costa Pereira2019), there is no approach in any of the above-mentioned fields that proposes a framework that represents an IR system as a cognitive agent endowed with an explicit representation of the user as an information-seeking cognitive agent looking for information to fill a gap in its knowledge. for explicitly representing an information-seeking user as a cognitive agent seeking information to fill a gap in its knowledge. We propose an improved representation of the IR system as a cognitive agent, with the ability to measure the usefulness of a piece of information to help another cognitive agent, representing the user, bridge the knowledge gap between its current and desired state of knowledge. We propose indeed an improvement of the representation of the user as a cognitive agent endowed with the capacity of measuring the usefulness of a piece of information to help it fill the knowledge gap between its current knowledge state and the desired knowledge state. We extend the three definitions of information usefulness we proposed in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019). A particular added value of our proposal is that the numerical based measure presented in Section 6 allows to capture in a single value different dimensions which have an impact in the relevance measure of a document, without the need for eliciting an explicit priority order on those dimensions, unlike in da Costa Pereira et al. (Reference da Costa Pereira, Dragoni and Pasi2012). In that work, a model based on the aggregation of the satisfaction degrees of the different dimensions has been considered. In addition, a priority was associated to the different dimensions which requires explicit weights for each criterion by the user. Here, given a piece of information, we account, in one single measure, for what is needed and provided by a piece of information, what is not useful and what is still missing to achieve a goal. We do not need priorities.
3. Extending previous definitions: a preliminary step
In this section, we present the extensions we made to the definitions proposed in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019). To understand these extensions, we need to go back and present some of the original definitions.
3.1. Languages
In this section we present the languages we used throughout the paper.
Definition 1 Let A be a set of atomic propositions and let L be the propositional language such that
![]() $A \cup \{\top, \bot\} \subseteq L$
, and,
$A \cup \{\top, \bot\} \subseteq L$
, and,
![]() $\forall \phi, \psi \in L$
,
$\forall \phi, \psi \in L$
,
![]() $\neg \phi \in L$
,
$\neg \phi \in L$
,
![]() $\phi \wedge \psi \in L$
,
$\phi \wedge \psi \in L$
,
![]() $\phi \vee \psi \in L$
.
$\phi \vee \psi \in L$
.
The agent’s beliefs and goals can be represented as formulas in L. However, it can be the case that two different atoms, one representing a belief and the other a goal, have the same English translation. For example, the atom for ‘know modal logic’ as a goal should be different from the atom for ‘know modal logic’ as a belief, although their English translations are the same. We made the choice of using two separate languages to avoid to use modal logic and then have an unnecessarily complicated formalism.
We consider
![]() $L_G$
a subset of language L used to represent the goals. Let a be an agent. We assume the following:
$L_G$
a subset of language L used to represent the goals. Let a be an agent. We assume the following:
-
Agent a has a goal set
 $G_a = \{g_1,..,g_n\}$
, each
$G_a = \{g_1,..,g_n\}$
, each
 $g_i$
being a positive literal of language
$g_i$
being a positive literal of language
 $L_G$
. For instance finish my paper, prepare Monday’s class.
$L_G$
. For instance finish my paper, prepare Monday’s class. -
Agent a has a belief base
 $B_a$
composed of two subsets
$B_a$
composed of two subsets
 $B_a^W$
and
$B_a^W$
and
 $B_a^G$
.
$B_a^G$
.-
–
 $B_a^W$
is the set of formulas from
$B_a^W$
is the set of formulas from
 $L \setminus L_G$
which represent a
′s beliefs about the state of the world, such as for example, I know modal logic, I don’t know the Python language, if I read such book I will know BDI.
$L \setminus L_G$
which represent a
′s beliefs about the state of the world, such as for example, I know modal logic, I don’t know the Python language, if I read such book I will know BDI. -
–
 $B_a^G$
is a set of formulas of L which represent the beliefs of agent a about the different ways to achieve its goals. It is defined as follows: For each
$B_a^G$
is a set of formulas of L which represent the beliefs of agent a about the different ways to achieve its goals. It is defined as follows: For each
 $g \in G_a$
there are
$g \in G_a$
there are
 $n_{g}$
(
$n_{g}$
(
 $n_{g} \geq 1$
) formulas in
$n_{g} \geq 1$
) formulas in
 $B_a^G$
of the form:
$B_a^G$
of the form:
 $premise^1(g) \rightarrow g$
, …,
$premise^1(g) \rightarrow g$
, …,
 $premise^{n_{g}}(g) \rightarrow g$
, where each
$premise^{n_{g}}(g) \rightarrow g$
, where each
 $premise^k(g)$
is a conjunction of positive literals of
$premise^k(g)$
is a conjunction of positive literals of
 $L \setminus L_G$
and called the
$L \setminus L_G$
and called the
 $k^{th}$
premise of g. For example, to finish my state of the art (g), I need knowledge about modal logic (p) or BDI agents (q) (i.e.,
$k^{th}$
premise of g. For example, to finish my state of the art (g), I need knowledge about modal logic (p) or BDI agents (q) (i.e.,
 $p \rightarrow g$
,
$p \rightarrow g$
,
 $q \rightarrow g$
).
$q \rightarrow g$
).
-
3.2. Basic notions
We will define the concept of missing information which is a formula containing the pieces of information the agent needs in order to be able to achieve a goal. The main idea is that with the arrival of new (maybe relevant) information, the amount of missing information should reduce and never increase. Therefore, the more a piece of information allows to reduce the missing information the more useful it is for the user. We will then be led to compare formulas before and after receiving some information in order to measure the usefulness of the new piece of information.
The extension we are proposing here will consider different ways to achieve a goal. We represent those different ways as a disjunction of conjunctions, one conjunction corresponding to one way to achieve a goal. We need then to define a notion of inclusion for disjunctions of conjunctions. Two different types of inclusion will be considered. The first is related to the literals contained in the formulas and the second to the number of literals contained in a formula.
We would like to stress that our formalism is not supposed to consider what happens after the goal has been achieved. We made the hypothesis that as soon as the agent has the necessary information to reach its goal it will not look for that information anymore—we do not consider the forgetting aspect.
In the following definitions, the term ‘literal’ means ‘literal of a propositional language’ (Buss, Reference Buss1998).
Definition 2
-
Let us consider two conjunctions of literals C and C′. We define C as being included in C′, noted
 $C \subseteq C'$
, if and only if all the literals in C are also in C′.
$C \subseteq C'$
, if and only if all the literals in C are also in C′.
 $C \subset C'$
if and only if
$C \subset C'$
if and only if
 $C \subseteq C'$
but
$C \subseteq C'$
but
 $C \not= C'$
. C is equal to C′, noted
$C \not= C'$
. C is equal to C′, noted
 $C = C'$
, if and only if the literals of C are exactly the same as the literals of C′. The result of the intersection between C and C′, noted
$C = C'$
, if and only if the literals of C are exactly the same as the literals of C′. The result of the intersection between C and C′, noted
 $C \cap C'$
, contains literals which are both in C and in C′. The result of the difference between C and C′, noted
$C \cap C'$
, contains literals which are both in C and in C′. The result of the difference between C and C′, noted
 $C \setminus C'$
, contains literals which are in C but not in C′. The cardinality of a conjunction of literals C, noted
$C \setminus C'$
, contains literals which are in C but not in C′. The cardinality of a conjunction of literals C, noted
 $|C|$
, corresponds to the number of literals in C.
$|C|$
, corresponds to the number of literals in C. -
Let D be a disjunction of conjunctions of literals.
 $C \in D$
means that C is one of the conjunctions of D.
$C \in D$
means that C is one of the conjunctions of D. -
Let D and D′ be two disjunctions of conjunctions of literals.
 $D \subseteq D'$
if and only if
$D \subseteq D'$
if and only if
 $\ \forall C \in D$
$\ \forall C \in D$
 $\exists C' \in D'$
st
$\exists C' \in D'$
st
 $C \subseteq C'$
.
$C \subseteq C'$
.
 $D \subset D'$
if and only if
$D \subset D'$
if and only if
 $D \subseteq D'$
but
$D \subseteq D'$
but
 $D' \not\subseteq D$
that is,
$D' \not\subseteq D$
that is,
 $\forall C \in D$
$\forall C \in D$
 $\exists C' \in D'$
st
$\exists C' \in D'$
st
 $C \subseteq C'$
and
$C \subseteq C'$
and
 $\exists C'_{\!\!0} \in D'$
st
$\exists C'_{\!\!0} \in D'$
st
 $\forall C \in D\; C'_{\!\!0} \not\subseteq C$
.
$\forall C \in D\; C'_{\!\!0} \not\subseteq C$
.
Equipped with this notion of formula inclusion, we can now define a preference relation over disjunctions of conjunctions based on it.
Definition 3 Let S and S′ be two sets of disjunctions of conjunctions of positive literals.
![]() $S \preceq^1 S'$
if and only if (i)
$S \preceq^1 S'$
if and only if (i)
![]() $ |S|\leq|S'|$
and (ii) if
$ |S|\leq|S'|$
and (ii) if
![]() $|S|=|S'|$
then there is a bijection
$|S|=|S'|$
then there is a bijection
![]() $f\;:\; S \rightarrow S'$
such that:
$f\;:\; S \rightarrow S'$
such that:
![]() $\forall D \in S\;D \subseteq f(D)$
.
$\forall D \in S\;D \subseteq f(D)$
.
![]() $S \prec^1 S'$
if and only if
$S \prec^1 S'$
if and only if
![]() $S \preceq^1 S'$
and
$S \preceq^1 S'$
and
![]() $S' \not\preceq^1 S$
.
$S' \not\preceq^1 S$
.
In some settings, the above preference relation might be too strong. For this reason, we now define a weaker notion of formula inclusion, which only cares about the number of literals they contain, and which will be used to define a weaker preference relation.
Definition 4 Let D and D′ be two disjunctions of conjunctions of literals. We write
![]() $D \sqsubseteq D'$
if and only if
$D \sqsubseteq D'$
if and only if
![]() $\forall C \in D$
$\forall C \in D$
![]() $\exists C' \in D'$
such that
$\exists C' \in D'$
such that
![]() $\mid C \mid \leq \mid C'\mid $
.
$\mid C \mid \leq \mid C'\mid $
.
![]() $D \sqsubset D'$
if and only if
$D \sqsubset D'$
if and only if
![]() $D \sqsubseteq D'$
but
$D \sqsubseteq D'$
but
![]() $D' \not\sqsubseteq D$
that is,
$D' \not\sqsubseteq D$
that is,
![]() $\forall C \in D$
$\forall C \in D$
![]() $\exists C' \in D'$
st
$\exists C' \in D'$
st
![]() $\mid C \mid \leq \mid C'\mid $
and
$\mid C \mid \leq \mid C'\mid $
and
![]() $\exists C'_{\!\!0} \in D'$
st
$\exists C'_{\!\!0} \in D'$
st
![]() $\forall C \in D\; \mid C'_{\!\!0}\mid \gt \mid C \mid$
.
$\forall C \in D\; \mid C'_{\!\!0}\mid \gt \mid C \mid$
.
Obviously,
![]() $D \subseteq D'$
implies
$D \subseteq D'$
implies
![]() $D \sqsubseteq D'$
. But the contrary is not true. Indeed,
$D \sqsubseteq D'$
. But the contrary is not true. Indeed,
![]() $p \vee q \sqsubseteq (r \wedge s)$
but
$p \vee q \sqsubseteq (r \wedge s)$
but
![]() $p \vee q \not\subseteq (r \wedge s)$
. Moreover,
$p \vee q \not\subseteq (r \wedge s)$
. Moreover,
![]() $D \subset D'$
implies
$D \subset D'$
implies
![]() $D \sqsubset D'$
but the contrary is not true. Indeed, we have
$D \sqsubset D'$
but the contrary is not true. Indeed, we have
![]() $p \vee q \sqsubset (r \wedge s)$
but
$p \vee q \sqsubset (r \wedge s)$
but
![]() $p \vee q \not\subset (r \wedge s)$
.
$p \vee q \not\subset (r \wedge s)$
.
We are now ready to define a weaker preference relation, based on
![]() $\sqsubseteq$
, which we will name
$\sqsubseteq$
, which we will name
![]() $\preceq^2$
.
$\preceq^2$
.
Definition 5 Let S and S′ be two sets of disjunctions of conjunctions of positive literals.
![]() $S \preceq^2 S'$
if and only if (i)
$S \preceq^2 S'$
if and only if (i)
![]() $|S| \leq |S'|$
and (ii) if
$|S| \leq |S'|$
and (ii) if
![]() $|S| = |S'|$
then there is a bijection
$|S| = |S'|$
then there is a bijection
![]() $f\;:\; S \rightarrow S'$
such that:
$f\;:\; S \rightarrow S'$
such that:
![]() $\forall D \in S\; D \sqsubseteq f(D)$
.
$\forall D \in S\; D \sqsubseteq f(D)$
.
![]() $S \prec^2 S'$
if and only if
$S \prec^2 S'$
if and only if
![]() $S \preceq^2 S'$
and
$S \preceq^2 S'$
and
![]() $S' \not\preceq^2 S$
.
$S' \not\preceq^2 S$
.
Thus,
![]() $S \preceq^1 S'$
(resp.,
$S \preceq^1 S'$
(resp.,
![]() $S \preceq^2 S'$
) if and only if S does not have more elements than S
′; if S and S
′ have the same number of elements, then the disjunctions in S are included in the disjunctions of S
′ (resp., are less complex than those of S
′).
$S \preceq^2 S'$
) if and only if S does not have more elements than S
′; if S and S
′ have the same number of elements, then the disjunctions in S are included in the disjunctions of S
′ (resp., are less complex than those of S
′).
Let us notice that:
-
 $\preceq^1$
is a preorder but not total. Some sets of disjunctions of conjunctions are incomparable, such as
$\preceq^1$
is a preorder but not total. Some sets of disjunctions of conjunctions are incomparable, such as
 $\{p, q \wedge r\} \not\preceq^1 \{r, s\}$
and
$\{p, q \wedge r\} \not\preceq^1 \{r, s\}$
and
 $\{r, s\} \not\preceq^1 \{p, q \wedge r\}$
.
$\{r, s\} \not\preceq^1 \{p, q \wedge r\}$
. -
 $\preceq^2$
is a preorder but not total. For instance,
$\preceq^2$
is a preorder but not total. For instance,
 $\{p \vee (q \wedge r), q \wedge r\} \not\preceq^2$
$\{p \vee (q \wedge r), q \wedge r\} \not\preceq^2$
 $\{p \vee q, q \vee (r \wedge s)\}$
and
$\{p \vee q, q \vee (r \wedge s)\}$
and
 $ \{p \vee q, q \vee (r \wedge s)\} \not\preceq^2 \{p \vee (q \wedge r), q \wedge r\}$
.
$ \{p \vee q, q \vee (r \wedge s)\} \not\preceq^2 \{p \vee (q \wedge r), q \wedge r\}$
. -
 $S \preceq^1 S'$
implies
$S \preceq^1 S'$
implies
 $S \preceq^2 S'$
but the contrary is not true in general.
$S \preceq^2 S'$
but the contrary is not true in general. -
 $S \prec^1 S'$
if and only if (i)
$S \prec^1 S'$
if and only if (i)
 $ |S| \lt |S'|$
or (ii)
$ |S| \lt |S'|$
or (ii)
 $|S|=|S'|$
and there is a bijection
$|S|=|S'|$
and there is a bijection
 $f\;:\; S \rightarrow S'$
such that:
$f\;:\; S \rightarrow S'$
such that:
 $\forall D \in S\;D \subseteq f(D)$
and
$\forall D \in S\;D \subseteq f(D)$
and
 $\exists D_0 \in S$
such that
$\exists D_0 \in S$
such that
 $D_0 \subset f(D_0)$
.
$D_0 \subset f(D_0)$
. -
 $S \prec^2 S'$
if and only if (i)
$S \prec^2 S'$
if and only if (i)
 $ |S| \lt |S'|$
or (ii)
$ |S| \lt |S'|$
or (ii)
 $|S|=|S'|$
and there is a bijection
$|S|=|S'|$
and there is a bijection
 $f\;:\; S \rightarrow S'$
such that:
$f\;:\; S \rightarrow S'$
such that:
 $\forall D \in S\;D \sqsubseteq f(D)$
and
$\forall D \in S\;D \sqsubseteq f(D)$
and
 $\exists D_0 \in S$
such that
$\exists D_0 \in S$
such that
 $D_0 \sqsubset f(D_0)$
.
$D_0 \sqsubset f(D_0)$
. -
 $S \prec^1 S'$
implies
$S \prec^1 S'$
implies
 $S \prec^2 S'$
but the contrary is not true in general.
$S \prec^2 S'$
but the contrary is not true in general.
3.3. An extended defnition of missing information
In this section we propose an extension of the definition of missing information we have proposed in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019):
Definition 6 Let a be an agent with its belief base
![]() $B_a$
and its goal set
$B_a$
and its goal set
![]() $G_a$
. Let
$G_a$
. Let
![]() $g \in G_a$
be such that
$g \in G_a$
be such that
![]() $B_a \not\models g$
.
$B_a \not\models g$
.
![]() $Missing(B_a,g)$
, is defined as follows:
$Missing(B_a,g)$
, is defined as follows:
![]() $Missing(B_a,g)$
is the conjunction of all the literals in the premise of g which cannot be deduced from
$Missing(B_a,g)$
is the conjunction of all the literals in the premise of g which cannot be deduced from
![]() $B_a$
(i.e., which are not yet believed by the agent). Therefore, in the particular case in which
$B_a$
(i.e., which are not yet believed by the agent). Therefore, in the particular case in which
![]() $B_a^m = \emptyset$
,
$B_a^m = \emptyset$
,
![]() $Missing(B_a,g) = premise(g)$
, that is, the missing piece of information to achieve g is premise(g).
$Missing(B_a,g) = premise(g)$
, that is, the missing piece of information to achieve g is premise(g).
The extension proposed here is based on the fact that there may be more than one way to achieve a goal instead of just one as we proposed in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019). For example, suppose you have a goal of knowing the mail address of Mr John. The different ways to achieve your goal could be to have access to his homepage or to have access to the directory of his department. This will imply to account for the usefulness of a piece of information with respect to the two possibilities to achieve the goal.
It is well known that a rule containing a disjunction, like
![]() $p \land (q \lor r) \to g$
can be decomposed into two distinct rules, like
$p \land (q \lor r) \to g$
can be decomposed into two distinct rules, like
![]() $p \land q \to g$
and
$p \land q \to g$
and
![]() $p \land r \to g$
, to be considered as being connected by a disjunction (i.e.,
$p \land r \to g$
, to be considered as being connected by a disjunction (i.e.,
![]() $(p \land q \to g) \lor (p \land r \to g)$
. However, computing the usefulness of incoming information in this case cannot be just trivially performed by computing its usefulness separately for each rule having the same goal and then combining them, for example by the maximum operator. Indeed, with the above example and assuming to already know p, if the incoming information is
$(p \land q \to g) \lor (p \land r \to g)$
. However, computing the usefulness of incoming information in this case cannot be just trivially performed by computing its usefulness separately for each rule having the same goal and then combining them, for example by the maximum operator. Indeed, with the above example and assuming to already know p, if the incoming information is
![]() $q \lor r$
, this is not enough to deduce g by either decomposed rule separately; however, it surely is enough if we consider the original (complete) rule.
$q \lor r$
, this is not enough to deduce g by either decomposed rule separately; however, it surely is enough if we consider the original (complete) rule.
The extension of Definition 6 can now be stated as follows.
Definition 7 Let a be an agent with its goal base
![]() $G_a$
and its belief base
$G_a$
and its belief base
![]() $B_a$
. Let
$B_a$
. Let
![]() $g \in G_a$
.
$g \in G_a$
.
Thus,
![]() $Missing(B_a,g)$
is a disjunction of conjunctions of literals. There are many conjunctions as premises of g. The
$Missing(B_a,g)$
is a disjunction of conjunctions of literals. There are many conjunctions as premises of g. The
![]() $k\mathrm{th}$
conjunction is the conjunction of the literals in
$k\mathrm{th}$
conjunction is the conjunction of the literals in
![]() $premise^k(g)$
which are not yet believed by a if there are some. If
$premise^k(g)$
which are not yet believed by a if there are some. If
![]() $B_a \models premise^k(g)$
Footnote 1 then this
$B_a \models premise^k(g)$
Footnote 1 then this
![]() $k\mathrm{th}$
element is any tautology, thus
$k\mathrm{th}$
element is any tautology, thus
![]() $Missing(B_a,g)$
is also any tautology and is denoted
$Missing(B_a,g)$
is also any tautology and is denoted
![]() $\top$
. This means that g is achieved, that is,
$\top$
. This means that g is achieved, that is,
![]() $B_a \models g$
. Intuitively, the
$B_a \models g$
. Intuitively, the
![]() $n_g$
premisses (conjunctions of literals) associated to goal g represent the possible ways to achieve the goal. If at least one of them is believed by the agent, it means that the goal is achieved.
$n_g$
premisses (conjunctions of literals) associated to goal g represent the possible ways to achieve the goal. If at least one of them is believed by the agent, it means that the goal is achieved.
Definition 8 Let a be an agent whose belief base is
![]() $B_a$
and goal set is
$B_a$
and goal set is
![]() $G_a = \{g_1,\ldots,g_n\}$
.
$G_a = \{g_1,\ldots,g_n\}$
.
![]() $Missing(B_a,G_a)$
is a multiset defined by:
$Missing(B_a,G_a)$
is a multiset defined by:
with
![]() $g_i \in G_a$
,
$g_i \in G_a$
,
![]() $B_a \not\models g_i$
and
$B_a \not\models g_i$
and
![]() $i \in \{1 \ldots m\}$
.
$i \in \{1 \ldots m\}$
.
Thus, the cardinality of
![]() $Missing(B_a,G_a)$
is the number of goals that are not yet achieved.
$Missing(B_a,G_a)$
is the number of goals that are not yet achieved.
Example 1 Suppose
![]() $G_a = \{g_1,g_2\}$
and
$G_a = \{g_1,g_2\}$
and
![]() $B_a^G = \{p \wedge q \rightarrow g_1, r \wedge s \rightarrow g_1, p \rightarrow g_2, r \rightarrow g_2\}$
. Suppose
$B_a^G = \{p \wedge q \rightarrow g_1, r \wedge s \rightarrow g_1, p \rightarrow g_2, r \rightarrow g_2\}$
. Suppose
![]() $B_a^W = \{p\} $
. Then,
$B_a^W = \{p\} $
. Then,
![]() $Missing(B_a,g_1)= q \vee (r \wedge s)$
,
$Missing(B_a,g_1)= q \vee (r \wedge s)$
,
![]() $Missing(B_a,g_2)= \top$
, and
$Missing(B_a,g_2)= \top$
, and
![]() $Missing(B_a,G_a)= \{q \vee (r \wedge s)\}$
. Thus,
$Missing(B_a,G_a)= \{q \vee (r \wedge s)\}$
. Thus,
![]() $g_1$
is the only goal that remains to be achieved and there are two ways to achieve it: getting q or getting r and s. Goal
$g_1$
is the only goal that remains to be achieved and there are two ways to achieve it: getting q or getting r and s. Goal
![]() $g_2$
is achieved.
$g_2$
is achieved.
The following proposition ensures that the usefulness measures we are proposing satisfy some common-sense properties, namely that (i) if some information is received, the missing information to achieve a goal cannot increase, (ii) more general information will not diminish missing information to achieve a given goal less than more specific information, and (iii) receiving a conjunction of two information items has the same effect as receiving the two items one after the other.
Proposition 1 Let
![]() $\varphi \in L$
and
$\varphi \in L$
and
![]() $g \in G_a$
.
$g \in G_a$
.
-
 $Missing(B_a \cup \varphi,g) \subseteq Missing(B_a,g)$
.
$Missing(B_a \cup \varphi,g) \subseteq Missing(B_a,g)$
. -
If
 $\psi \models \varphi$
then
$\psi \models \varphi$
then
 $Missing(B_a \cup \psi,g) \subseteq Missing(B_a \cup \varphi,g)$
.
$Missing(B_a \cup \psi,g) \subseteq Missing(B_a \cup \varphi,g)$
. -
Let
 $\varphi_1 \in L$
,
$\varphi_1 \in L$
,
 $\varphi_2 \in L$
be two formulas of L and
$\varphi_2 \in L$
be two formulas of L and
 $g \in G_a$
be a goal of agent a. We have that
$g \in G_a$
be a goal of agent a. We have that
 $Missing(B_a \cup (\varphi_1 \wedge \varphi_2), g) = Missing((B_a \cup \varphi_1) \cup \varphi_2), g)$
.
$Missing(B_a \cup (\varphi_1 \wedge \varphi_2), g) = Missing((B_a \cup \varphi_1) \cup \varphi_2), g)$
.
Proof
-
(First item)
 $Missing(B_a \cup \varphi,g)= \bigvee_{k = 1..n_g} \bigwedge_{l:\; l \in premise^k(g) \;and\; B_a \cup \varphi \not\models l} l $
. Take
$Missing(B_a \cup \varphi,g)= \bigvee_{k = 1..n_g} \bigwedge_{l:\; l \in premise^k(g) \;and\; B_a \cup \varphi \not\models l} l $
. Take
 $k \in \{1..n_g\}$
and
$k \in \{1..n_g\}$
and
 $l \in premise^k(g)$
.
$l \in premise^k(g)$
.
 $ B_a \cup \varphi \not\models l $
implies
$ B_a \cup \varphi \not\models l $
implies
 $ B_a \not\models l $
. Thus, the conjunction
$ B_a \not\models l $
. Thus, the conjunction
 $ \bigwedge_{l:\; l \in premise^k(g) \;and\; B_a \cup \varphi \not\models l} l $
is included in
$ \bigwedge_{l:\; l \in premise^k(g) \;and\; B_a \cup \varphi \not\models l} l $
is included in
 $ \bigwedge_{l:\; l \in premise^k(g) \;and\; B_a \not\models l} l $
. This proves
$ \bigwedge_{l:\; l \in premise^k(g) \;and\; B_a \not\models l} l $
. This proves
 $Missing(B_a \cup \varphi,g) \subseteq Missing(B_a,g)$
.
$Missing(B_a \cup \varphi,g) \subseteq Missing(B_a,g)$
. -
(Second item) Consider the
 $k\mathrm{th}$
conjunction of
$k\mathrm{th}$
conjunction of
 $Missing(B_a \cup \psi,g)$
that is
$Missing(B_a \cup \psi,g)$
that is $\bigwedge_{l:\; l \in premise^k(g) \;and\; B_a \cup \psi \not\models l} l $
. If
$\bigwedge_{l:\; l \in premise^k(g) \;and\; B_a \cup \psi \not\models l} l $
. If
 $\psi \models \varphi$
then
$\psi \models \varphi$
then
 $B_a \cup \psi \not\models l$
implies
$B_a \cup \psi \not\models l$
implies
 $B_a \cup \varphi \not\models l$
. Thus, the
$B_a \cup \varphi \not\models l$
. Thus, the
 $k\mathrm{th}$
conjunction of
$k\mathrm{th}$
conjunction of
 $Missing(B_a \cup \psi,g$
is included in the
$Missing(B_a \cup \psi,g$
is included in the
 $k\mathrm{th}$
conjunction of
$k\mathrm{th}$
conjunction of
 $Missing(B_a \cup \varphi,g$
. This proves that
$Missing(B_a \cup \varphi,g$
. This proves that
 $Missing(B_a \cup \psi,g) \subseteq Missing(B_a \cup \varphi,g)$
.
$Missing(B_a \cup \psi,g) \subseteq Missing(B_a \cup \varphi,g)$
. -
(Third item) The proof is similar to the previous one. We just have to notice that
 $B_a \cup (\varphi_1 \wedge \varphi_2),g \not \models l$
if and only if
$B_a \cup (\varphi_1 \wedge \varphi_2),g \not \models l$
if and only if
 $(B_a \cup \varphi_1) \cup \varphi_2),g \not \models l$
.
$(B_a \cup \varphi_1) \cup \varphi_2),g \not \models l$
.
Example 2 Let us consider a propositional language whose letters are p, q, r, s,
![]() $g_1$
, and
$g_1$
, and
![]() $g_2$
, respectively, meaning ‘I know the main papers about modal logic’, ‘I know the main papers about BDI agents’, ‘I know Python’, ‘I know SQL’, ‘I can write my paper’ and ‘I can prepare my Monday’s class’. Let us consider
$g_2$
, respectively, meaning ‘I know the main papers about modal logic’, ‘I know the main papers about BDI agents’, ‘I know Python’, ‘I know SQL’, ‘I can write my paper’ and ‘I can prepare my Monday’s class’. Let us consider
![]() $G_a = \{g_1, g_2\}$
and
$G_a = \{g_1, g_2\}$
and
![]() $B_a^W = \{p\}$
. Suppose
$B_a^W = \{p\}$
. Suppose
![]() $B_a^G = \{ p \wedge q \rightarrow g_1, r \rightarrow g_2, s \rightarrow g_2\}$
. Then
$B_a^G = \{ p \wedge q \rightarrow g_1, r \rightarrow g_2, s \rightarrow g_2\}$
. Then
![]() $Missing(B_a, G_a) = \{q, r \vee s\}$
. This means that, in order to achieve its two goals, the agent lacks knowledge about BDI agents and about Python or SQL.
$Missing(B_a, G_a) = \{q, r \vee s\}$
. This means that, in order to achieve its two goals, the agent lacks knowledge about BDI agents and about Python or SQL.
The following proposition shows that adding a belief to the belief base
![]() $B_a$
does not increase the number of goals that remain to be achieved. Finally, if adding a belief to the belief base
$B_a$
does not increase the number of goals that remain to be achieved. Finally, if adding a belief to the belief base
![]() $B_a$
reduces the number of missing conjunctions, then this means that such new belief allows to achieve one or more goals.
$B_a$
reduces the number of missing conjunctions, then this means that such new belief allows to achieve one or more goals.
Proposition 2 Let
![]() $\varphi \in L$
.
$\varphi \in L$
.
-
 $|Missing(B_a \cup \varphi,G_a)| \leq |Missing(B_a, G_a)|$
.
$|Missing(B_a \cup \varphi,G_a)| \leq |Missing(B_a, G_a)|$
. -
If
 $|Missing(B_a \cup \varphi,G_a)| \lt |Missing(B_a, G_a)|$
then
$|Missing(B_a \cup \varphi,G_a)| \lt |Missing(B_a, G_a)|$
then
 $\exists g_i \in G_a$
such that
$\exists g_i \in G_a$
such that
 $Missing(B_a,g_i) \in Missing(B_a, G_a)$
and
$Missing(B_a,g_i) \in Missing(B_a, G_a)$
and
 $B_a \cup \varphi \models g_i$
.
$B_a \cup \varphi \models g_i$
.
Proof
-
(First item) Let
 $g \in G_a$
.
$g \in G_a$
.
 $B_a \cup \varphi \not\models g$
implies
$B_a \cup \varphi \not\models g$
implies
 $B_a \not\models g$
. Thus,
$B_a \not\models g$
. Thus,
 $\{g\;:\; g \in G_a\;st\;B_a \cup \varphi \not\models g\} \subseteq \{g\;:\; g \in G_a\;st\;B_a \not\models g\}$
. Thus,
$\{g\;:\; g \in G_a\;st\;B_a \cup \varphi \not\models g\} \subseteq \{g\;:\; g \in G_a\;st\;B_a \not\models g\}$
. Thus,
 $\mid \{g\;:\; g \in G_a\;st\;B_a \cup \varphi \not\models g\} \mid \leq \mid \{g\;:\; g \in G_a\;st\;B_a \not\models g\} \mid$
. Finally,
$\mid \{g\;:\; g \in G_a\;st\;B_a \cup \varphi \not\models g\} \mid \leq \mid \{g\;:\; g \in G_a\;st\;B_a \not\models g\} \mid$
. Finally,
 $|Missing(B_a \cup \varphi,G_a)| \leq |Missing(B_a, G_a)|$
.
$|Missing(B_a \cup \varphi,G_a)| \leq |Missing(B_a, G_a)|$
. -
(Second item)) Suppose that
 $|Missing(B_a \cup \varphi,G_a)| \lt |Missing(B_a, G_a)|$
. Thus,
$|Missing(B_a \cup \varphi,G_a)| \lt |Missing(B_a, G_a)|$
. Thus,
 $\mid \{g\;:\; g \in G_a\;st\;B_a \cup \varphi \not\models g\}\mid \lt \mid \{g\;:\; g \in G_a\;st\;B_a \not\models g\} \mid$
. But since,
$\mid \{g\;:\; g \in G_a\;st\;B_a \cup \varphi \not\models g\}\mid \lt \mid \{g\;:\; g \in G_a\;st\;B_a \not\models g\} \mid$
. But since,
 $\{g\;:\; g \in G_a\;st\;B_a \cup \varphi \not\models g\} \subseteq \{g\;:\; g \in G_a\;st\;B_a \not\models g\}$
, this means that
$\{g\;:\; g \in G_a\;st\;B_a \cup \varphi \not\models g\} \subseteq \{g\;:\; g \in G_a\;st\;B_a \not\models g\}$
, this means that
 $\exists g \in G_a$
such that
$\exists g \in G_a$
such that
 $B_a \not\models g$
and
$B_a \not\models g$
and
 $B_a \cup \varphi \models g$
. That is,
$B_a \cup \varphi \models g$
. That is,
 $\exists g \in G_a$
st
$\exists g \in G_a$
st
 $Missing(B_a,g) \in Missing(B_a,G_a)$
and
$Missing(B_a,g) \in Missing(B_a,G_a)$
and
 $B_a \cup \varphi \models g$
.
$B_a \cup \varphi \models g$
.
Notice however that, even if
![]() $|Missing(B_a \cup \varphi,G_a)| \leq |Missing(B_a, G_a)|$
, it may happen that
$|Missing(B_a \cup \varphi,G_a)| \leq |Missing(B_a, G_a)|$
, it may happen that
![]() $Missing(B_a \cup \varphi,G_a) \not\subseteq Missing(B_a, G_a)$
. See example below.
$Missing(B_a \cup \varphi,G_a) \not\subseteq Missing(B_a, G_a)$
. See example below.
Example 3 Consider
![]() $G_a = \{g_1,g_2\}$
,
$G_a = \{g_1,g_2\}$
,
![]() $B_a^W = \emptyset$
and
$B_a^W = \emptyset$
and
![]() $B_a^G = \{ p \wedge q \rightarrow g_1, r \rightarrow g_2, s \rightarrow g_2\}$
. Then
$B_a^G = \{ p \wedge q \rightarrow g_1, r \rightarrow g_2, s \rightarrow g_2\}$
. Then
![]() $Missing(B_a, G_a) = \{p \wedge q, r \vee s\}$
, that is none of the two goals is achieved: to achieve
$Missing(B_a, G_a) = \{p \wedge q, r \vee s\}$
, that is none of the two goals is achieved: to achieve
![]() $g_1$
,
$g_1$
,
![]() $p \wedge q$
must be believed and to achieve
$p \wedge q$
must be believed and to achieve
![]() $g_2$
, r or s must be believed.
$g_2$
, r or s must be believed.
![]() $Missing(B_a \cup p, G_a) = \{q, r \vee s\}$
. The two goals remain to be achieved but now, only q is missing to achieve
$Missing(B_a \cup p, G_a) = \{q, r \vee s\}$
. The two goals remain to be achieved but now, only q is missing to achieve
![]() $g_1$
. Finally,
$g_1$
. Finally,
![]() $Missing(B_a \cup r, G_a) = \{p \wedge q\}$
. Here,
$Missing(B_a \cup r, G_a) = \{p \wedge q\}$
. Here,
![]() $g_2$
is achieved that is
$g_2$
is achieved that is
![]() $B_a \cup r \models g_2$
.
$B_a \cup r \models g_2$
.
As we have pointed out in Section 2, the aim of traditional IR systems is to provide to the user a list of documents that best fit with the user query. The proposed documents are then ranked with respect to the aboutness measure, which, roughly speaking, represents the degree of matching between the document and the user query. However, such a measure does not consider what the user already knows, nor their informative goals; as a consequence, it does not necessarily help providing documents that make the user knowledge advance toward their goals.
In the following three sections, we propose three different measures, of increasing refinement, allowing a system to evaluate the usefulness of a piece of information to the user (given the beliefs about the user goals and about the current user knowledge), in various ways: the first one is binary, in that it just tells whether a piece of information is useful or not; the second one allows to compare two pieces of information and decide if one of them is more useful than the other; finally, the third measure assigns a numerical value of information usefulness to a given piece of information, which, in addition to telling if one piece of information is more useful that another, also quantifies by how much.
4. A binary approach
In this section, we extend the binary definition of the usefulness measure proposed in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019). We characterize useful information for an agent in view of achieving (or getting closer to), at least one of its goals in two different ways. According to this binary approach, a piece of information is either useful or not.
Definition 9 Let a be an agent with its belief base
![]() $B_a$
and its set of goals
$B_a$
and its set of goals
![]() $G_a$
. Let
$G_a$
. Let
![]() $\varphi \in L$
.
$\varphi \in L$
.
![]() $\varphi$
is
$\varphi$
is
![]() $U^1$
-useful for agent a if and only if
$U^1$
-useful for agent a if and only if
![]() $ Missing(B_a \cup \varphi, G_a) \prec^1 Missing(B_a,G_a)$
. We use the notation
$ Missing(B_a \cup \varphi, G_a) \prec^1 Missing(B_a,G_a)$
. We use the notation
![]() $U_{G_a,B_a}^1 \varphi$
or, more simply,
$U_{G_a,B_a}^1 \varphi$
or, more simply,
![]() $U^1 \varphi$
, when there is no ambiguity.
$U^1 \varphi$
, when there is no ambiguity.
According to this definition, a formula
![]() $\varphi$
in L is useful for a in view of achieving its goals
$\varphi$
in L is useful for a in view of achieving its goals
![]() $G_a$
if and only if being aware of
$G_a$
if and only if being aware of
![]() $\varphi$
will allow a to achieve a goal or to reduce (by inclusion) missing information.
$\varphi$
will allow a to achieve a goal or to reduce (by inclusion) missing information.
Example 4 Take Example 3 with
![]() $G_a = \{g_1,g_2\}$
,
$G_a = \{g_1,g_2\}$
,
![]() $B_a^W = \emptyset$
and
$B_a^W = \emptyset$
and
![]() $B_a^G = \{ p \wedge q \rightarrow g_1, r \rightarrow g_2, s \rightarrow g_2\}$
. We have shown that
$B_a^G = \{ p \wedge q \rightarrow g_1, r \rightarrow g_2, s \rightarrow g_2\}$
. We have shown that
![]() $Missing(B_a, G_a) = \{p \wedge q, r \vee s\}$
. And we have
$Missing(B_a, G_a) = \{p \wedge q, r \vee s\}$
. And we have
![]() $Missing(B_a \cup p, G_a) = \{q, r \vee s\}$
and
$Missing(B_a \cup p, G_a) = \{q, r \vee s\}$
and
![]() $Missing(B_a \cup r, G_a) = \{p \wedge q\}$
. Notice that
$Missing(B_a \cup r, G_a) = \{p \wedge q\}$
. Notice that
![]() $\{q, r \vee s\} \prec^1 \{p \wedge q, r \vee s\}$
since
$\{q, r \vee s\} \prec^1 \{p \wedge q, r \vee s\}$
since
![]() $q \subset p \wedge q$
. Thus, p is
$q \subset p \wedge q$
. Thus, p is
![]() $U^1$
-useful for agent a : even if getting p does not help a to achieve a goal, it helps it to reduce missing information. Besides,
$U^1$
-useful for agent a : even if getting p does not help a to achieve a goal, it helps it to reduce missing information. Besides,
![]() $\{p \wedge q\} \prec^1 \{p \wedge q, r \vee s\}$
since the set
$\{p \wedge q\} \prec^1 \{p \wedge q, r \vee s\}$
since the set
![]() $\{p \wedge q\}$
is smaller that
$\{p \wedge q\}$
is smaller that
![]() $ \{p \wedge q, r \vee s\}$
. Thus, r is
$ \{p \wedge q, r \vee s\}$
. Thus, r is
![]() $U^1$
-useful for agent a because getting r helps a to achieve one of its goals.
$U^1$
-useful for agent a because getting r helps a to achieve one of its goals.
Definition 10 Let a be an agent with its belief base
![]() $B_a$
and its goals
$B_a$
and its goals
![]() $G_a$
. Let
$G_a$
. Let
![]() $\varphi \in L$
.
$\varphi \in L$
.
![]() $\varphi$
is
$\varphi$
is
![]() $U^2$
-useful for a if and only if
$U^2$
-useful for a if and only if
![]() $Missing(B_a \cup \varphi, G_a) \prec^2 Missing(B_a,G_a)$
. We use the notation
$Missing(B_a \cup \varphi, G_a) \prec^2 Missing(B_a,G_a)$
. We use the notation
![]() $U_{G_a,B_a}^2 \varphi$
or
$U_{G_a,B_a}^2 \varphi$
or
![]() $U^2 \varphi$
when there is no ambiguity.
$U^2 \varphi$
when there is no ambiguity.
According to this second definition, a formula
![]() $\varphi$
of L is
$\varphi$
of L is
![]() $U^2$
-useful for a if knowing
$U^2$
-useful for a if knowing
![]() $\varphi$
allows a to achieve one goal or to reduce (by cardinality) its missing information.
$\varphi$
allows a to achieve one goal or to reduce (by cardinality) its missing information.
The following proposition shows that the two previous definitions, based on two different preorders, are equivalent. What this means is that providing the user with a piece of information which is part of the missing information also decreases the cardinality of missing information, and vice versa.
Proposition 3
![]() $U^1 \varphi \;\Longleftrightarrow U^2 \varphi$
.
$U^1 \varphi \;\Longleftrightarrow U^2 \varphi$
.
Proof
-
In Section 3.2, we have noticed that
 $S \prec^1 S'$
implies
$S \prec^1 S'$
implies
 $S \preceq^2 S'$
. Thus,
$S \preceq^2 S'$
. Thus,
 $Missing(B_a \cup \varphi,G_a) \prec^1 Missing(B_a,G_a)$
implies
$Missing(B_a \cup \varphi,G_a) \prec^1 Missing(B_a,G_a)$
implies
 $Missing(B_a \cup \varphi,G_a) \prec^2 Missing(B_a,G_a)$
. Thus finally,
$Missing(B_a \cup \varphi,G_a) \prec^2 Missing(B_a,G_a)$
. Thus finally,
 $U^1 \varphi \;\Longrightarrow U^2 \varphi$
.
$U^1 \varphi \;\Longrightarrow U^2 \varphi$
. -
Let us now show
 $U^2 \varphi \;\Longrightarrow U^1 \varphi$
.
$U^2 \varphi \;\Longrightarrow U^1 \varphi$
.
 $U^2 \varphi$
if and only if
$U^2 \varphi$
if and only if
 $Missing(B_a \cup \varphi,G_a) \prec^2 Missing(B_a,G_a)$
. Thus, (i)
$Missing(B_a \cup \varphi,G_a) \prec^2 Missing(B_a,G_a)$
. Thus, (i)
 $\mid Missing(B_a \cup \varphi,G_a)\mid \lt \mid Missing(B_a,G_a) \mid $
or (ii)
$\mid Missing(B_a \cup \varphi,G_a)\mid \lt \mid Missing(B_a,G_a) \mid $
or (ii)
 $\mid Missing(B_a \cup \varphi,G_a)\mid = \mid Missing(B_a,G_a) \mid $
and there is a bijection
$\mid Missing(B_a \cup \varphi,G_a)\mid = \mid Missing(B_a,G_a) \mid $
and there is a bijection
 $f\;:\; Missing(B_a \cup \varphi,G_a) \rightarrow Missing(B_a,G_a)$
such that
$f\;:\; Missing(B_a \cup \varphi,G_a) \rightarrow Missing(B_a,G_a)$
such that
 $\forall D \in Missing(B_a \cup \varphi,G_a),D \sqsubseteq f(D)$
and
$\forall D \in Missing(B_a \cup \varphi,G_a),D \sqsubseteq f(D)$
and
 $\exists D_o \in Missing(B_a \cup \varphi,G_a)$
such that
$\exists D_o \in Missing(B_a \cup \varphi,G_a)$
such that
 $D_0 \sqsubset f(D_0)$
. Thus,
$D_0 \sqsubset f(D_0)$
. Thus,
 $\exists C_0 \in D_0$
$\exists C_0 \in D_0$
 $\forall C' \in f(D_0)$
$\forall C' \in f(D_0)$
 $\mid C_0\mid \lt \mid C'\mid$
.
$\mid C_0\mid \lt \mid C'\mid$
.-
– If (i) is true then
 $Missing(B_a \cup \varphi,G_a) \prec^1 Missing(B_a,G_a)$
thus finally
$Missing(B_a \cup \varphi,G_a) \prec^1 Missing(B_a,G_a)$
thus finally
 $U^1 \varphi$
.
$U^1 \varphi$
. -
– If (ii) is true, then by the second item of Proposition 2, we conclude that
 $\forall D \in Missing(B_a \cup \varphi,G_a), D \subseteq f(D)$
.
$\forall D \in Missing(B_a \cup \varphi,G_a), D \subseteq f(D)$
.Take
 $D_0$
. Since
$D_0$
. Since
 $D_0 \subseteq f(D_0)$
we have:
$D_0 \subseteq f(D_0)$
we have:
 $\forall C \in D_0\; \exists C' \in f(D_0) \;st\; C \subseteq C'$
. Take
$\forall C \in D_0\; \exists C' \in f(D_0) \;st\; C \subseteq C'$
. Take
 $C_0$
. We have
$C_0$
. We have
 $\exists C'_{\!\!0} \in f(D_0) \;st\; C_0 \subseteq C'_{\!\!0}$
. and
$\exists C'_{\!\!0} \in f(D_0) \;st\; C_0 \subseteq C'_{\!\!0}$
. and
 $\forall C' \in f(D_0)$
$\forall C' \in f(D_0)$
 $\mid C_0 \mid \lt \mid C'\mid$
. Thus,
$\mid C_0 \mid \lt \mid C'\mid$
. Thus,
 $\exists C'_{\!\!0} \in f(D_0) \;st\; C_0 \subset C'_{\!\!0}$
. Thus,
$\exists C'_{\!\!0} \in f(D_0) \;st\; C_0 \subset C'_{\!\!0}$
. Thus,
 $D_0 \subset f(D_0)$
.
$D_0 \subset f(D_0)$
.Finally,
 $\forall D \in Missing(B_a \cup \varphi,G_a), D \subseteq f(D)$
and
$\forall D \in Missing(B_a \cup \varphi,G_a), D \subseteq f(D)$
and
 $\exists D_0 \in Missing(B_a \cup \varphi,G_a) \;st\; D_0 \subset f(D_0)$
. That is,
$\exists D_0 \in Missing(B_a \cup \varphi,G_a) \;st\; D_0 \subset f(D_0)$
. That is,
 $Missing(B_a \cup \varphi,G_a) \prec^1 Missing(B_a \varphi,G_a)$
. Thus,
$Missing(B_a \cup \varphi,G_a) \prec^1 Missing(B_a \varphi,G_a)$
. Thus,
 $U^1 \varphi$
.
$U^1 \varphi$
.
-
Since
![]() $U^1 \varphi$
and
$U^1 \varphi$
and
![]() $U^2 \varphi$
are equivalent, we will use just
$U^2 \varphi$
are equivalent, we will use just
![]() $U \varphi$
to denote both.
$U \varphi$
to denote both.
Example 5 Consider Example 2 again.
![]() $Missing(B_a,G_a) = \{q, r \vee s\}$
.
$Missing(B_a,G_a) = \{q, r \vee s\}$
.
![]() $Missing(B_a \cup \{r\}, G_a) = \{q\}$
.
$Missing(B_a \cup \{r\}, G_a) = \{q\}$
.
![]() $Missing(B_a \cup \{q\}, G_a) = \{r \vee s\}$
.
$Missing(B_a \cup \{q\}, G_a) = \{r \vee s\}$
.
![]() $Missing(B_a \cup \{q \wedge r\}, G_a) = \emptyset$
. Therefore, U r, U q, and
$Missing(B_a \cup \{q \wedge r\}, G_a) = \emptyset$
. Therefore, U r, U q, and
![]() $U (q \wedge r)$
.
$U (q \wedge r)$
.
Finally, let us show a weakness of this binary model by illustrating it on the previous example. We can show that if x is a propositional letter,
![]() $r \wedge x$
is also useful. Indeed, knowing Python and Java is useful for the agent because it allows the agent to achieve
$r \wedge x$
is also useful. Indeed, knowing Python and Java is useful for the agent because it allows the agent to achieve
![]() $g_2$
. But this could be questionable because reading a document on Python and Java, certainly allows the agent to acquire useful information about Python to prepare the class, but leads the agent to read content about Java, not useful for achieving its goals. This limitation is formally emphasized by the following proposition.
$g_2$
. But this could be questionable because reading a document on Python and Java, certainly allows the agent to acquire useful information about Python to prepare the class, but leads the agent to read content about Java, not useful for achieving its goals. This limitation is formally emphasized by the following proposition.
Proposition 4 Let
![]() $\varphi_1$
and
$\varphi_1$
and
![]() $\varphi_2$
be two formulas of L such that
$\varphi_2$
be two formulas of L such that
![]() $\varphi_2 \models \varphi_1$
. Then,
$\varphi_2 \models \varphi_1$
. Then,
Proof First notice that because
![]() $\varphi_2 \models \varphi_1$
we have
$\varphi_2 \models \varphi_1$
we have
![]() $\forall g \in G_a\; Missing(B_a \cup \varphi_2,g) \subseteq Missing(B_a \cup \varphi_1,g)$
(see Proposition 1) thus
$\forall g \in G_a\; Missing(B_a \cup \varphi_2,g) \subseteq Missing(B_a \cup \varphi_1,g)$
(see Proposition 1) thus
![]() $Missing(B_a \cup \varphi_2,G_a) \subseteq Missing(B_a \cup \varphi_1,G_a)$
. Finally,
$Missing(B_a \cup \varphi_2,G_a) \subseteq Missing(B_a \cup \varphi_1,G_a)$
. Finally,
![]() $\mid Missing(B_a \cup \varphi_2,G_a)\mid \leq \mid Missing(B_a \cup \varphi_1,G_a)\mid$
.
$\mid Missing(B_a \cup \varphi_2,G_a)\mid \leq \mid Missing(B_a \cup \varphi_1,G_a)\mid$
.
Suppose
![]() $U \varphi_1$
that is,
$U \varphi_1$
that is,
![]() $Missing(B_a \cup \varphi_1,G_a) \prec^1 Missing(B_a,G_a)$
$Missing(B_a \cup \varphi_1,G_a) \prec^1 Missing(B_a,G_a)$
-
Suppose
 $\mid Missing(B_a \cup \varphi_1,G_a)\mid \lt \mid Missing(B_a,G_a) \mid $
. Then, by the previous remark we conclude
$\mid Missing(B_a \cup \varphi_1,G_a)\mid \lt \mid Missing(B_a,G_a) \mid $
. Then, by the previous remark we conclude
 $\mid Missing(B_a \cup \varphi_2,G_a)\mid \lt \mid Missing(B_a,G_a) \mid $
and finally
$\mid Missing(B_a \cup \varphi_2,G_a)\mid \lt \mid Missing(B_a,G_a) \mid $
and finally
 $U \varphi_2$
.
$U \varphi_2$
. -
Suppose now that
 $\mid Missing(B_a \cup \varphi_1,G_a)\mid = \mid Missing(B_a,G_a) \mid $
and
$\mid Missing(B_a \cup \varphi_1,G_a)\mid = \mid Missing(B_a,G_a) \mid $
and
 $\exists f\;:\; Missing(B_a \cup \varphi_1,G_a) \rightarrow Missing(B_a,G_a)$
st
$\exists f\;:\; Missing(B_a \cup \varphi_1,G_a) \rightarrow Missing(B_a,G_a)$
st
 $\forall D \in Missing(B_a \cup \varphi_1,G_a) D \subseteq f(D) \;and\; \exists D_0 \in Missing(B_a \cup \varphi_1,G_a)\;D_0 \subset f(D_0)$
.
$\forall D \in Missing(B_a \cup \varphi_1,G_a) D \subseteq f(D) \;and\; \exists D_0 \in Missing(B_a \cup \varphi_1,G_a)\;D_0 \subset f(D_0)$
.-
– If
 $\mid Missing(B_a \cup \varphi_2,G_a)\mid \lt \mid Missing(B_a \cup \varphi_1,G_a)\mid$
then
$\mid Missing(B_a \cup \varphi_2,G_a)\mid \lt \mid Missing(B_a \cup \varphi_1,G_a)\mid$
then
 $\mid Missing(B_a \cup \varphi_2,G_a)\mid \lt \mid Missing(B_a,G_a)\mid$
thus finally
$\mid Missing(B_a \cup \varphi_2,G_a)\mid \lt \mid Missing(B_a,G_a)\mid$
thus finally
 $U \varphi_2$
.
$U \varphi_2$
. -
– If
 $\mid Missing(B_a \cup \varphi_2,G_a)\mid = \mid Missing(B_a \cup \varphi_1,G_a)\mid$
then
$\mid Missing(B_a \cup \varphi_2,G_a)\mid = \mid Missing(B_a \cup \varphi_1,G_a)\mid$
then
 $\mid Missing(B_a \cup \varphi_2,G_a)\mid = \mid Missing(B_a,G_a)\mid$
.
$\mid Missing(B_a \cup \varphi_2,G_a)\mid = \mid Missing(B_a,G_a)\mid$
.Moreover, since
 $Missing(B_a \cup \varphi_2,G_a) \subseteq Missing(B_a \cup \varphi_1,G_a)$
, we can consider the restriction of function f to
$Missing(B_a \cup \varphi_2,G_a) \subseteq Missing(B_a \cup \varphi_1,G_a)$
, we can consider the restriction of function f to
 $Missing(B_a \cup \varphi_2)$
. Thus,
$Missing(B_a \cup \varphi_2)$
. Thus,
 $\forall D \in Missing(B_a \cup \varphi_2,G_a)\;D \subseteq f(D)$
.
$\forall D \in Missing(B_a \cup \varphi_2,G_a)\;D \subseteq f(D)$
.Consider
 $D_0$
.
$D_0$
.
 $\exists g_0 \in G_a$
st
$\exists g_0 \in G_a$
st
 $D_0 = Missing(B_a \cup \varphi_1,g_0)$
. We thus have
$D_0 = Missing(B_a \cup \varphi_1,g_0)$
. We thus have
 $Missing(B_a \cup \varphi_2,g_0) \subseteq D_0$
. Finally
$Missing(B_a \cup \varphi_2,g_0) \subseteq D_0$
. Finally
 $\exists D'_{\!\!0} = Missing(B_a \cup \varphi_2,g_0)\;st\; D'_{\!\!0} \subset f(D'0)$
. Finally
$\exists D'_{\!\!0} = Missing(B_a \cup \varphi_2,g_0)\;st\; D'_{\!\!0} \subset f(D'0)$
. Finally
 $U \varphi_2$
.
$U \varphi_2$
.
-
The following proposition ensures that some more common-sense properties are satisfied by our proposed measures: (i) acquiring a useless piece of information does not modify the missing information, (ii) any piece of information which allows one to deduce a useful piece of information is also useful, (iii) a piece of information may be useful only in part and therefore may not be one of the elements in the missing information set, (iv) anything that can be derived from useful information is not necessarily useful in itself.
Proposition 5
-
If
 $\varphi$
is not useful then
$\varphi$
is not useful then
 $Missing(B_a \cup \varphi, G_a) = Missing(B_a, G_a)$
.
$Missing(B_a \cup \varphi, G_a) = Missing(B_a, G_a)$
. -
If
 $\exists D \in Missing(B_a,G_a)$
such that
$\exists D \in Missing(B_a,G_a)$
such that
 $\varphi \models D$
then
$\varphi \models D$
then
 $U \varphi$
.
$U \varphi$
. -
But
 $\ U \varphi $
does not imply
$\ U \varphi $
does not imply
 $\exists D \in Missing(B_a,G_a)\;such that\; \varphi \models D$
.
$\exists D \in Missing(B_a,G_a)\;such that\; \varphi \models D$
. -
Even if
 $ \exists D \in Missing(B_a,G_a)\;st\; D \models \varphi$
, it may happen that
$ \exists D \in Missing(B_a,G_a)\;st\; D \models \varphi$
, it may happen that
 $\varphi $
is not useful.
$\varphi $
is not useful.
Proof
-
(First item) If
 $\varphi$
is not useful then
$\varphi$
is not useful then
 $Missing(B_a \cup \varphi, G_a) \not\prec^1 Missing(B_a,G_a)$
. Thus,
$Missing(B_a \cup \varphi, G_a) \not\prec^1 Missing(B_a,G_a)$
. Thus,
 $\mid Missing(B_a \cup \varphi, G_a) \mid \geq \mid Missing(B_a,G_a) \mid$
and if
$\mid Missing(B_a \cup \varphi, G_a) \mid \geq \mid Missing(B_a,G_a) \mid$
and if
 $\mid Missing(B_a \cup \varphi, G_a) \mid = \mid Missing(B_a,G_a) \mid$
then
$\mid Missing(B_a \cup \varphi, G_a) \mid = \mid Missing(B_a,G_a) \mid$
then
 $\forall f \ bijection\;:\; Missing(B_a \cup \varphi, G_a) \rightarrow Missing(B_a,G_a)$
,
$\forall f \ bijection\;:\; Missing(B_a \cup \varphi, G_a) \rightarrow Missing(B_a,G_a)$
,
 $\exists D \in Missing(B_a \cup \varphi, G_a) \;st \ D \not\subseteq f(D) $
or
$\exists D \in Missing(B_a \cup \varphi, G_a) \;st \ D \not\subseteq f(D) $
or
 $\forall D \in Missing(B_a \cup \varphi, G_a) D \not\subset f(D)$
.
$\forall D \in Missing(B_a \cup \varphi, G_a) D \not\subset f(D)$
.Since
 $\mid Missing(B_a \cup \varphi, G_a) \mid \leq \mid Missing(B_a,G_a) \mid$
we conclude
$\mid Missing(B_a \cup \varphi, G_a) \mid \leq \mid Missing(B_a,G_a) \mid$
we conclude
 $\mid Missing(B_a \cup \varphi, G_a) \mid = \mid Missing(B_a,G_a) \mid$
and then
$\mid Missing(B_a \cup \varphi, G_a) \mid = \mid Missing(B_a,G_a) \mid$
and then
 $\forall f bijection\;:\; Missing(B_a \cup \varphi, G_a) \rightarrow Missing(B_a,G_a)$
,
$\forall f bijection\;:\; Missing(B_a \cup \varphi, G_a) \rightarrow Missing(B_a,G_a)$
,
 $\exists D \in Missing(B_a \cup \varphi, G_a)) \;st \ D \not\subseteq f(D) $
or
$\exists D \in Missing(B_a \cup \varphi, G_a)) \;st \ D \not\subseteq f(D) $
or
 $\forall D \in Missing(B_a \cup \varphi, G_a) D \not\subset f(D)$
.
$\forall D \in Missing(B_a \cup \varphi, G_a) D \not\subset f(D)$
.Consider the bijection f defined by
 $f(Missing(B_a\cup \varphi,g)) = Missing(B_a,g)$
for any
$f(Missing(B_a\cup \varphi,g)) = Missing(B_a,g)$
for any
 $g \in G_a$
By Proposition 1, we have
$g \in G_a$
By Proposition 1, we have
 $\forall g \in G_a\;Missing(B_a\cup \varphi,g) \subseteq Missing(B_a,g)$
; thus, we cannot have
$\forall g \in G_a\;Missing(B_a\cup \varphi,g) \subseteq Missing(B_a,g)$
; thus, we cannot have
 $\exists D \in Missing(B_a \cup \varphi, g) \;st D \not\subseteq f(D) $
. Thus, we have
$\exists D \in Missing(B_a \cup \varphi, g) \;st D \not\subseteq f(D) $
. Thus, we have
 $\forall D \in Missing(B_a \cup \varphi, g) D \not\subset f(D)$
. Thus
$\forall D \in Missing(B_a \cup \varphi, g) D \not\subset f(D)$
. Thus
 $\forall g \in G_a \;Missing(B_a \cup \varphi,g) D \not\subset Missing(B_a,g)$
. Consequently,
$\forall g \in G_a \;Missing(B_a \cup \varphi,g) D \not\subset Missing(B_a,g)$
. Consequently,
 $\forall g \in G_a \;Missing(B_a \cup \varphi,g)= Missing(B_a,g)$
. Finally,
$\forall g \in G_a \;Missing(B_a \cup \varphi,g)= Missing(B_a,g)$
. Finally,
 $Missing(B_a \cup \varphi,G_a) = Missing(B_a,G_a)$
.
$Missing(B_a \cup \varphi,G_a) = Missing(B_a,G_a)$
. -
(Second item) First notice that
 $\forall D \in Missing(B_a,G_a)$
, U D. Indeed, if
$\forall D \in Missing(B_a,G_a)$
, U D. Indeed, if
 $D \in Missing(B_a,G_a)$
, there exists
$D \in Missing(B_a,G_a)$
, there exists
 $g \in G_a$
st
$g \in G_a$
st
 $B_a \not\models g$
and
$B_a \not\models g$
and
 $D = Missing(B_a,g)$
and
$D = Missing(B_a,g)$
and
 $B_a \cup D \models g$
. Thus finally,
$B_a \cup D \models g$
. Thus finally,
 $Missing(B_a \cup D,G_a) \prec^1Missing(B_a,G_a)$
that is, U D.
$Missing(B_a \cup D,G_a) \prec^1Missing(B_a,G_a)$
that is, U D.Take
 $\varphi$
and suppose
$\varphi$
and suppose
 $\exists D \in Missing(B_a,G_a)$
such that
$\exists D \in Missing(B_a,G_a)$
such that
 $\varphi \models D$
. Thus, by Proposition 4 we conclude
$\varphi \models D$
. Thus, by Proposition 4 we conclude
 $U \varphi$
.
$U \varphi$
. -
(Third item) Consider Example 1. We have shown
 $Missing(B_a,G_a) = \{q \vee (r \wedge s)\}$
. We can show that U r, but
$Missing(B_a,G_a) = \{q \vee (r \wedge s)\}$
. We can show that U r, but
 $ r \not\models q \vee (r \wedge s)$
.
$ r \not\models q \vee (r \wedge s)$
. -
(Fourth item). Consider Example 5 and
 $\varphi = q \vee x$
.
$\varphi = q \vee x$
.
 $q \in Missing(B_a,G_a)$
and
$q \in Missing(B_a,G_a)$
and
 $q \models q \vee x$
but
$q \models q \vee x$
but
 $q \vee x$
is not useful.
$q \vee x$
is not useful.
5. An ordinal approach
In this section we are interested in a notion of relative usefulness by defining, in two different ways, a preorder between the formulas. To compare two formulas
![]() $\varphi_1$
and
$\varphi_1$
and
![]() $\varphi_2$
, we compare the two sets of information that is missing once the piece of information is added to the belief base, that is, we compare
$\varphi_2$
, we compare the two sets of information that is missing once the piece of information is added to the belief base, that is, we compare
![]() $Missing(B_a \cup \varphi_1,G_a)$
and
$Missing(B_a \cup \varphi_1,G_a)$
and
![]() $Missing(B_a \cup \varphi_2,G_a)$
, by using either of the preorders
$Missing(B_a \cup \varphi_2,G_a)$
, by using either of the preorders
![]() $\preceq^1$
and
$\preceq^1$
and
![]() $\preceq^2$
. Here, the obtained definitions will not be equivalent (see Example 6 below).
$\preceq^2$
. Here, the obtained definitions will not be equivalent (see Example 6 below).
Definition 11 Let a be an agent,
![]() $B_a$
be its belief base and
$B_a$
be its belief base and
![]() $G_a$
be its set of goals. Let
$G_a$
be its set of goals. Let
![]() $\varphi_1$
and
$\varphi_1$
and
![]() $\varphi_2$
be two formulas of
$\varphi_2$
be two formulas of
![]() $L \setminus L_G$
.
$L \setminus L_G$
.
![]() $\varphi_1$
is at least as useful for a as
$\varphi_1$
is at least as useful for a as
![]() $\varphi_2$
, denoted by
$\varphi_2$
, denoted by
![]() $\varphi_2 \preceq_u^1 \varphi_1$
, if and only if
$\varphi_2 \preceq_u^1 \varphi_1$
, if and only if
![]() $Missing(B_a \cup \varphi_1, G_a) \preceq^1 Missing(B_a \cup \varphi_2, G_a)$
.
$Missing(B_a \cup \varphi_1, G_a) \preceq^1 Missing(B_a \cup \varphi_2, G_a)$
.
![]() $\varphi_1$
is strictly more useful for a than
$\varphi_1$
is strictly more useful for a than
![]() $\varphi_2$
, denoted by
$\varphi_2$
, denoted by
![]() $\varphi_2 \prec_u^1 \varphi_1$
, if and only if
$\varphi_2 \prec_u^1 \varphi_1$
, if and only if
![]() $\varphi_2 \preceq^1 \varphi_1$
and
$\varphi_2 \preceq^1 \varphi_1$
and
![]() $\varphi_1 \not \preceq^1 \varphi_2$
. Finally,
$\varphi_1 \not \preceq^1 \varphi_2$
. Finally,
![]() $\varphi_1$
is as useful for a as
$\varphi_1$
is as useful for a as
![]() $\varphi_2$
, denoted by
$\varphi_2$
, denoted by
![]() $\sim_u^1$
, if and only if
$\sim_u^1$
, if and only if
![]() $\varphi_2 \preceq_u^1 \varphi_1$
and
$\varphi_2 \preceq_u^1 \varphi_1$
and
![]() $\varphi_1 \preceq_u^1 \varphi_2$
.
$\varphi_1 \preceq_u^1 \varphi_2$
.
According to this definition, if one piece of information allows to achieve more goals than another, then it is more useful. If it makes it possible to achieve the same number of goals but if, for at least one goal, it makes it possible to reduce missing information, then it is more useful.
Definition 12 Let a be an agent,
![]() $B_a$
be its belief base and
$B_a$
be its belief base and
![]() $G_a$
be its set of goals. Let
$G_a$
be its set of goals. Let
![]() $\varphi_1$
and
$\varphi_1$
and
![]() $\varphi_2$
be two formulas of
$\varphi_2$
be two formulas of
![]() $L \setminus L_G$
.
$L \setminus L_G$
.
![]() $\varphi_1$
is at least as useful for a as
$\varphi_1$
is at least as useful for a as
![]() $\varphi_2$
, denoted by
$\varphi_2$
, denoted by
![]() $\varphi_2 \preceq_u^2 \varphi_1$
, if and only if
$\varphi_2 \preceq_u^2 \varphi_1$
, if and only if
![]() $Missing(B_a \cup \varphi_1, G_a) \preceq^2 Missing(B_a \cup \varphi_2, G_a)$
.
$Missing(B_a \cup \varphi_1, G_a) \preceq^2 Missing(B_a \cup \varphi_2, G_a)$
.
![]() $\varphi_1$
is strictly more useful for a than
$\varphi_1$
is strictly more useful for a than
![]() $\varphi_2$
, denoted by
$\varphi_2$
, denoted by
![]() $\varphi_2 \prec_u^2 \varphi_1$
, if and only if
$\varphi_2 \prec_u^2 \varphi_1$
, if and only if
![]() $\varphi_2 \preceq_U^2 \varphi_1$
and
$\varphi_2 \preceq_U^2 \varphi_1$
and
![]() $\varphi_1 \not \preceq_U^2 \varphi_2$
. Finally,
$\varphi_1 \not \preceq_U^2 \varphi_2$
. Finally,
![]() $\varphi_1$
is as useful for a as
$\varphi_1$
is as useful for a as
![]() $\varphi_2$
, denoted by
$\varphi_2$
, denoted by
![]() $\sim_u^2$
, if and only if
$\sim_u^2$
, if and only if
![]() $\varphi_2 \preceq_u^2 \varphi_1$
and
$\varphi_2 \preceq_u^2 \varphi_1$
and
![]() $\varphi_1 \preceq_u^2 \varphi_2$
.
$\varphi_1 \preceq_u^2 \varphi_2$
.
According to this definition, if one piece of information allows to achieve more goals than another, then it is more useful. If it achieves the same number of goals and if the missing information is generally shorter, then it is more useful.
These two definitions are not equivalent, as shown below.
Example 6 Let us suppose that:
![]() $G_a = \{g_1,g_2\}$
and
$G_a = \{g_1,g_2\}$
and
![]() $B_a^G = \{p \wedge q \rightarrow g_1, p \wedge r \rightarrow g_2\}$
. We have for instance,
$B_a^G = \{p \wedge q \rightarrow g_1, p \wedge r \rightarrow g_2\}$
. We have for instance,
![]() $Missing(B_a \cup (p \wedge x), G_a) = \{q,r\}$
and
$Missing(B_a \cup (p \wedge x), G_a) = \{q,r\}$
and
![]() $Missing(B_a \cup r, G_a) = \{p \wedge q, p\}$
. Thus,
$Missing(B_a \cup r, G_a) = \{p \wedge q, p\}$
. Thus,
![]() $r \prec_u^2 (p \wedge x)$
but
$r \prec_u^2 (p \wedge x)$
but
![]() $r \not\prec_u^1 (p \wedge x)$
.
$r \not\prec_u^1 (p \wedge x)$
.
Proposition 6 If
![]() $\psi \models \varphi$
then
$\psi \models \varphi$
then
![]() $\varphi\;\preceq_U^1\;\psi$
and
$\varphi\;\preceq_U^1\;\psi$
and
![]() $\varphi\;\preceq_U^2\;\psi$
.
$\varphi\;\preceq_U^2\;\psi$
.
Proof Suppose
![]() $\psi \models \varphi$
. The second item of Proposition 1 allows us to conclude
$\psi \models \varphi$
. The second item of Proposition 1 allows us to conclude
![]() $Missing(B_a \cup \psi,g) \subseteq Missing(B_a \cup \varphi,g)$
for any
$Missing(B_a \cup \psi,g) \subseteq Missing(B_a \cup \varphi,g)$
for any
![]() $g \in G_a$
and thus,
$g \in G_a$
and thus,
![]() $ Missing(B_a \cup \psi,G_a) \subseteq Missing(B_a \cup \varphi,G_a)$
.
$ Missing(B_a \cup \psi,G_a) \subseteq Missing(B_a \cup \varphi,G_a)$
.
First suppose that
![]() $\mid Missing(B_a \cup \psi,G_a) \mid \lt \mid Missing(B_a \cup \varphi,G_a)\mid$
. In this case,
$\mid Missing(B_a \cup \psi,G_a) \mid \lt \mid Missing(B_a \cup \varphi,G_a)\mid$
. In this case,
![]() $Missing(B_a \cup \varphi,G_a) \preceq^1 Missing(B_a \cup \psi,G_a)$
and
$Missing(B_a \cup \varphi,G_a) \preceq^1 Missing(B_a \cup \psi,G_a)$
and
![]() $Missing(B_a \cup \varphi,G_a) \preceq^2 Missing(B_a \cup \psi,G_a)$
. Thus,
$Missing(B_a \cup \varphi,G_a) \preceq^2 Missing(B_a \cup \psi,G_a)$
. Thus,
![]() $\varphi \preceq^1 \psi$
and
$\varphi \preceq^1 \psi$
and
![]() $\varphi\;\preceq_U^2\;\psi$
.
$\varphi\;\preceq_U^2\;\psi$
.
Suppose now that
![]() $\mid Missing(B_a \cup \psi,G_a) \mid = \mid Missing(B_a \cup \varphi,G_a)\mid$
. We consider the bijection which associates, for any goal g in
$\mid Missing(B_a \cup \psi,G_a) \mid = \mid Missing(B_a \cup \varphi,G_a)\mid$
. We consider the bijection which associates, for any goal g in
![]() $G_a$
, the element
$G_a$
, the element
![]() $Missing(B_a \cup \psi,g)$
of
$Missing(B_a \cup \psi,g)$
of
![]() $Missing(B_a \cup \psi,G_a)$
to the element
$Missing(B_a \cup \psi,G_a)$
to the element
![]() $Missing(B_a \cup \varphi,g)$
of
$Missing(B_a \cup \varphi,g)$
of
![]() $Missing(B_a \cup \varphi,G_a)$
. Since
$Missing(B_a \cup \varphi,G_a)$
. Since
![]() $Missing(B_a \cup \psi,g) \subseteq Missing(B_a \cup \varphi,g)$
, we have
$Missing(B_a \cup \psi,g) \subseteq Missing(B_a \cup \varphi,g)$
, we have
![]() $\mid Missing(B_a \cup \psi,g)\mid \leq \mid Missing(B_a \cup \varphi,g)\mid $
. This proves
$\mid Missing(B_a \cup \psi,g)\mid \leq \mid Missing(B_a \cup \varphi,g)\mid $
. This proves
![]() $\varphi \preceq^1 \psi$
and
$\varphi \preceq^1 \psi$
and
![]() $\varphi\;\preceq_U^2\;\psi$
.
$\varphi\;\preceq_U^2\;\psi$
.
In words, the logical consequence of a formula is at least as useful as the formula.
6. A numerical approach
The numerical approach we propose here has its bases in an informal survey we conducted with 30 people of different ages. We have considered different non achieved goals and the lists of pieces of information needed to achieve those goals. Survey participants were asked which information was of most interest to them: (i) information that allows them to get closer to more than one goal, without achieving none of them, (ii) information that allows them to achieve a single goal and does not contribute to any other goal, or (iii) information that allows them to both achieve one goal and to get closer to the other goals. What emerged from the answers is that of course people prefer to achieve one goal and getting closer to other goals, but what is more surprising is that people would rather prefer to have at least one goal achieved than to be closer to achieving several goals! However, if none of the goals can be achieved, most people prefer information that allows them to get closer to most of the goals. Another interesting point is that people are not interested at all in having more information than necessary, which is consistent with Grice’s principle, by the way. The postulates we are proposing here are in line with the results of this survey.
6.1. Postulates for a usefulness measure
In this section, we follow a numerical approach by associating each piece of information with a usefulness degree. To begin with, we state some rationality postulates, which are based on the results of our survey, such a measure must satisfy. The general case will not be treated, and we will limit ourselves to calculating the degree of usefulness of conjunctions of positive literals.
Again, consider an agent a with its belief base
![]() $B_a$
and its goal base
$B_a$
and its goal base
![]() $G_a$
. Let
$G_a$
. Let
![]() $\varphi$
be a conjunction of positive literals. We define:
$\varphi$
be a conjunction of positive literals. We define:
-
 $ E_{B_a}(\varphi) = \{g \in G_a, B_a \not\models g \;and\; B_a \cup \varphi \models g\}$
$ E_{B_a}(\varphi) = \{g \in G_a, B_a \not\models g \;and\; B_a \cup \varphi \models g\}$
-
 $Cons(B_a,\varphi) = \{l\; positive \; literal\;of\;L\;:\; B_a \cup \varphi \models l\}$
$Cons(B_a,\varphi) = \{l\; positive \; literal\;of\;L\;:\; B_a \cup \varphi \models l\}$
-
 $N_m(\varphi)= \Sigma_{g \in G_a} Min_{C \in Missing(B_a,g)} |C \setminus Cons(B_a,\varphi)|$
$N_m(\varphi)= \Sigma_{g \in G_a} Min_{C \in Missing(B_a,g)} |C \setminus Cons(B_a,\varphi)|$
-
 $N_u(\varphi) = |\varphi \setminus \cup_{g \in G_a} \cup_{C \in Missing(B_a,g)} C|$
$N_u(\varphi) = |\varphi \setminus \cup_{g \in G_a} \cup_{C \in Missing(B_a,g)} C|$
![]() $ E_{B_a}(\varphi)$
is the set of goals that a can achieve after adding
$ E_{B_a}(\varphi)$
is the set of goals that a can achieve after adding
![]() $\varphi$
to its beliefs. Thus,
$\varphi$
to its beliefs. Thus,
![]() $\mid E_{B_a}(\varphi) \mid $
is the number of goals that a can achieve after adding
$\mid E_{B_a}(\varphi) \mid $
is the number of goals that a can achieve after adding
![]() $\varphi$
to its beliefs.
$\varphi$
to its beliefs.
![]() $Cons(B_a,\varphi)$
is the set of positive literals of L that are deducible from
$Cons(B_a,\varphi)$
is the set of positive literals of L that are deducible from
![]() $B_a \cup \varphi$
.
$B_a \cup \varphi$
.
![]() $N_m(\varphi)$
sums, for all goals in
$N_m(\varphi)$
sums, for all goals in
![]() $G_a$
, the smallest number of literals that are missing to achieve the goals and that are not deductible from
$G_a$
, the smallest number of literals that are missing to achieve the goals and that are not deductible from
![]() $B_a \cup \varphi$
. The smaller
$B_a \cup \varphi$
. The smaller
![]() $N_m(\varphi)$
, the more
$N_m(\varphi)$
, the more
![]() $\varphi$
reduces information which are missing to achieve the goals.
$\varphi$
reduces information which are missing to achieve the goals.
![]() $N_u(\varphi)$
counts the positive literals deducible from
$N_u(\varphi)$
counts the positive literals deducible from
![]() $B_a \cup \varphi$
that are not literals of missing information. Adding them is therefore not useful to achieve the goals. Thus, the greater
$B_a \cup \varphi$
that are not literals of missing information. Adding them is therefore not useful to achieve the goals. Thus, the greater
![]() $N_u(\varphi)$
, the more
$N_u(\varphi)$
, the more
![]() $\varphi$
brings non useful information.
$\varphi$
brings non useful information.
Example 7
![]() $B_a^W = \emptyset$
,
$B_a^W = \emptyset$
,
![]() $B_a^G = \{p \rightarrow g_1, q \rightarrow g_1, r \wedge s \rightarrow g_2\}$
.
$B_a^G = \{p \rightarrow g_1, q \rightarrow g_1, r \wedge s \rightarrow g_2\}$
.
![]() $Missing(B_a,g_1) = \{p \vee q\}$
,
$Missing(B_a,g_1) = \{p \vee q\}$
,
![]() $Missing(B_a,g_2) = \{r \wedge s\}$
. Table 1 illustrates these different numbers for different formulas.
$Missing(B_a,g_2) = \{r \wedge s\}$
. Table 1 illustrates these different numbers for different formulas.
Let
![]() $U(\varphi)$
be a real number representing how much
$U(\varphi)$
be a real number representing how much
![]() $\varphi$
is useful for a. We have based our definition on the following postulates.
$\varphi$
is useful for a. We have based our definition on the following postulates.
Monotonicity on the number of goals
(P1)
![]() $|E(\varphi_1)| \lt |E(\varphi_2)| \;\Longrightarrow\; $
$|E(\varphi_1)| \lt |E(\varphi_2)| \;\Longrightarrow\; $
![]() $ U(\varphi_1) \lt U(\varphi_2)$
.
$ U(\varphi_1) \lt U(\varphi_2)$
.
Table 1. The values of
![]() $N_m$
and
$N_m$
and
![]() $N_u$
measurements
$N_u$
measurements

The number of goals that a piece of information allows an agent to achieve should influence the degree of usefulness of such a piece of information for the agent. Intuitively, a piece of information which allows to achieve a higher number of goals (with respect to another piece of information) should be more useful.
Monotonicity on the quantity of information needed:
(P2)
![]() $|E(\varphi_1)| = |E(\varphi_2)|$
and
$|E(\varphi_1)| = |E(\varphi_2)|$
and
![]() $N_m(\varphi_1) \lt N_m(\varphi_2) \Longrightarrow U(\varphi_1) \gt U(\varphi_2)$
.
$N_m(\varphi_1) \lt N_m(\varphi_2) \Longrightarrow U(\varphi_1) \gt U(\varphi_2)$
.
The amount of missing information (needed information) provided by a formula should influence its degree of usefulness. Intuitively, when two formulas allow to achieve the same number of goals, one of them is more useful than the other if it further reduces the number of missing information.
Monotonicity on the quantity of useless information:
(P3)
![]() $|E(\varphi_1)| = |E(\varphi_2)|$
and
$|E(\varphi_1)| = |E(\varphi_2)|$
and
![]() $N_m(\varphi_1)=N_m(\varphi_2)$
and
$N_m(\varphi_1)=N_m(\varphi_2)$
and
![]() $N_u(\varphi_1)\lt N_u(\varphi_2) \Longrightarrow U(\varphi_1) \gt U(\varphi_2)$
.
$N_u(\varphi_1)\lt N_u(\varphi_2) \Longrightarrow U(\varphi_1) \gt U(\varphi_2)$
.
The amount of useless information conveyed by a piece of information should also influence its degree of usefulness. Intuitively, when two formulas allow to achieve the same number of goals, a formula is more useful than another if it provides less useless information than the other. This idea agrees with the maximin principle of Grice’s. Useless information while not being harmful in view of reaching a goal may produce an additional overhead on whom has to process it which may be qualified as a cost.
Equality:
P4
![]() $|E(\varphi_1)| = |E(\varphi_2)|$
and
$|E(\varphi_1)| = |E(\varphi_2)|$
and
![]() $N_m(\varphi_1) = N_m(\varphi_2)$
and
$N_m(\varphi_1) = N_m(\varphi_2)$
and
![]() $N_u(\varphi_1) = N_u(\varphi_2) \Longrightarrow U(\varphi_1) = U(\varphi_2)$
.
$N_u(\varphi_1) = N_u(\varphi_2) \Longrightarrow U(\varphi_1) = U(\varphi_2)$
.
Two pieces of information which allow to achieve the same number of goals, and which have exactly the same amount of useful and useless information should have the same degree of usefulness.
6.2. The usefulness measure U
In this section we will present an extension of the numerical measure of usefulness proposed in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019):
Definition 13 Let a be an agent whose goals are in
![]() $G_a$
and let
$G_a$
and let
![]() $\varphi$
be a conjunction of positive literals. The usefulness degreeFootnote 2 has been defined as follows:
$\varphi$
be a conjunction of positive literals. The usefulness degreeFootnote 2 has been defined as follows:
 \begin{align*} U(\varphi) = \frac{1}{|G_a| + 1}\left[|E(\varphi)| + \frac{N_1(\varphi)}{N_1(\varphi) + N_2(\varphi) + \frac{N_3(\varphi)}{N_3(\varphi) + 1}}\right]\end{align*}
\begin{align*} U(\varphi) = \frac{1}{|G_a| + 1}\left[|E(\varphi)| + \frac{N_1(\varphi)}{N_1(\varphi) + N_2(\varphi) + \frac{N_3(\varphi)}{N_3(\varphi) + 1}}\right]\end{align*}
![]() $N_1(\varphi)$
quantifies the useful part of
$N_1(\varphi)$
quantifies the useful part of
![]() $\varphi$
for the agent, while
$\varphi$
for the agent, while
![]() $N_2(\varphi)$
quantifies the agent’s disappointment (lack of needed information) toward
$N_2(\varphi)$
quantifies the agent’s disappointment (lack of needed information) toward
![]() $\varphi$
and, finally,
$\varphi$
and, finally,
![]() $N_3(\varphi)$
quantifies the disturbance caused to the agent by the unexpected and unnecessary content of
$N_3(\varphi)$
quantifies the disturbance caused to the agent by the unexpected and unnecessary content of
![]() $\varphi$
. The above definition of usefulness takes these three aspects into consideration.
$\varphi$
. The above definition of usefulness takes these three aspects into consideration.
The intuitive idea behind this definition of usefulness is as follows. The usefulness of information can be seen as a calculation of the similarity between the information the agent needs to achieve its goals and the piece of information that arrives. The more direct or indirect elements (that can be deduced) there are in common between the two, the more useful the information will be. We would like to stress that this fact allows to account for the serendipity factor (Toms, Reference Toms2000) in the definition of usefulness. Indeed, an agent gets (asks for) a piece of information to achieve a given goal, but if the received piece of information also enables other goals to be achieved, this fact is taken into considered in the computation of the usefulness. However, the number of common elements is not always enough to distinguish the degrees of usefulness between two pieces of information. Indeed, in some cases it would also be necessary to take into account their differences. We have been inspired by Tversky’s idea (Tversky, 1977), according to which, in order to calculate the similarity between two objects A and B, we should consider, in addition to what they have in common, what distinguishes them, that is, the features of A which are not features of B and vice versa. This is the reason why these three values,
![]() $N_1(\varphi)$
,
$N_1(\varphi)$
,
![]() $N_2(\varphi)$
, and
$N_2(\varphi)$
, and
![]() $N_3(\varphi)$
, we have been considered.
$N_3(\varphi)$
, we have been considered.
Here,
![]() $N_1(\varphi)$
is no longer needed; for the sake of intuitiveness, the extension of
$N_1(\varphi)$
is no longer needed; for the sake of intuitiveness, the extension of
![]() $N_2(\varphi)$
will be renamed
$N_2(\varphi)$
will be renamed
![]() $N_m(\varphi)$
(for ‘number of missing [literals]’) and the extension of
$N_m(\varphi)$
(for ‘number of missing [literals]’) and the extension of
![]() $N_3(\varphi)$
will be renamed
$N_3(\varphi)$
will be renamed
![]() $N_u(\varphi)$
(for ‘number of useless or unexpected [literals]’).
$N_u(\varphi)$
(for ‘number of useless or unexpected [literals]’).
Table 2. The values of
![]() $N_m$
,
$N_m$
,
![]() $N_u$
, and U measurements
$N_u$
, and U measurements

This gives the following extension of Definition 13.
Definition 14 We denote
![]() $\alpha_a = \Sigma_{g \in G_a} Min_{C \in Missing(B_a,g)} \mid C \mid$
. Then the usefulness measure U is defined by:
$\alpha_a = \Sigma_{g \in G_a} Min_{C \in Missing(B_a,g)} \mid C \mid$
. Then the usefulness measure U is defined by:
 \begin{align*} U(\varphi) = \frac{1}{|G_a| + 1}\left[|E(\varphi)| + \frac{\alpha_a - N_m(\varphi)}{\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}}\right].\end{align*}
\begin{align*} U(\varphi) = \frac{1}{|G_a| + 1}\left[|E(\varphi)| + \frac{\alpha_a - N_m(\varphi)}{\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}}\right].\end{align*}
![]() $N_m(\varphi)$
quantifies how far the agent is from achieving its goals after acquiring
$N_m(\varphi)$
quantifies how far the agent is from achieving its goals after acquiring
![]() $\varphi$
, while
$\varphi$
, while
![]() $N_u(\varphi)$
quantifies the disturbance caused to the agent by the unexpected and unnecessary content of
$N_u(\varphi)$
quantifies the disturbance caused to the agent by the unexpected and unnecessary content of
![]() $\varphi$
.
$\varphi$
.
Example 8 Let us now consider the following example, which illustrates how our definition of usefulness takes into account both the novelty (relative to what the agent already believes) and the serendipity of a piece of information.
![]() $B_a^W = \{r\}$
(the agent already believes r),
$B_a^W = \{r\}$
(the agent already believes r),
![]() $B_a^G = \{p \rightarrow g_1, q \rightarrow g_1, p \wedge r \wedge s \rightarrow g_2\}$
.
$B_a^G = \{p \rightarrow g_1, q \rightarrow g_1, p \wedge r \wedge s \rightarrow g_2\}$
.
![]() $Missing(B_a,g_1) = \{p \vee q\}$
,
$Missing(B_a,g_1) = \{p \vee q\}$
,
![]() $Missing(B_a,g_2) = \{p \wedge s\}$
. Table 2 illustrates these different numbers for different formulas. We have
$Missing(B_a,g_2) = \{p \wedge s\}$
. Table 2 illustrates these different numbers for different formulas. We have
![]() $ \alpha_a = 3$
.
$ \alpha_a = 3$
.
In words,
![]() $p \wedge s$
is the piece of information that has the maximal degree of usefulness, 1. This is explained by the fact that adding
$p \wedge s$
is the piece of information that has the maximal degree of usefulness, 1. This is explained by the fact that adding
![]() $p \wedge s$
allows to achieve both goals
$p \wedge s$
allows to achieve both goals
![]() $g_1$
and
$g_1$
and
![]() $g_2$
without adding useless information as it is instead the case for
$g_2$
without adding useless information as it is instead the case for
![]() $p \wedge s \wedge x $
, which, indeed, has a slightly lower degree of usefulness,
$p \wedge s \wedge x $
, which, indeed, has a slightly lower degree of usefulness,
![]() $\frac{11}{12}$
. The usefulness of p,
$\frac{11}{12}$
. The usefulness of p,
![]() $\frac{5}{9}$
, is higher than the usefulness of q,
$\frac{5}{9}$
, is higher than the usefulness of q,
![]() $\frac{4}{9}$
, because while both allow to achieve goal
$\frac{4}{9}$
, because while both allow to achieve goal
![]() $g_1$
, p, unlike q, allows in addition, to reduce the ‘distance’ from achieving
$g_1$
, p, unlike q, allows in addition, to reduce the ‘distance’ from achieving
![]() $g_2$
(serendipity); the usefulness of p is also higher than the usefulness of
$g_2$
(serendipity); the usefulness of p is also higher than the usefulness of
![]() $p \wedge x$
,
$p \wedge x$
,
![]() $ \frac{1}{2}$
, because x is not useful for achieving any goal. However,
$ \frac{1}{2}$
, because x is not useful for achieving any goal. However,
![]() $p \wedge x$
is as useful as
$p \wedge x$
is as useful as
![]() $p \wedge r$
, although for a different reason: r is not novel for the agent. Finally, the usefulness of
$p \wedge r$
, although for a different reason: r is not novel for the agent. Finally, the usefulness of
![]() $p \wedge q$
is the same as the usefulness of p because having q in addition to p does not decrease the distance from achieving any further goal.
$p \wedge q$
is the same as the usefulness of p because having q in addition to p does not decrease the distance from achieving any further goal.
Proposition 7 We can notice that for any conjunction of positive literals
![]() $\varphi$
we have:
$\varphi$
we have:
Proof
-
First we notice that
 $N_m(\varphi) \leq \alpha_a$
. Indeed
$N_m(\varphi) \leq \alpha_a$
. Indeed
 $\forall g \in G_a\; \forall C \in Missing(B_a,g)\;\mid C \setminus Cons(\varphi) \mid \leq \mid C \mid$
. Thus,
$\forall g \in G_a\; \forall C \in Missing(B_a,g)\;\mid C \setminus Cons(\varphi) \mid \leq \mid C \mid$
. Thus,
 $\forall g \in G_a\; Min_{C \in Missing(B_a,g)} \mid C \setminus Cons(\varphi) \mid \leq Min_{C \in G_a} \mid C \mid$
. Finally,
$\forall g \in G_a\; Min_{C \in Missing(B_a,g)} \mid C \setminus Cons(\varphi) \mid \leq Min_{C \in G_a} \mid C \mid$
. Finally,
 $\Sigma_{g \in G_a} Min_{C \in Missing(B_a,g)} \leq \Sigma_{g \in G_a} \mid C \mid$
Thus,
$\Sigma_{g \in G_a} Min_{C \in Missing(B_a,g)} \leq \Sigma_{g \in G_a} \mid C \mid$
Thus,
 $\alpha_a - N_m(\varphi)$
is positive.
$\alpha_a - N_m(\varphi)$
is positive.Moreover,
 $\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}$
is positive. Thus,
$\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}$
is positive. Thus,
 $\frac{\alpha_a - N_m(\varphi)}{\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}}$
is positive.
$\frac{\alpha_a - N_m(\varphi)}{\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}}$
is positive.Besides
 $\alpha_a - N_m(\varphi) \leq \alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}$
. Thus,
$\alpha_a - N_m(\varphi) \leq \alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}$
. Thus,
 $\frac{\alpha_a - N_m(\varphi)}{\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}} \leq 1$
$\frac{\alpha_a - N_m(\varphi)}{\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}} \leq 1$
-
 $\frac{\alpha_a - N_m(\varphi)}{\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}} = 1$
implies
$\frac{\alpha_a - N_m(\varphi)}{\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}} = 1$
implies
 $\alpha_a - N_m(\varphi) = \alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}$
. Thus,
$\alpha_a - N_m(\varphi) = \alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}$
. Thus,
 $\frac{N_u(\varphi)}{N_u(\varphi) + 1} + N_m(\varphi) = 0$
. Since these two numbers are positive, this implies
$\frac{N_u(\varphi)}{N_u(\varphi) + 1} + N_m(\varphi) = 0$
. Since these two numbers are positive, this implies
 $N_m(\varphi) = N3(\varphi) = 0$
. Finally,
$N_m(\varphi) = N3(\varphi) = 0$
. Finally,
 $N_m(\varphi)=0$
implies that any goal is achieved that is
$N_m(\varphi)=0$
implies that any goal is achieved that is
 $E(\varphi) = G_a$
.
$E(\varphi) = G_a$
.
Proposition 8 The measure
![]() $U(\varphi)$
proposed in Definition 14 satisfies postulates (P1)–(P4).
$U(\varphi)$
proposed in Definition 14 satisfies postulates (P1)–(P4).
-
(P1). Suppose
 $|E(\varphi_1)| \lt |E(\varphi_2)| $
. Then
$|E(\varphi_1)| \lt |E(\varphi_2)| $
. Then
 $|E(\varphi_1)| + 1 \leq |E(\varphi_2)|.$
Suppose now
$|E(\varphi_1)| + 1 \leq |E(\varphi_2)|.$
Suppose now
 $ \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}} = 1. $
This would imply (by Proposition 7)
$ \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}} = 1. $
This would imply (by Proposition 7)
 $|E(\varphi_1)| = |G_a|$
. This is impossible because
$|E(\varphi_1)| = |G_a|$
. This is impossible because
 $|E(\varphi_1)| \lt |E(\varphi_2)| $
. Thus,
$|E(\varphi_1)| \lt |E(\varphi_2)| $
. Thus,
 $ \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}} \lt 1. $
Thus,
$ \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}} \lt 1. $
Thus,
 $|E(\varphi_1)| + \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}} \lt |E(\varphi_2)|$
. Finally,
$|E(\varphi_1)| + \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}} \lt |E(\varphi_2)|$
. Finally,
 $U(\varphi_1) \lt U(\varphi_2)$
.
$U(\varphi_1) \lt U(\varphi_2)$
. -
(P2) Suppose
 $|E(\varphi_1)| = |E(\varphi_2)|$
and
$|E(\varphi_1)| = |E(\varphi_2)|$
and
 $N_m(\varphi_1) \lt N_m(\varphi_2)$
$N_m(\varphi_1) \lt N_m(\varphi_2)$
We denote
 $U = \frac{N_u(\varphi_2)}{N_u(\varphi_2) + 1}$
and
$U = \frac{N_u(\varphi_2)}{N_u(\varphi_2) + 1}$
and
 $V = \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}$
.
$V = \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}$
.Thus,
 $ U(\varphi_2) - U(\varphi_1) = \frac{1}{|G_a| + 1}\left[\frac{\alpha_a - N_m(\varphi_2)}{\alpha_a + U} - \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + V}\right] $
$ U(\varphi_2) - U(\varphi_1) = \frac{1}{|G_a| + 1}\left[\frac{\alpha_a - N_m(\varphi_2)}{\alpha_a + U} - \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + V}\right] $
We distinguish 3 cases:
-
–
 $U = V$
. We denote
$U = V$
. We denote
 $\alpha_a + U = \alpha_a + V = D'$
. Then
$\alpha_a + U = \alpha_a + V = D'$
. Then $ U(\varphi_2) - U(\varphi_1) = \frac{- N_m(\varphi_2) + N_m(\varphi_1)}{D'} \lt 0$
, because
$ U(\varphi_2) - U(\varphi_1) = \frac{- N_m(\varphi_2) + N_m(\varphi_1)}{D'} \lt 0$
, because
 $N_m(\varphi_1) \lt N_m(\varphi_2)$
.
$N_m(\varphi_1) \lt N_m(\varphi_2)$
. -
–
 $U \lt V \Rightarrow \frac{1}{\alpha_a + V} \lt \frac{1}{\alpha_a + U} \Rightarrow \frac{- N_m(\varphi_2)}{\alpha_a + U} \lt \frac{- N_m(\varphi_1)}{\alpha_a + V} \\[5pt] \Rightarrow \frac{\alpha_a - N_m(\varphi_2)}{\alpha_a + U} \lt \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + V} \Rightarrow U(\varphi_2) - U(\varphi_1) \lt 0$
$U \lt V \Rightarrow \frac{1}{\alpha_a + V} \lt \frac{1}{\alpha_a + U} \Rightarrow \frac{- N_m(\varphi_2)}{\alpha_a + U} \lt \frac{- N_m(\varphi_1)}{\alpha_a + V} \\[5pt] \Rightarrow \frac{\alpha_a - N_m(\varphi_2)}{\alpha_a + U} \lt \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + V} \Rightarrow U(\varphi_2) - U(\varphi_1) \lt 0$
-
–
 $V \lt U \Rightarrow \frac{1}{\alpha_a + U} \lt \frac{1}{\alpha_a + V} \Rightarrow \frac{N_m(\varphi_1)}{\alpha_a + U} \lt \frac{N_m(\varphi_2)}{\alpha_a + V} \Rightarrow \frac{- N_m(\varphi_2)}{\alpha_a + V} \lt \frac{- N_m(\varphi_1)}{\alpha_a + U}\\[5pt] \Rightarrow \frac{\alpha_a - N_m(\varphi_2)}{\alpha_a + V} \lt \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + U} \\[5pt] \Rightarrow \frac{\alpha_a - N_m(\varphi_2)}{\alpha_a + U} \lt \frac{\alpha_a - N_m(\varphi_2)}{\alpha_a + V} \lt \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + U} \lt \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + V} \\[5pt] \Rightarrow U(\varphi_2) - U(\varphi_1) \lt 0$
$V \lt U \Rightarrow \frac{1}{\alpha_a + U} \lt \frac{1}{\alpha_a + V} \Rightarrow \frac{N_m(\varphi_1)}{\alpha_a + U} \lt \frac{N_m(\varphi_2)}{\alpha_a + V} \Rightarrow \frac{- N_m(\varphi_2)}{\alpha_a + V} \lt \frac{- N_m(\varphi_1)}{\alpha_a + U}\\[5pt] \Rightarrow \frac{\alpha_a - N_m(\varphi_2)}{\alpha_a + V} \lt \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + U} \\[5pt] \Rightarrow \frac{\alpha_a - N_m(\varphi_2)}{\alpha_a + U} \lt \frac{\alpha_a - N_m(\varphi_2)}{\alpha_a + V} \lt \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + U} \lt \frac{\alpha_a - N_m(\varphi_1)}{\alpha_a + V} \\[5pt] \Rightarrow U(\varphi_2) - U(\varphi_1) \lt 0$
-
(P3) Suppose
 $|E(\varphi_1)| = |E(\varphi_2)|$
,
$|E(\varphi_1)| = |E(\varphi_2)|$
,
 $N_m(\varphi_1)=N_m(\varphi_2)$
and
$N_m(\varphi_1)=N_m(\varphi_2)$
and
 $N_u(\varphi_1)\lt N_u(\varphi_2)$
. Since
$N_u(\varphi_1)\lt N_u(\varphi_2)$
. Since
 $N_u(\varphi_1)\lt N_u(\varphi_2)$
we also have
$N_u(\varphi_1)\lt N_u(\varphi_2)$
we also have
 $ \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1} \lt \frac{N_u(\varphi_2)}{N_u(\varphi_2) + 1}$
. Thus,
$ \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1} \lt \frac{N_u(\varphi_2)}{N_u(\varphi_2) + 1}$
. Thus,
 $\frac{1}{\alpha_a + \frac{N_u(\varphi_2)}{N_u(\varphi_2) + 1}} \lt \frac{1}{\alpha_a + \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}}$
.
$\frac{1}{\alpha_a + \frac{N_u(\varphi_2)}{N_u(\varphi_2) + 1}} \lt \frac{1}{\alpha_a + \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}}$
.We denote
 $\alpha_a - N_m(\varphi_1) = \alpha_a - N_m(\varphi_2) = k$
.
$\alpha_a - N_m(\varphi_1) = \alpha_a - N_m(\varphi_2) = k$
.Then
 $\frac{k}{\alpha_a + \frac{N_u(\varphi_2)}{N_u(\varphi_2) + 1}} \lt \frac{k}{\alpha_a + \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}}$
. Finally,
$\frac{k}{\alpha_a + \frac{N_u(\varphi_2)}{N_u(\varphi_2) + 1}} \lt \frac{k}{\alpha_a + \frac{N_u(\varphi_1)}{N_u(\varphi_1) + 1}}$
. Finally,
 $U(\varphi_2) \lt U(\varphi_1)$
$U(\varphi_2) \lt U(\varphi_1)$
-
(P4) Straightforward.
6.3. Particular case
In this section, we consider the particular case in which there is only one way to achieve each goal that is,
![]() $\forall g \in G_a$
$\forall g \in G_a$
![]() $n_g = 1$
, which was the case considered in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019).
$n_g = 1$
, which was the case considered in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019).
-
First, we prove that the definition of U given in Definition 14 is an extension of the definition of U given in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019). Indeed, under this assumption, we have:
-
–
 $N_m(\varphi)= \Sigma_{g \in G_a} |Missing(B_a,g) \setminus Cons(B_a,\varphi)|$
$N_m(\varphi)= \Sigma_{g \in G_a} |Missing(B_a,g) \setminus Cons(B_a,\varphi)|$
-
–
 $N_u(\varphi) = |\varphi \setminus \cup_{g \in G_a} Missing(B_a,g) |$
$N_u(\varphi) = |\varphi \setminus \cup_{g \in G_a} Missing(B_a,g) |$
-
–
 $\alpha_a = \Sigma_{g \in G_a} \mid Missing(B_a,g)\mid$
$\alpha_a = \Sigma_{g \in G_a} \mid Missing(B_a,g)\mid$
Now consider the two terms
 $\alpha_a - N_m(\varphi)$
and
$\alpha_a - N_m(\varphi)$
and
 $\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}$
in Definition 14.
$\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1}$
in Definition 14. -
-
–
 $\alpha_a - N_m(\varphi) = \Sigma_{g \in G_a} \mid Missing(B_a,g)\mid -\Sigma_{g \in G_a} |Missing(B_a,g) \setminus Cons(B_a,\varphi)|$
.Thus,
$\alpha_a - N_m(\varphi) = \Sigma_{g \in G_a} \mid Missing(B_a,g)\mid -\Sigma_{g \in G_a} |Missing(B_a,g) \setminus Cons(B_a,\varphi)|$
.Thus,
 $\alpha_a - N_m(\varphi) = \Sigma_{g \in G_a} \mid Missing(B_a,g) \cap Cons(B_a,\varphi) \mid$
.
$\alpha_a - N_m(\varphi) = \Sigma_{g \in G_a} \mid Missing(B_a,g) \cap Cons(B_a,\varphi) \mid$
. -
–
 $\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1} = \Sigma_{g \in G_a} \mid Missing(B_a,g)\mid + \frac{|\varphi \setminus \cup_{g \in G_a} Missing(B_a,g) |}{|\varphi \setminus \cup_{g \in G_a} Missing(B_a,g) | +1}$
$\alpha_a + \frac{N_u(\varphi)}{N_u(\varphi) + 1} = \Sigma_{g \in G_a} \mid Missing(B_a,g)\mid + \frac{|\varphi \setminus \cup_{g \in G_a} Missing(B_a,g) |}{|\varphi \setminus \cup_{g \in G_a} Missing(B_a,g) | +1}$
Thus, U as defined in Definition 14 becomes
This is exactly the one which was given in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019). \begin{align*} U(\varphi) = \frac{1}{|G_a| + 1}\left[|E(\varphi)| +\frac{ \Sigma_{g \in G_a} \mid Missing(B_a,g) \cap Cons(B_a,\varphi) \mid }{\Sigma_{g \in G_a} \mid Missing(B_a,g)\mid +\frac{|\varphi \setminus \cup_{g \in G_a} Missing(B_a,g) |}{|\varphi \setminus \cup_{g \in G_a} Missing(B_a,g) | +1}}\right]\end{align*}
\begin{align*} U(\varphi) = \frac{1}{|G_a| + 1}\left[|E(\varphi)| +\frac{ \Sigma_{g \in G_a} \mid Missing(B_a,g) \cap Cons(B_a,\varphi) \mid }{\Sigma_{g \in G_a} \mid Missing(B_a,g)\mid +\frac{|\varphi \setminus \cup_{g \in G_a} Missing(B_a,g) |}{|\varphi \setminus \cup_{g \in G_a} Missing(B_a,g) | +1}}\right]\end{align*}
-
Moreover, now assume that
 $B_a^W = \emptyset$
. In this case, the only beliefs of the agent concern the agent’s needs in terms of information about the ways to achieve its goals and we have:
$B_a^W = \emptyset$
. In this case, the only beliefs of the agent concern the agent’s needs in terms of information about the ways to achieve its goals and we have:
 $Missing(B_a,g) = premise(g)$
and
$Missing(B_a,g) = premise(g)$
and
 $Cons(B_a,\varphi) = \varphi$
.
$Cons(B_a,\varphi) = \varphi$
.
 $U(\varphi)$
can then be written as: with
$U(\varphi)$
can then be written as: with \begin{align*} U(\varphi) = \frac{1}{| G_a + 1|} \cdot \left[|E(\varphi)| + \frac{ \Sigma_{g \in G_a} |\varphi \cap Premise(g)|}{\Sigma_{g \in G_a} |premise(g)| +\frac{|\varphi \setminus \cup_{g \in G_a} Premise(g)| }{ |\varphi \setminus \cup_{g \in G_a} Premise(g)| + 1}}\right]\end{align*}
\begin{align*} U(\varphi) = \frac{1}{| G_a + 1|} \cdot \left[|E(\varphi)| + \frac{ \Sigma_{g \in G_a} |\varphi \cap Premise(g)|}{\Sigma_{g \in G_a} |premise(g)| +\frac{|\varphi \setminus \cup_{g \in G_a} Premise(g)| }{ |\varphi \setminus \cup_{g \in G_a} Premise(g)| + 1}}\right]\end{align*}
 $E(\varphi) = \{g \in G_a, premise(g) \subseteq \varphi\}$
,
$E(\varphi) = \{g \in G_a, premise(g) \subseteq \varphi\}$
,
-
Now assume that
 $B_a^m = \emptyset$
and
$B_a^m = \emptyset$
and
 $G_a$
is a singleton. In this case, the agent has a single goal,
$G_a$
is a singleton. In this case, the agent has a single goal,
 $g_0$
, and its only beliefs is the formula which expresses the information need for achieving that single goal.
$g_0$
, and its only beliefs is the formula which expresses the information need for achieving that single goal.
 $U(\varphi)$
can then be written as follows: with
$U(\varphi)$
can then be written as follows: with \begin{align*} U(\varphi) = \frac{1}{2} \cdot \left(n(\varphi) + \frac{ |\varphi \cap premise(g_0)| }{ |premise(g_0)| + \frac{|\varphi \setminus premise(g_0)|}{|\varphi \setminus premise(g_0)| + 1}}\right)\end{align*}
\begin{align*} U(\varphi) = \frac{1}{2} \cdot \left(n(\varphi) + \frac{ |\varphi \cap premise(g_0)| }{ |premise(g_0)| + \frac{|\varphi \setminus premise(g_0)|}{|\varphi \setminus premise(g_0)| + 1}}\right)\end{align*}
 $n(\varphi) = 1$
if
$n(\varphi) = 1$
if
 $premise(g_0) \subseteq \varphi$
and
$premise(g_0) \subseteq \varphi$
and
 $n(\varphi) = 0$
otherwise.
$n(\varphi) = 0$
otherwise.
Example 9 Take
![]() $premise(g_0) = a \wedge b$
. Then we have
$premise(g_0) = a \wedge b$
. Then we have
![]() $U(c) = 0$
,
$U(c) = 0$
,
![]() $U(a \wedge c) = 1/5$
,
$U(a \wedge c) = 1/5$
,
![]() $U(a) = 1/4$
,
$U(a) = 1/4$
,
![]() $U(a \wedge b \wedge c) = 9/10$
,
$U(a \wedge b \wedge c) = 9/10$
,
![]() $U(a \wedge b) = 1$
. In other words, c is not useful at all because knowing c does not allow the agent to reach or get closer to its goal.
$U(a \wedge b) = 1$
. In other words, c is not useful at all because knowing c does not allow the agent to reach or get closer to its goal.
![]() $a \wedge c$
is a little more useful, because even if knowing c is not useful to the agent, knowing a allows it to get a little closer to its goal. a is more useful than
$a \wedge c$
is a little more useful, because even if knowing c is not useful to the agent, knowing a allows it to get a little closer to its goal. a is more useful than
![]() $a \wedge c$
because it does not add unnecessary information.
$a \wedge c$
because it does not add unnecessary information.
![]() $a \wedge b \wedge c$
is even more useful because even if it adds unnecessary information, it allows the agent to achieve its goal. Finally,
$a \wedge b \wedge c$
is even more useful because even if it adds unnecessary information, it allows the agent to achieve its goal. Finally,
![]() $a \wedge b$
is the most useful because it allows the agent to reach its goal and does not add any unnecessary information.
$a \wedge b$
is the most useful because it allows the agent to reach its goal and does not add any unnecessary information.
7. An example of application to IR
In this section, we will first recall some relevance dimensions in IR which have been used in the literature (da Costa Pereira et al., Reference da Costa Pereira, Dragoni, Pasi, Boughanem, Berrut, Mothe and Soulé-Dupuy2009) to propose documents to a user (who now takes the place of what we called ‘agent’ in the above general framework). We will then compare those dimensions with the usefulness measure we are proposing here. However, to have a fair comparison, we need to reformulate those dimensions in a logical setting (Abdulahhad et al., Reference Abdulahhad, Berrut, Chevallet and Pasi2019; Lalmas, Reference Lalmas1998; Chen, Reference Chen1994).
7.1. A refresher on relevance dimensions
The aboutness (Cooper, Reference Cooper1971) dimension is a core notion in IR. It is used to compute the topical matching between a document and a user query. However, its modeling gave raise to several distinct interpretations, which characterize a variety of IR models, of which the vector space model is an example. Formally, in the vector space model, a piece of information or, more generally, a document d, can be represented as a vector of T elements,
![]() $d = [w_{1d}, \ldots, w_{T d}]$
. The user interests are represented by a vector
$d = [w_{1d}, \ldots, w_{T d}]$
. The user interests are represented by a vector
![]() $q = [w_{1q}, \ldots, w_{T q}]$
, T being the size of the term vocabulary used. Different choices have been made in the literature regarding the values of
$q = [w_{1q}, \ldots, w_{T q}]$
, T being the size of the term vocabulary used. Different choices have been made in the literature regarding the values of
![]() $w_{id}$
, for example: simply based on the presence or absence of a word in the document, in this case the vector contains values in
$w_{id}$
, for example: simply based on the presence or absence of a word in the document, in this case the vector contains values in
![]() $\{0,1\}$
, or based on the frequency of the word in the document and in the whole repository (TF-IDF) (Baeza-Yates & Ribeiro-Neto, Reference Baeza-Yates and Ribeiro-Neto2011). Here, we will use the vector space model interpretation, and, like in da Costa Pereira et al. (Reference da Costa Pereira, Dragoni, Pasi, Boughanem, Berrut, Mothe and Soulé-Dupuy2009), in addition to the aboutness measure, we will consider the appropriateness dimension (proposed in da Costa Pereira et al., Reference da Costa Pereira, Dragoni, Pasi, Boughanem, Berrut, Mothe and Soulé-Dupuy2009) and the coverage dimension (proposed in Pasi et al., Reference Pasi, Bordogna and Villa2007). We have considered those three relevance dimensions because they explicitly account for the user query/goals. This is not the case for the popularity relevance dimension for example.
$\{0,1\}$
, or based on the frequency of the word in the document and in the whole repository (TF-IDF) (Baeza-Yates & Ribeiro-Neto, Reference Baeza-Yates and Ribeiro-Neto2011). Here, we will use the vector space model interpretation, and, like in da Costa Pereira et al. (Reference da Costa Pereira, Dragoni, Pasi, Boughanem, Berrut, Mothe and Soulé-Dupuy2009), in addition to the aboutness measure, we will consider the appropriateness dimension (proposed in da Costa Pereira et al., Reference da Costa Pereira, Dragoni, Pasi, Boughanem, Berrut, Mothe and Soulé-Dupuy2009) and the coverage dimension (proposed in Pasi et al., Reference Pasi, Bordogna and Villa2007). We have considered those three relevance dimensions because they explicitly account for the user query/goals. This is not the case for the popularity relevance dimension for example.
7.1.1. Aboutness
The term aboutness (topical relevance) is formally defined as follows. Let
![]() $d = [w_{1d} \ldots w_{T d}]$
and
$d = [w_{1d} \ldots w_{T d}]$
and
![]() $q = [w_{1q} \ldots w_{T q}]$
representing document d and query q, respectively, with T representing the size of the term vocabulary used. The measure of aboutness (topical relevance) is calculated by the standard cosine-similarity (Salton & McGill, Reference Salton and McGill1984):
$q = [w_{1q} \ldots w_{T q}]$
representing document d and query q, respectively, with T representing the size of the term vocabulary used. The measure of aboutness (topical relevance) is calculated by the standard cosine-similarity (Salton & McGill, Reference Salton and McGill1984):
 \begin{equation}{\mathrm{Aboutness}}_{IR}(d,q) = \frac{\sum_{i=1}^{T}(w_{iq}.w_{id})}{\sqrt{\sum_{i=1}^{T} w_{iq}^2 \;.\; \sum_{i=1}^{T} w_{id}^2}}.\end{equation}
\begin{equation}{\mathrm{Aboutness}}_{IR}(d,q) = \frac{\sum_{i=1}^{T}(w_{iq}.w_{id})}{\sqrt{\sum_{i=1}^{T} w_{iq}^2 \;.\; \sum_{i=1}^{T} w_{id}^2}}.\end{equation}
7.1.2. Coverage
The coverage criterion is assessed on the document representation and on the user profile representation. It measures how strongly the user interests are included in a document.
This function produces the maximum value 1 when the non null elements in q ′s vector also belong to d ′s vector. It produces the value zero when the two vectors have no common element. Moreover, the value of the function increases with the increase of the number of common elements.
7.1.3. Appropriateness
This dimension allows to measure how appropriate or how seemly a document is with respect to the user interests.
According to this definition, a piece of information is considered fully appropriate if it covers all the user interests. However, if in addition it covers other subjects, it is considered less appropriate.
7.2. Reformulation in logic
We can consider a user query in IR as the information needed to achieve a goal.
This way, the premise of the goal can be represented by a formula that corresponds to the agent’s information need. Let
![]() $\varphi$
and
$\varphi$
and
![]() $\psi$
be two conjunctions of positive literals of a propositional language. We have:
$\psi$
be two conjunctions of positive literals of a propositional language. We have:
 \begin{eqnarray*} {\mathrm{Aboutness}}_{Logic}(\varphi,\psi)) &=& \frac{|\varphi \cap \psi|}{\sqrt{|\varphi| \;.\; |\psi|}},\\[5pt] {\mathrm{Coverage}}_{Logic}(\varphi,\psi) &=& \frac{|\varphi \cap \psi|}{|\psi|},\\[5pt] {\mathrm{Appropriateness}}_{Logic}(\varphi,\psi) &=& 1 - \frac{|\varphi \setminus \psi| + |\psi \setminus \varphi|}{|L|}.\end{eqnarray*}
\begin{eqnarray*} {\mathrm{Aboutness}}_{Logic}(\varphi,\psi)) &=& \frac{|\varphi \cap \psi|}{\sqrt{|\varphi| \;.\; |\psi|}},\\[5pt] {\mathrm{Coverage}}_{Logic}(\varphi,\psi) &=& \frac{|\varphi \cap \psi|}{|\psi|},\\[5pt] {\mathrm{Appropriateness}}_{Logic}(\varphi,\psi) &=& 1 - \frac{|\varphi \setminus \psi| + |\psi \setminus \varphi|}{|L|}.\end{eqnarray*}
After replacing the premises of the agent’s goal by the formula
![]() $\psi$
, the measure defined in Definition 14 is then re-written as follows:
$\psi$
, the measure defined in Definition 14 is then re-written as follows:
 \begin{align*} U(\varphi,\psi) = \frac{1}{2} \cdot \left(n(\varphi) + \frac{ |\varphi \cap \psi|}{ |\psi| + \frac{|\varphi \setminus \psi|}{|\varphi \setminus \psi | + 1}}\right)\end{align*}
\begin{align*} U(\varphi,\psi) = \frac{1}{2} \cdot \left(n(\varphi) + \frac{ |\varphi \cap \psi|}{ |\psi| + \frac{|\varphi \setminus \psi|}{|\varphi \setminus \psi | + 1}}\right)\end{align*}
with
![]() $n(\varphi) = 1$
if
$n(\varphi) = 1$
if
![]() $\psi \subseteq \varphi$
and
$\psi \subseteq \varphi$
and
![]() $n(\varphi) = 0$
otherwise.
$n(\varphi) = 0$
otherwise.
More precisely, we consider a propositional language L that has T propositional letters
![]() $p_1 \ldots p_{T}$
and a letter
$p_1 \ldots p_{T}$
and a letter
![]() $g_0$
representing the goal of the user. A document d can then be represented by a formula noted
$g_0$
representing the goal of the user. A document d can then be represented by a formula noted
![]() $\varphi_d$
defined as:
$\varphi_d$
defined as:
![]() $\varphi_d = \bigwedge_{i=1, \ldots, T\;and\;w_{i,d}=1} p_i$
. A query q can also be represented by a formula noted
$\varphi_d = \bigwedge_{i=1, \ldots, T\;and\;w_{i,d}=1} p_i$
. A query q can also be represented by a formula noted
![]() $premise(g_0)$
defined by
$premise(g_0)$
defined by
![]() $\psi_q = \bigwedge_{i=1, \ldots, T\;and\;w_{i,q}=1} p_i$
.
$\psi_q = \bigwedge_{i=1, \ldots, T\;and\;w_{i,q}=1} p_i$
.
The following two propositions allows us to, respectively, reformulate in logic the three IR relevance dimensions we have considered from the literature, and to provide some comparisons between the U measure and the IR ones.
Proposition 9
 \begin{align*}{\mathrm{Aboutness}}_{I\; R}(d,q) &= {\mathrm{Aboutness}}_{Logic}(\varphi_d,\psi_q) \\[5pt]{\mathrm{Coverage}}_{I\; R}(d,q) &= {\mathrm{Coverage}}_{Logic}(\varphi_d,\psi_q) \\[5pt]{\mathrm{Appropriateness}}_{I\; R}(d,q) &= {\mathrm{Appropriateness}}_{Logic}(\varphi_d,\psi_q) \end{align*}
\begin{align*}{\mathrm{Aboutness}}_{I\; R}(d,q) &= {\mathrm{Aboutness}}_{Logic}(\varphi_d,\psi_q) \\[5pt]{\mathrm{Coverage}}_{I\; R}(d,q) &= {\mathrm{Coverage}}_{Logic}(\varphi_d,\psi_q) \\[5pt]{\mathrm{Appropriateness}}_{I\; R}(d,q) &= {\mathrm{Appropriateness}}_{Logic}(\varphi_d,\psi_q) \end{align*}
Proposition 10 Let
![]() $\varphi$
and
$\varphi$
and
![]() $\psi$
be two conjunctions of literals.
$\psi$
be two conjunctions of literals.
-
 $U(\varphi,\psi) = {\mathrm{Aboutness}}(\varphi,\psi) = {\mathrm{Appropriateness}}(\varphi,\psi) = 1 \Longleftrightarrow \varphi = \psi$
.
$U(\varphi,\psi) = {\mathrm{Aboutness}}(\varphi,\psi) = {\mathrm{Appropriateness}}(\varphi,\psi) = 1 \Longleftrightarrow \varphi = \psi$
. -
 ${\mathrm{Coverage}}(\varphi,\psi) = 1 \Longleftrightarrow \psi \subseteq \varphi$
.
${\mathrm{Coverage}}(\varphi,\psi) = 1 \Longleftrightarrow \psi \subseteq \varphi$
. -
 $U(\varphi,\psi) = {\mathrm{Aboutness}}(\varphi,\psi) = {\mathrm{Appropriateness}}(\varphi,\psi) ={\mathrm{Coverage}}(\varphi,\psi) = 0 \Longleftrightarrow \varphi \cap \psi = \emptyset$
.
$U(\varphi,\psi) = {\mathrm{Aboutness}}(\varphi,\psi) = {\mathrm{Appropriateness}}(\varphi,\psi) ={\mathrm{Coverage}}(\varphi,\psi) = 0 \Longleftrightarrow \varphi \cap \psi = \emptyset$
. -
 ${\mathrm{Coverage}}(\varphi_1, \psi) \lt {\mathrm{Coverage}}(\varphi_2,\psi) \Longrightarrow U(\varphi_1,\psi) \lt U(\varphi_2,\psi)$
${\mathrm{Coverage}}(\varphi_1, \psi) \lt {\mathrm{Coverage}}(\varphi_2,\psi) \Longrightarrow U(\varphi_1,\psi) \lt U(\varphi_2,\psi)$
-
 ${\mathrm{Appropriateness}}(\varphi_1, \psi) \leq {\mathrm{Appropriateness}}(\varphi_2,\psi)$
and
${\mathrm{Appropriateness}}(\varphi_1, \psi) \leq {\mathrm{Appropriateness}}(\varphi_2,\psi)$
and
 ${\mathrm{Coverage}}(\varphi_1, \psi) = {\mathrm{Coverage}}(\varphi_2,\psi)$
${\mathrm{Coverage}}(\varphi_1, \psi) = {\mathrm{Coverage}}(\varphi_2,\psi)$
 $\Longrightarrow$
$\Longrightarrow$
 $U(\varphi_1,\psi) \leq U(\varphi_2,\psi)$
.
$U(\varphi_1,\psi) \leq U(\varphi_2,\psi)$
.
Example 10 Let us consider again Example 9, with the propositional language whose letters are p, q, r and
![]() $g_0$
.
$g_0$
.
![]() $\psi = p \wedge q$
and let us consider the five formulas:
$\psi = p \wedge q$
and let us consider the five formulas:
![]() $\varphi_1 = r$
,
$\varphi_1 = r$
,
![]() $\varphi_2 = p \wedge r$
,
$\varphi_2 = p \wedge r$
,
![]() $\varphi_3 = p$
,
$\varphi_3 = p$
,
![]() $\varphi_4 = p \wedge q \wedge r$
, and
$\varphi_4 = p \wedge q \wedge r$
, and
![]() $\varphi_5 = p \wedge q$
. The following table summarizes the values of the four measurements.
$\varphi_5 = p \wedge q$
. The following table summarizes the values of the four measurements.

A number of observations emerge from these results. First of all, we notice that two formulas can have identical degrees of coverage without their degrees of usefulness being identical. Thus,
![]() $Coverage(\varphi_2, \psi) = Coverage(\varphi_3, \psi)$
but
$Coverage(\varphi_2, \psi) = Coverage(\varphi_3, \psi)$
but
![]() $U(\varphi_2, \psi) \not= U(\varphi_3, \psi)$
. Similarly, two formulas may have identical degrees of appropriateness without their degrees of usefulness being identical. Thus,
$U(\varphi_2, \psi) \not= U(\varphi_3, \psi)$
. Similarly, two formulas may have identical degrees of appropriateness without their degrees of usefulness being identical. Thus,
![]() $Appropriatemess(\varphi_3, \psi) = Appropriateness(\varphi_4, \psi)$
but
$Appropriatemess(\varphi_3, \psi) = Appropriateness(\varphi_4, \psi)$
but
![]() $U(\varphi_3, \psi) \not= U(\varphi_4, \psi)$
. We also notice that p and
$U(\varphi_3, \psi) \not= U(\varphi_4, \psi)$
. We also notice that p and
![]() $p \wedge q \wedge r$
have identical appropriateness values although for different reasons:
$p \wedge q \wedge r$
have identical appropriateness values although for different reasons:
![]() $appriopriateness(p, p \wedge q) = 2/3$
because p says nothing about q, whereas this is part of the user’s information need, and
$appriopriateness(p, p \wedge q) = 2/3$
because p says nothing about q, whereas this is part of the user’s information need, and
![]() $appriopriateness(p \wedge q \wedge r, p \wedge q) = 2/3$
because
$appriopriateness(p \wedge q \wedge r, p \wedge q) = 2/3$
because
![]() $p \wedge q \wedge r$
, although providing all the information the user need to achieve his/her goal, it provides unnecessary information, r. On the other hand, these different reasons lead to different degrees of usefulness and, in particular,
$p \wedge q \wedge r$
, although providing all the information the user need to achieve his/her goal, it provides unnecessary information, r. On the other hand, these different reasons lead to different degrees of usefulness and, in particular,
![]() $U(p, p \wedge q)$
is much lower than
$U(p, p \wedge q)$
is much lower than
![]() $U(p \wedge q \wedge r, p \wedge q)$
. Indeed, by definition, U favors information that allows the user need to be satisfied (this is fully the case with
$U(p \wedge q \wedge r, p \wedge q)$
. Indeed, by definition, U favors information that allows the user need to be satisfied (this is fully the case with
![]() $p \wedge q \wedge r$
whereas it is partially the case with p). Even if
$p \wedge q \wedge r$
whereas it is partially the case with p). Even if
![]() $p \wedge q \wedge r$
provides unnecessary information, namely r, the user will be able to achieve his/her goal with it, unlike with p.
$p \wedge q \wedge r$
provides unnecessary information, namely r, the user will be able to achieve his/her goal with it, unlike with p.
8. Conclusion and future work
We have proposed an extension of the three definitions of usefulness of information for a cognitive agent proposed in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019). The extension has consisted in considering a more realistic hypothesis, whereby there could be more than one way to achieve a given informative goal. We have then extended the binary approach, which allows to classify a piece of information as being useful or not, and the ordinal approach, which allows to compare two pieces of information in order to establish which one is more useful. Like in Cholvy and da Costa Pereira (Reference Cholvy and da Costa Pereira2019), two different operators have been proposed in this case: a preorder operator and a total order operator. However, neither the binary nor the ordinal approaches allow to take into account unnecessary information when computing the extent to which a piece of information is useful for the user. This is accounted for by the third approach by means of a numerical definition of usefulness which has been inspired by Tversky’s definition of similarity between two objects (Tversky, 1977). We have compared, through an easy to understand example, three IR measures from the literature with our numerical measure. The results of the comparison show that our numerical definition of usefulness, based on the cognitive aspects of the user, allows to capture in a single value different dimensions, without the need for eliciting an explicit priority order on the dimensions from the user. In addition, it allows to somehow account for the serendipity (see Example 8). We agree with Reviglio (Reference Reviglio2019) that there is still room for improvement in addressing the concept of serendipity in disciplines like IR and Recommender Systems. On the other hand, there are many formalisms to represent user’s goals and their generation as well as their updating process (see for example da Costa Pereira & Tettamanzi, Reference da Costa Pereira and Tettamanzi2010; Harland et al., Reference Harland, Morley, Thangarajah and Yorke-Smith2017, Reference Harland, Thangarajah and Yorke-Smith2022), which makes it possible to track the evolution of the achievements of the user’s goal. The formalism we are proposing here can be regarded as a first step toward considering the representation of user’s goals in order to represent the category of serendipity named Illusory by Smets et al. (Reference Smets, Vannieuwenhuyze and Ballon2022). Moreover, our formalism also allows to account for novelty with respect to the user’s beliefs, not only with respect to the past user interactions as usual in the literature (see again Example 8, in which the fact that a piece of information contains information already known by the user diminishes its usefulness).
We believe that in addition to both IR and Search-as-Learning approaches, our usefulness measure can be used in cognitive recommendation systems (Beheshti et al., Reference Beheshti, Yakhchi, Mousaeirad, Ghafari, Goluguri and Edrisi2020) to personalize the items proposed according to the user’s goals, when a representation of the user’s goals is available, or when such representation can be obtained from some learning process (Drachsler et al., Reference Drachsler, Hummel and Koper2009). The framework will then take into account, in addition to the ‘traditional’ user profile, which is built on the basis of the user’s search history, the evolution of the user’s needs (goals) thanks to the calculation of the updated usefulness of the information to be provided to the user. Similarly, our proposed measure could be adapted to Collaborative Filtering approaches for which Parker in his very visionary work (Parker, Reference Parker1995) underlined the interest to take into account holistic profiles instead of history-based search profiles in order to also consider the dynamic aspects of the user’s interests. Another possible application of our work is to adapt/apply our usefulness measure to question-answering systems in order to take into consideration the evolution of the user information needs. Just to cite one example, we plan to adapt and extend the BDI-based framework for conversational agents proposed byWong et al. (2012) with our numerical usefulness measure. The idea is to provide to the user not only an answer which is relevant to his/her question and/or to use the available plans relevant to the question, but also to consider the answer which is more useful with respect to the user’s real needs that is an answer which does not include what he/she already knows. We also plan to consider weighted goals in order to take into account the importance of goals in the definition of information usefulness.
An interesting possible extension of our work could be to take into account the cost or the reliability of the different ways to achieve the goals. Indeed, going back to Example 8 (Section 6), if we consider the current version of our framework, having both p and q will be considered as if one of them were unnecessary information because we have a non deterministic representation of the way to achieve a goal: the usefulness of
![]() $p \wedge q \wedge r$
is
$p \wedge q \wedge r$
is
![]() $\frac{20}{21}$
, that is, slightly less than 1 because it contains information that has become useless with the acquisition of the other (p or q).
$\frac{20}{21}$
, that is, slightly less than 1 because it contains information that has become useless with the acquisition of the other (p or q).
Finally, we would like to notice that we have used propositional logic because for the application to IR, where atoms can be represented as ‘nuggets’, that is a small piece of information that can be considered as a whole, propositional logic is sufficient. An interesting direction could be to extend the formalism to more expressive logic, in order to handle fine-grained representations of information regarding individuals and their relationships.
Aknowledgements
We would like to thank the anonymous reviewers for their careful reading of our manuscript and for their helpful comments and suggestions. Célia da Costa Pereira acknowledges support of the PEPS AIRINFO project funded by the CNRS. This work has been carried out during her visit at the ONERA center of Toulouse.
Competing interests
The authors declare none.