1 Introduction
Intertemporal choices are decisions with outcomes that occur over time; for example, to buy a consumable now or save money for future education, to prepare a proposal soon or delay it until the last minute. Researchers have shown that intertemporal choices are often inconsistent with the economic principles of rationality such as dominance, which is a cornerstone of any normative theory. Relying both on the assumption of monotonicity (i.e., that more money is better) and on the assumption of positive time preferences (i.e., that earlier rewards are better than later ones and later losses are better than earlier ones) (Reference FisherFisher, 1930), in intertemporal choice with money as outcomes, dominance means that if the cumulative money obtained from one option in successive time periods is never less than that obtained from another option, and more is obtained in at least one time period, then the first option is a dominant option and should therefore be preferred (Reference Scholten and ReadScholten & Read, 2014).
Scholten and Read have reported new violations of dominance in which “an intertemporal prospect fares better by making it worse, and fares worse by making it better.” They found that compared with the choice between “A. Receive £75 today vs. B. Receive £100 in 1 year,” the preference for the later and larger (LL) options rather than the sooner and smaller (SS) options was increased given the choices of “C. Receive £75 today and receive £5 in 1 year vs. B. Receive £100 in 1 year” and “A. Receive £75 today vs. D. Pay £5 today and receive £100 in 1 year.” Adding a small delayed reward to an immediate reward (C option) makes the prospect objectively better but decreases the likelihood that the prospect will be chosen; adding an immediate small loss to a delayed reward (D option) makes the prospect objectively worse but increases the attractiveness of the prospect. In addition, when the focal temporal options were changed to losses — i.e., “A’. Pay £75 today vs. B’. Pay £100 in 1 year,” “A’. Pay £75 today vs. D’. Receive £5 today and Pay £100 in 1 year” and “C’. Pay £75 today and pay £5 in 1 year vs. B’. Pay £100 in 1 year” — there was also a preference shift and a violation of the dominance principle. Scholten and Read explained these violations in terms of the account of a preference for improvementFootnote 1, which states a preference for improvement over deterioration (the C and D’ options are deteriorating sequences, whereas the D and C’ options are improving sequences).
Nevertheless, we doubt that a preference for improvement can account for these violations of dominance. The doubt arises from two avenues of research. One avenue of research is concerned with whether the account of a preference for improvement can apply to sequences of unlabeled money, meaning money that is not attributed to a specific origin, such as wage payments or rental income (e.g., Reference Loewenstein and SichermanLoewenstein & Sicherman, 1991). The evidence for a preference for improvement is primarily derived from research on sequences of nonmonetary, qualitative outcomes. For example, in Loewenstein and Prelec’s Example 2, most people preferred visiting an abrasive aunt on one weekend and then visiting friends on the next weekend than the reverse. However, there is no convincing evidence of preferences for improvement in choices between elementary sequences involving money as outcomes (Reference Read and ScholtenRead & Scholten, 2012). Even in Frederick and Loewenstein’s (2008) Study 2a, a preference for deterioration emerged using a matching task involving monetary two-outcome sequences:
G. Receive $2,000 now for signing up as a participant in a 1-year study and receive another $1,000 when the study is complete.
H. Receive $1,000 now for signing up as a participant in a 1-year study and receive another $_____ when the study is complete.
Almost no one gave a response below $2,000, and the mean response was above $2,000.
Given Frederick and Loewenstein’s Study 2a using a match other than a choice task, we conducted a small-scale survey in a classroom with a choice task asking students to choose between “L. Receive CNY 200 in 26 weeks and receive CNY 300 in 52 weeks” and “M. Receive CNY 300 in 26 weeks and receive CNY 200 in 52 weeks,” finding that an overwhelming majority preferred a deteriorated sequence (i.e., option M) to an improved one (i.e., option L).Footnote 2
The other source of doubt arises from our own recent research (Reference Jiang, Hu and ZhuJiang, Hu & Zhu, 2014; Reference Jiang, Sun, Zheng, Wang and QinJiang, Sun, Zheng, Wang & Qin, 2016; Reference Sun and JiangSun & Jiang, 2015). We found some effects in intertemporal choice that might be related to the violations in Reference Scholten and ReadScholten and Read (2014). For example, in Sun and Jiang’s Experiment 3, compared with a choice of “P. Gaining CNY 220 in three weeks vs. Q. Gaining CNY 270 in five weeks,” more people preferred the larger and later (LL) option in the choice of “P’. Gaining CNY 220 in three weeks and losing CNY 21 in six weeks vs. Q’. Gaining CNY 270 in five weeks and losing CNY 27 in six weeks.” Given both that options P’ and Q’ were constructed by adding later losses to options P and Q and that the loss added to option Q was a little larger than that added to option P, the comparison of the Q’ option with the P’ option was objectively worse than the comparison of the Q option with the P option, and therefore the proportion of preference for the Q’ option should be less than the proportion of preference for the Q option. However, the real choice data revealed the reverse trend. The explanation of the preference for improvement cannot account for this effect because options P’ and Q’ were both designed as decreasing sequences and the precipitation speed is even greater in option Q’ (from CNY 270 to –27) than in option P’ (from CNY 220 to –21). We supposed that the effect could be explained by the salience account; that is, introducing extra dated money to simple (one dated-money) options could render the money dimension more salient and cause people to focus and weight money more heavily, therefore, increasing their preference for the LL options in intertemporal rewards.
Moreover, we found that, regardless of whether the extra dated-money was a loss or a gain, inserted before the SS option, inserted between the SS and LL options, or inserted later than the LL options, its introduction reduced intertemporal discounting (Reference Sun and JiangSun & Jiang, 2015). And, the extra dated-money effect can also be extended to intertemporal choice when the focal intertemporal options are losses (Reference Jiang, Sun, Zheng, Wang and QinJiang et al., 2016). Therefore, we suspect that the salience account can also explain Scholten and Read’s violation of dominance because in a choice between one dated-money and a sequence of two dated-money, the sequence is a focal dated-money added with extra dated-money, which could render the money dimension more salient. Thus, we considered that, to produce the violations like Scholten and Read’s, it’s not necessary to construct sequences as they suggested. To extend Scholten and Read’s violations of dominance and examine whether a preference for improvement can account for the violations of dominance, we designed two experiments — Experiment A and Experiment B — using rewards and payments as focal intertemporal option stimuli. In the experiments, the two-outcome money sequences are constructed as deteriorating and objectively worse or improving and objectively better compared with single-dated money options. If the preference for an improving (and objectively better) sequence or the distaste for a deteriorating (and objectively worse) sequence is not obtained, this result will contradict that explanation of a preference for improvement.
1.1 Experiment A
1.2 Method
In Experiment A, 300 students from Zhejiang University of Technology were approached in the library and randomly assigned to one of three conditions — the R (reference) condition, the S+ (improving sequence) and the S− (deteriorating sequence) conditions, which are as follows:
R condition:
U. Receive CNY 200 in 26 weeks
V. Receive CNY 300 in 52 weeks
S+condition:
W. [t]3inReceive CNY 5 in 25 weeks and receive CNY 200 in 26 weeks
V. Receive CNY 300 in 52 weeks
S−condition:
U. Receive CNY 200 in 26 weeks
X. [t]3inReceive CNY 300 in 52 weeks and pay CNY 5 in 53 weeks
The sequence (i.e., option W) in the S+ condition was thus constructed as an improving sequence and the sequence (i.e., option X) in the S− condition was constructed as a deteriorating sequence. The choices were presented in a questionnaire on paper containing other unrelated studies and were listed first to avoid potential contamination by other studies. After completion, each participant received a small gift.
1.3 Results and Discussion
One questionnaire for condition S+ was missed during data collection, leaving 299 participants (143 males, M age = 21.69, SD = 2.56) for the final analysis.
As seen in Figure 1, compared with the choices in R condition, the preference for the SS option in the S+ condition was decreased (from 82% to 48.5%), χ2(1) = 24.67, p < 0.001, ϕ = 0.35, although introducing a small reward (i.e., receive CNY 5 in 25 weeks) to option U (therefore becomes option W) renders the prospect objectively better. In the S− condition, the preference for the LL option was increased compared with the choices in R condition (from 18% to 30%), χ2(1) = 3.95, p = 0.047, ϕ = 0.14, although introducing a small payment (i.e., pay CNY 5 in 53 weeks) to option V (therefore becomes option X) makes the prospect objectively worse. These preference shifts directly contradict the account of a preference for improvement. The sequence in S+ condition was constructed as improving and therefore should be preferred according to a preference for improvement; whereas the sequence in the S− condition was constructed as a deteriorating sequence and thus should be disfavored.
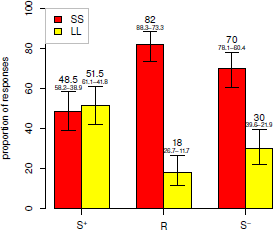
Figure 1. Proportion of responses (%) in the S+, R and S− conditions in Experiment A. Numbers with dashes are 95% confidence intervals.
2 Experiment B
In Experiment B, we substituted rewards of focal intertemporal options with payments.
2.1 Method
Another 300 students from Zhejiang University of Technology participated in this experiment. The data were collected in the library’s study room. Each subject was randomly assigned to one of three conditions—the R (reference) condition, the S+(improving sequence) and the S− (deteriorating sequence) conditions, which are as follows:
R condition:
U’. Pay CNY 200 in 26 weeks
V’. Pay CNY 300 in 52 weeks
S+condition:
U’. Pay CNY 200 in 26 weeks
W’. [t]2.8inPay CNY 300 in 52 weeks and receive CNY 5 in 53 weeks
S−condition:
X’. Pay CNY 5 in 25weeks and pay CNY 200 in 26 weeks
V’. Pay CNY 300 in 52 weeks
The sequence (i.e., option W’) in the S+ condition was thus constructed as an improving sequence and the sequence (i.e., option X’) in the S− condition was constructed as a deteriorating sequence. The choices were presented in a questionnaire on paper with other unrelated studies and were listed as the first problems. After completing the questionnaire, each participant received a small gift.
2.2 Results and Discussion
Two questionnaires for condition R were missed during data collection, and one participant in condition S− did not respond to the intertemporal choice, leaving 297 participants (142 males, M age = 20.88, SD = 2.1) for the final analysis.
As demonstrated in Figure 2, compared with the choices in R condition, the preference for the LL option was decreased (from 43.9% to 32%) in the S+ condition, χ2(1) = 2.97, p = 0.085, ϕ = 0.12, although introducing a small reward (i.e., receive CNY 5 in 53 weeks) to option V’ (therefore becomes option W’) makes the prospect objectively better. In the S− condition, the preference for the SS option was increased compared with the choices in R condition (from 56.1% to 70.7%), χ2(1) = 4.52, p = 0.034, ϕ = 0.15, although introducing a small payment (i.e., pay CNY 5 in 25 weeks) to option U’ (therefore becomes option X’) makes the prospect objectively worse. These preference shifts are inconsistent with the predictions of a preference for improvement. The sequence in S+condition was constructed as improving and therefore should be preferred, and the sequence in the S− condition was constructed as a deteriorating sequence and thus should be disfavored.
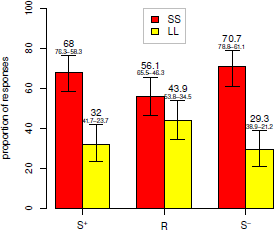
Figure 2. Proportion of responses (%) in the S+, R and S− conditions in Experiment B. Numbers with dashes are 95% confidence intervals.
3 General Discussion
In this study, we reexamined the violations of dominance discovered by Reference Scholten and ReadScholten and Read (2014) and found that the intertemporal options designed to produce these violations do not necessarily conform to the principles of a preference for improvement (Reference Loewenstein and PrelecLoewenstein & Prelec, 1993). The sequences in this study that were constructed to be objectively better and to improve (“Receive CNY 5 in 25 weeks and receive CNY 200 in 26 weeks” in Experiment A and “Pay CNY 300 in 52 weeks and receive CNY 5 in 53 weeks” in Experiment B) had reduced preferences. The sequences that were constructed to be objectively worse and to deteriorate (“Receive CNY 300 in 52 weeks and pay CNY 5 in 53 weeks” in Experiment A and “Pay CNY 5 in 25 weeks and pay CNY 200 in 26 weeks” in Experiment B) had increased preferences.
Earlier, in the introduction, we suggested that the salience account may explain Scholten and Read’s violations of dominance, which was one of the reasons that we designed the current study. Although the results reported here are consistent with the salience account’s predictions that extra-dated money makes the money dimension more salient and more heavily weighted, thus reducing intertemporal discounting (Reference Jiang, Hu and ZhuJiang et al., 2014; Reference Jiang, Sun, Zheng, Wang and QinJiang et al., 2016; Reference Sun and JiangSun & Jiang, 2015), we did not examine this account directly. The main purpose of this paper was to extend Scholten and Read’s violations and to provide possible evidence against the explanation of a preference for improvement. An alternative hypothesis to the salience account that the money dimension weights differently for the sequences conditions vs. the one dated-outcome conditions is that utilities change. Recently, multiple studies have suggested that, when making intertemporal choices, people adopt attribute-based approaches such as comparing difference between outcomes of pairwise options with that of delays (Reference Dai and BusemeyerDai & Busemeyer, 2014; Reference Ericson, White, Laibson and CohenEricson, White, Laibson & Cohen, 2015; Reference Jiang, Liu, Cai and LiJiang, Liu, Cai & Li, 2016; Reference Scholten and ReadScholten & Read, 2010). For example, when choosing between “Receive CNY 200 in 26 weeks” and “Receive CNY 300 in 52 weeks,” people compare the difference between “Receive CNY 200” and “Receive CNY 300” with the difference between “26 weeks Delayed” and “52 weeks Delayed.” The utility-changing hypothesis argues that the comparison between outcomes seems larger when a small outcome is introduced; for example, the presence of CNY 5 makes the comparison of “Receive CNY 200” and “Receive CNY 300” seem larger. This hypothesis is similar to the evaluability hypothesis proposed by Reference Bateman, Dent, Peters, Slovic and StarmerBateman, Dent, Peters, Slovic and Starmer (2007) to explain why the attractiveness of playing a simple game (7/36 to win $9; otherwise win nothing) is greatly increased by introducing a small loss (7/36 win $9; otherwise lose 5¢). Bateman et al. proposed that in the second game, comparison with the small loss makes $9 more valued, thus increasing the gamble’s attractiveness. However, the utility changing hypothesis is confined to the findings reported here and cannot accommodate the findings of Jiang et al. (2014), Reference Sun and JiangSun and Jiang (2015) and Jiang et al. (2016), because some of the extra-dated money introduced in their studies is rather large; for example, a common “Gain CNY 4250 now” was added to both of the pairwise options of “Gain CNY 4800 in a year” and “Gain CNY 8000 in 4 years” (in Experiment 1A, Jiang et al., 2014).
Recently, several sequence effects, which are when single-dated outcomes are expanded into sequences of two outcomes, choice results are contradictory to the predictions of the exponentially-discounted modelFootnote 3, have been discovered by researchers (Jiang, et al, 2014; Reference Jiang, Sun, Zheng, Wang and QinJiang et al. 2016; Reference Magen, Dweck and GrossMagen, Dweck & Gross, 2008; Reference Rao and LiRao & Li, 2011; Reference Read, Olivola and HardistyRead, Olivola & Hardisty, in press; Reference Read and ScholtenRead & Scholten, 2012; Reference Scholten and ReadScholten & Read, 2014; Reference Sun and JiangSun & Jiang, 2015; Reference Urminsky and KivetzUrminsky & Kivetz, 2011; Reference Wu and HeWu & He, 2012). The salience account was proposed to explain the decreased discounting rate when a common money amount was added to both single-outcome SS and LL options (Reference Jiang, Hu and ZhuJiang et al., 2014; Reference Jiang, Sun, Zheng, Wang and QinJiang et al., 2016; Reference Sun and JiangSun & Jiang, 2015), and was also suggested to explain the effects reported here. We should point out that, in these studies, the amount added was smaller than outcomes of SS options. When the amount is larger than outcomes of SS options or is zero, other factors may kick in and make the salience effect trivial (e.g., Read et al., in press; Reference Read and ScholtenRead & Scholten, 2012). The Appendix summarizes whether different sequence effects can be accommodated by alternative models; it extends a similar summary by Reference Scholten, Read and SanbornScholten, Read & Sanborn (2016).
It can be noted that the timing of SS options delivered in our study (in 26 weeks) is somewhat different from that in Scholten and Read’s study, in which SS options were delivered immediately (today). The reason that the timing was designed in this manner, instead of in the manner of Scholten and Read, is that to construct choice stimuli in this study, such as “Receive CNY 5 in 25 weeks and receive CNY 200 in 26 weeks” (which should be objectively better and improving), the SS option (“Receive CNY 200 in 26 weeks”) must be delayed instead of delivered now. However, the sequence structure was retained (Reference Loewenstein and PrelecLoewenstein & Prelec, 1993). Furthermore, in the current study we cannot describe the proportions of participants who were affected by the manipulation and exhibited a violation, for we did not use the same subjects across conditions. Further studies identifying the source of the individual differences would be more helpful to understand the nature of this violation of dominance.
4 Conclusions
We found the extensions of Reference Scholten and ReadScholten and Read (2014)’s violations of dominance. That is, sequences that were constructed to be objectively better and to improve returned reduced preferences, whereas sequences that were constructed to be objectively worse and to deteriorate returned increased preferences. These violations contradict the predictions of a preference for improvement originally proposed by Scholten and Read to explain their violations.
Appendix: Whether Sequence Effects Can Be Accommodated by the Sequences Model (SM), the Trade off Model (TM), or the Salience Account (SA)?

a t E can be before t S, between t S and t L, or after t L. When t E is between t S and t L, extra-dated money effect becomes common-consequence effect. b x E has a same sign with x S and x L. c x E has a different sign with x S and x L. d x T has a same sign with x S and x L. e x T has a different sign with x S and x L. f x V has a same sign with x S and x L. g x V has a different sign with x S and x L.
Note 1. Utility functions for SM and TM are assumed to be concave over gains and convex over losses, which is common in our field (Reference Kahneman and TverskyKahneman & Tversky, 1979; Reference Loewenstein and PrelecLoewenstein & Prelec, 1992).
Note 2. One model that holds the instantaneous utilities of the outcomes in a sequence are discounted as a function of their delays and summed as a discounted utility of the sequence (Reference Scholten, Read and SanbornScholten et al., 2016) is not included in the table, because it cannot accommodate most of the sequence effects listed here, except for the reverse front-end amount effect and the relocation effect.
Note 3. SM allows for both preferences for improvement and spreading and the opposite preferences. If we allow SM to accommodate some sequence effects, we should assume preferences for improvement and spreading, however, on the other way, if we allow it to accommodate some other sequence effects, we should assume the opposite preferences. Therefore, we hold the preferences for improvement and spreading as priors for SM, because the empirical results in Reference Loewenstein and PrelecLoewenstein and Prelec (1993) suggested so.
Note 4. SA is a qualitative rather than a quantitative model at present, which generally assumes that outcomes in sequences, relative to delays, are more weighted compares with single dated outcomes relative to delays, therefore less discounting is in a choice of sequences than in a choice of single dated outcomes. If more assumptions, such as that a utility function is concave over gains, is allowed into SA, more sequence effects can be accommodated.






