Hostname: page-component-77c89778f8-vpsfw Total loading time: 0 Render date: 2024-07-18T22:46:43.909Z Has data issue: false hasContentIssue false
  • English
  • Français

SIEVES AND THE MINIMAL RAMIFICATION PROBLEM

Published online by Cambridge University Press:  18 June 2018

Lior Bary-Soroker  and
Tomer M. Schlank
Lior Bary-Soroker
Affiliation:
Tel Aviv University, School of Mathematical Sciences, Israel (barylior@post.tau.ac.il)
Tomer M. Schlank
Affiliation:
The Hebrew University, Einstein Institute of Mathematics, Israel (tomer.schlank@mail.huji.ac.il)
Get access Rights & Permissions [Opens in a new window]

Abstract

The minimal ramification problem may be considered as a quantitative version of the inverse Galois problem. For a nontrivial finite group 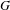$G$, let 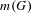$m(G)$ be the minimal integer $m$ for which there exists a 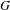$G$-Galois extension 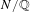$N/\mathbb{Q}$ that is ramified at exactly $m$ primes (including the infinite one). So, the problem is to compute or to bound 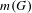$m(G)$.

In this paper, we bound the ramification of extensions 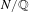$N/\mathbb{Q}$ obtained as a specialization of a branched covering 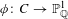$\unicode[STIX]{x1D719}:C\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$. This leads to novel upper bounds on 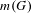$m(G)$, for finite groups 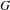$G$ that are realizable as the Galois group of a branched covering. Some instances of our general results are:

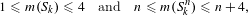$$\begin{eqnarray}1\leqslant m(S_{k})\leqslant 4\quad \text{and}\quad n\leqslant m(S_{k}^{n})\leqslant n+4,\end{eqnarray}$$
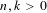for all $n,k>0$. Here 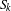$S_{k}$ denotes the symmetric group on 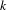$k$ letters, and 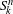$S_{k}^{n}$ is the direct product of $n$ copies of 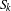$S_{k}$. We also get the correct asymptotic of 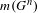$m(G^{n})$, as 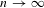$n\rightarrow \infty$ for a certain class of groups 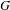$G$.

Our methods are based on sieve theory results, in particular on the Green–Tao–Ziegler theorem on prime values of linear forms in two variables, on the theory of specialization in arithmetic geometry, and on finite group theory.

Keywords

Hilbert’s irreducibility theoreminverse Galois problemspecializationsramification
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 3 , May 2020 , pp. 919 - 945
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beckmann, S., On extensions of number fields obtained by specializing branched coverings, J. Reine Angew. Math. 419 (1991), 27–53.Google Scholar
Boston, N. and Markin, N., The fewest primes ramified in a G-extension of ℚ, Ann. Sci. Math. Québec 33(2) (2009), 145–154.Google Scholar
De Witt, M., Minimal ramification and the inverse Galois problem over the rational function field 𝔽p(t), J. Number Theory 143 (2014), 62–81.Google Scholar
Fried, M. D. and Jarden, M., Field Arithmetic, 3rd edn, Revised by Jarden, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], Volume 11 (Springer, Berlin, 2008).Google Scholar
Green, B., Pop, F. and Roquette, P., On Rumely’s local-global principle, Jahresber. Dtsch. Math.-Ver. 97(2) (1995), 43–74.Google Scholar
Green, B. and Tao, T., Linear equations in primes, Ann. of Math. (2) 171(3) (2010), 1753–1850.10.4007/annals.2010.171.1753Google Scholar
Green, B. and Tao, T., The Möbius function is strongly orthogonal to nilsequences, Ann. of Math. (2) 175(2) (2012), 541–566.Google Scholar
Green, B., Tao, T. and Ziegler, T., An inverse theorem for the Gowers U s+1[N]-norm, Ann. of Math. (2) 176(2) (2012), 1231–1372.Google Scholar
Halberstam, H. and Richert, H.-E., Sieve Methods, London Mathematical Society Monographs, Volume 4 (Academic Press [A subsidiary of Harcourt Brace Jovanovich, Publishers], London-New York, 1974).Google Scholar
Harbater, D., Abhyankar’s conjecture on Galois groups over curves, Invent. Math. 117(1) (1994), 1–25.Google Scholar
Harpaz, Y., Skorobogatov, A. N. and Wittenberg, O., The Hardy-Littlewood conjecture and rational points, Compositio Mathematica 150(12) (2014), 2095–2111.Google Scholar
Hoelscher, J. L., Galois extensions ramified only at one prime, J. Number Theory 129(2) (2009), 418–427.Google Scholar
Jones, J. W. and Roberts, D. P., Number fields ramified at one prime, in Algorithmic Number Theory, Vol. 5011, Lecture Notes in Computational Science, pp. 226–239 (Springer, Berlin, 2008).Google Scholar
Khare, C., Larsen, M. and Savin, G., Functoriality and the inverse Galois problem, Compos. Math. 144(3) (2008), 541–564.Google Scholar
Kisilevsky, H., Neftin, D. and Sonn, J., On the minimal ramification problem for semiabelian groups, Algebra Number Theory 4(8) (2010), 1077–1090.10.2140/ant.2010.4.1077Google Scholar
Kisilevsky, H. and Sonn, J., On the minimal ramification problem for ℓ-groups, Compos. Math. 146(3) (2010), 599–606.10.1112/S0010437X10004719Google Scholar
Legrand, F., Specialization results and ramification conditions, Israel Journal of Mathematics 214(2) (2016), 621–650.10.1007/s11856-016-1349-yGoogle Scholar
Malle, G. and Heinrich Matzat, B., Inverse Galois Theory, Springer Monographs in Mathematics (Springer, Berlin, 1999).10.1007/978-3-662-12123-8Google Scholar
Malle, G. and Roberts, D. P., Number fields with discriminant ± 2a3b and Galois group A n or S n, LMS J. Comput. Math. 8 (2005), 80–101 (electronic).10.1112/S1461157000000905Google Scholar
Markin, N. and Ullom, S. V., Minimal ramification in nilpotent extensions, Pacific J. Math. 253(1) (2011), 125–143.Google Scholar
Milne, J. S., Étale Cohomology, Princeton Mathematical Series, Volume 33 (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields, 2nd edn, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Volume 323 (Springer, Berlin, 2008).Google Scholar
Nomura, A., Notes on the minimal number of ramified primes in some l-extensions of Q, Arch. Math. (Basel) 90(6) (2008), 501–510.Google Scholar
Plans, B., On the minimal number of ramified primes in some solvable extensions of ℚ, Pacific J. Math. 215(2) (2004), 381–391.Google Scholar
Raynaud, M., Revêtements de la droite affine en caractéristique p > 0 et conjecture d’Abhyankar, Invent. Math. 116(1–3) (1994), 425–462.10.1007/BF01231568+0+et+conjecture+d’Abhyankar,+Invent.+Math.+116(1–3)+(1994),+425–462.10.1007/BF01231568>Google Scholar
Serre, J.-P., Topics in Galois Theory, 2nd edn, Research Notes in Mathematics, (A K Peters, Ltd., 2008).Google Scholar
The Stacks Project Authors. stacks project. http://stacks.math.columbia.edu, 2015.Google Scholar
Völklein, H., Groups as Galois Groups, An Introduction, Cambridge Studies in Advanced Mathematics, Volume 53 (Cambridge University Press, Cambridge, 1996).Google Scholar
Wiese, G., On projective linear groups over finite fields as Galois groups over the rational numbers, in Modular Forms on Schiermonnikoog, pp. 343–350 (Cambridge University Press, Cambridge, 2008).Google Scholar
Zywina, D., The inverse Galois problem for PSL2(𝔽p), Duke Mathematical Journal 164(12) (2015), 2253–2292.Google Scholar