Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-28T05:57:41.864Z Has data issue: false hasContentIssue false
  • English
  • Français

OPTIMAL GEVREY STABILITY OF HYDROSTATIC APPROXIMATION FOR THE NAVIER-STOKES EQUATIONS IN A THIN DOMAIN

Part of: Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  06 September 2023

Chao Wang  and
Yuxi Wang Open the ORCID record for Yuxi Wang [Opens in a new window]
Chao Wang
Affiliation:
School of Mathematical Sciences, Peking University, Beijing 100871, China (wangchao@math.pku.edu.cn)
Yuxi Wang*
Affiliation:
School of Mathematics, Sichuan University, Chengdu 610064, China
*
wangyuxi@scu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the hydrostatic approximation for the Navier-Stokes system in a thin domain. When we have convex initial data with Gevrey regularity of optimal index 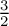$\frac {3}{2}$ in the x variable and Sobolev regularity in the y variable, we justify the limit from the anisotropic Navier-Stokes system to the hydrostatic Navier-Stokes/Prandtl system. Due to our method in the paper being independent of 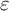$\varepsilon $, by the same argument, we also obtain the well-posedness of the hydrostatic Navier-Stokes/Prandtl system in the optimal Gevrey space. Our results improve upon the Gevrey index of 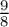$\frac {9}{8}$ found in [15, 35].

Keywords

Navier-Stokes equationshydrostatic approximationthin domain

MSC classification

Primary: 35Q30: Navier-Stokes equations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , First View , pp. 1 - 46
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexandre, R., Wang, Y., Xu, C.-J. and Yang, T., Well-posedness of the Prandtl Equation in Sobolev Spaces, J. Amer. Math. Soc. 28 (2015), 745–784.CrossRefGoogle Scholar
Bahouri, H., Chemin, J. Y. and Danchin, R., Fourier Analysis and Nonlinear Partial Differential Equations (Grundlehren der mathematischen Wissenschaften) vol. 343 (Springer-Verlag Berlin Heidelberg, 2011).CrossRefGoogle Scholar
Brenier, Y., Homogeneous hydrostatic flows with convex velocity profiles, Nonlinearity 12(3) (1999), 495–512.CrossRefGoogle Scholar
Brenier, Y., Remarks on the derivation of the hydrostatic Euler equations, Bull. Sci. Math. 127(7) (2003), 585–595.CrossRefGoogle Scholar
Cao, C., Ibrahim, S., Nakanishi, K. and Titi, E., Finite-time blowup for the inviscid Primitive equations of oceanic and atmospheric dynamics, Comm. Math. Phys. 337(2) (2015), 473–482.CrossRefGoogle Scholar
Chen, D., Wang, Y. and Zhang, Z., Well-posedness of the linearized Prandtl equation around a nonmonotonic shear flow, Ann. Inst. H. Poincare Anal. Non Lineaire 35 (2018), 1119–1142.CrossRefGoogle Scholar
Chen, Q., Wu, D. and Zhang, Z., On the ${L}^{\infty }$ stability of Prandtl expansions in Gevrey class, Sci. China Math. 65 (2022), 2521—2562.CrossRefGoogle Scholar
Dietert, H. and Gérard-Varet, , Well-posedness of the Prandtl equation without any structural assumption, Ann. PDE 5 (2019), 1–51.CrossRefGoogle Scholar
Fei, M., Tao, T. and Zhang, Z., On the zero-viscosity limit of the Navier-Stokes equations in R3+ without analyticity, J. Math. Pures Appl. 112(9) (2018), 170–229.CrossRefGoogle Scholar
Gérard-Varet, D. and Dormy, E., On the ill-posedness of the Prandtl equation, J. Amer. Math. Soc. 23 (2010), 591–609.CrossRefGoogle Scholar
Gérard-Varet, D., Iyer, S. and Maekawa, Y., Improved well-posedness for the Triple-Deck and related models via concavity, Preprint, arXiv:2205.15829.Google Scholar
Gérard-Varet, D., Maekawa, Y. and Masmoudi, N., Gevrey stability of Prandtl expansions for 2-dimensional Navier-Stokes flows, Duke Math. J. 167 (2018), 2531–2631.CrossRefGoogle Scholar
Gérard-Varet, D., Maekawa, Y. and Masmoudi, N., Optimal Prandtl expansion around concave boundary layer, Preprint, arXiv:2005.05022.Google Scholar
Gérard-Varet, D. and Masmoudi, N., Well-posedness for the Prandtl system without analyticity or monotonicity, Ann. Sci. Ec. Norm. Super. 48 (2015), 1273–1325.CrossRefGoogle Scholar
Gérard-Varet, D., Masmoudi, N. and Vicol, V., Well-posedness of the hydrostatic Navier-Stokes equations, Anal. PDE 13 (2020), 1417–1455.CrossRefGoogle Scholar
Grenier, E., On the derivation of homogeneous hydrostatic equations, . M2AN Math Model. Numer. Anal. 33(5) (1999), 965–970.CrossRefGoogle Scholar
Grenier, E., Guo, Y. and Nguyen, T., Spectral instability of general symmetric shear flows in a two-dimensional channel, Adv. Math. 292 (2016), 52–110.CrossRefGoogle Scholar
Grenier, E. and Nguyen, T., ${L}^{\infty }$ instability of Prandtl layers, Ann. PDE 5 (2019), 1–36.CrossRefGoogle Scholar
Kukavica, I., Masmoudi, N., Vicol, V. and Wong, T., On the local well-posedness of the Prandtl and the hydrostatic Euler equations with multiple monotonicity regions, SIAM J. Math. Anal. 46(6) (2014), 3865–3890.CrossRefGoogle Scholar
Kukavica, I., Temam, R., Vicol, V. and Ziane, M., Local existence and uniqueness for the hydrostatic Euler equations on a bounded domain, J. Differential Equations 250(3) (2011), 1719–1746.CrossRefGoogle Scholar
Kukavica, I., Vicol, V. and Wang, F., The inviscid limit for the Navier-Stokes equations with data analytic only near the boundary. Arch. Ration. Mech. Anal. 237 (2020), 779–827.CrossRefGoogle Scholar
Lagrée, P.-Y. and Lorthois, S., The RNS/Prandtl equations and their link with other asymptotic descriptions: application to the wall shear stress scaling in a constricted pipe, Int. J. Eng. Sci. 43 (2005), 352–378.CrossRefGoogle Scholar
Li, W. and Yang, T., Well-posedness in Gevrey space for the Prandtl equations with non-degenerate critical points, J. Eur. Math. Soc. 22 (2020), 717–775.CrossRefGoogle Scholar
Lombardo, M. C., Cannone, M. and Sammartino, M., Well-posedness of the boundary layer equations, SIAM J. Math. Anal. 35 (2003), 987–1004.CrossRefGoogle Scholar
Maekawa, Y., On the inviscid limit problem of the vorticity equations for viscous incompressible flows in the half-plane, Comm. Pure Appl. Math. 67 (2014), 1045–1128.CrossRefGoogle Scholar
Masmoudi, N. and Wong, T., On the ${H}^s$ theory of hydrostatic Euler equations, Arch. Ration. Mech. Anal. 204(1) (2012), 231–271.CrossRefGoogle Scholar
Masmoudi, N. and Wong, T., Local-in-time existence and uniqueness of solutions to the Prandtl equations by energy methods, Comm. Pure Appl. Math. 68 (2015), 1683–1741.CrossRefGoogle Scholar
Nguyen, T. and Nguyen, T., The inviscid limit of Navier-Stokes equations for analytic data on the halfspace, Arch. Ration. Mech. Anal. 230 (2018), 1103–1129.CrossRefGoogle Scholar
Oleinik, O., On the mathematical theory of boundary layer for an unsteady flow of incompressible fluid, J. Appl. Math. Mech. 30 (1966), 951–974.CrossRefGoogle Scholar
Paicu, M., Zhang, P. and Zhang, Z., On the hydrostatic approximate of the Navier-Stokes equations in a thin strip, Adv. Math. 372 (2020), 1–42.CrossRefGoogle Scholar
Renardy, M., Ill-posedness of the hydrostatic Euler and Navier-Stokes equations, Arch. Ration. Mech. Anal. 194 (2009), 877–886.CrossRefGoogle Scholar
Sammartino, M. and Caflisch, R. E., Zero viscosity limit for analytic solutions of the Navier-Stokes equation on a half-space. I. Existence for Euler and Prandtl equations, Comm. Math. Phys. 192 (1998), 433–461.CrossRefGoogle Scholar
Sammartino, M. and Caflisch, R. E., Zero viscosity limit for analytic solutions of the Navier-Stokes equation on a half-space. II. Construction of the Navier-Stokes solution, Comm. Math. Phys. 192 (1998), 463–491.CrossRefGoogle Scholar
Wang, C., Wang, Y. and Zhang, Z., Zero-viscosity limit of the Navier-Stokes equations in the analytic setting, Arch. Ration. Mech. Anal. 224 (2017), 555–595.CrossRefGoogle Scholar
Wang, C., Wang, Y. and Zhang, Z., Gevrey stability of hydrostatic approximate for the Navier-Stokes equations in a thin domain, Nonlinearity 34 (2021), 7185–7226.CrossRefGoogle Scholar
Wang, L., Xin, Z. and Zang, A., Vanishing viscous limits for 3D Navier-Stokes equations with a Navier slip boundary condition, J. Math. Fluid Mech. 14 (2012), 791–825.CrossRefGoogle Scholar
Wang, X., A Kato type theorem on zero viscosity limit of Navier-Stokes flows, Indiana Univ. Math. J. 50 (2001), 223–241.CrossRefGoogle Scholar
Wong, T., Blowup of solutions of the hydrostatic Euler equations, Proc. Amer. Math. Soc. 143(3) (2015), 1119–1125.CrossRefGoogle Scholar
Xiao, Y. and Xin, Z., On the vanishing viscosity limit for the 3D Navier-Stokes equations with a slip boundary condition, Comm. Pure Appl. Math. 60 (2007), 1027–1055.CrossRefGoogle Scholar
Xin, Z. and Zhang, L., On the global existence of solutions to the Prandtl system, Adv. Math. 181 (2004), 88–133.CrossRefGoogle Scholar