Hostname: page-component-77c89778f8-m42fx Total loading time: 0 Render date: 2024-07-17T17:51:13.301Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE EXCEPTIONAL SPECIALIZATIONS OF BIG HEEGNER POINTS

Part of: Arithmetic algebraic geometry

Published online by Cambridge University Press:  04 February 2016

Francesc Castella
Francesc Castella*
Affiliation:
Department of Mathematics, UCLA, Math Sciences Building, Los Angeles, CA 90095, USA (castella@math.ucla.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend the 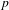$p$-adic Gross–Zagier formula of Bertolini et al. [Generalized Heegner cycles and 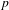$p$-adic Rankin $L$-series, Duke Math. J.162(6) (2013), 1033–1148] to the semistable non-crystalline setting, and combine it with our previous work [Castella, On the 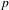$p$-adic variation of Heegner points, Preprint, 2014, arXiv:1410.6591] to obtain a derivative formula for the specializations of Howard’s big Heegner points [Howard, Variation of Heegner points in Hida families, Invent. Math.167(1) (2007), 91–128] at exceptional primes in the Hida family.

Keywords

Hida familiesHeegner pointsp-adic L-functionsL-invariants

MSC classification

Primary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Secondary: 11G35: Varieties over global fields 11G15: Complex multiplication and moduli of abelian varieties 11G05: Elliptic curves over global fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 1 , February 2018 , pp. 207 - 240
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertolini, M., Darmon, H. and Prasanna, K., Generalized Heegner cycles and p-adic Rankin L-series, Duke Math. J. 162(6) (2013), 1033–1148.Google Scholar
Castella, F., Heegner cycles and higher weight specializations of big Heegner points, Math. Ann. 356(4) (2013), 1247–1282.Google Scholar
Castella, F., On the $p$ -adic variation of Heegner points, Preprint, 2014,arXiv:1410.6591.Google Scholar
Castella, F., $p$ -adic heights of Heegner points and Beilinson–Flach elements, Preprint, 2015, arXiv:1509.02761.Google Scholar
Coleman, R. F., Reciprocity laws on curves, Compos. Math. 72(2) (1989), 205–235.Google Scholar
Coleman, R. F., A p-adic Shimura isomorphism and p-adic periods of modular forms, in p-adic Monodromy and the Birch and Swinnerton–Dyer Conjecture (Boston, MA, 1991), Contemporary Mathematics, Volume 165, pp. 21–51 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Coleman, R. F., Classical and overconvergent modular forms, Invent. Math. 124(1–3) (1996), 215–241.Google Scholar
Coleman, R. and Iovita, A., Hidden structures on semistable curves, Astérisque 331 (2010), 179–254.Google Scholar
Ferrero, B. and Greenberg, R., On the behavior of p-adic L-functions at s = 0, Invent. Math. 50(1) (1978/79), 91–102.Google Scholar
Greenberg, R., Trivial zeros of p-adic L-functions, in p-adic Monodromy and the Birch and Swinnerton–Dyer Conjecture (Boston, MA, 1991), Contemporary Mathematics, Volume 165, pp. 149–174 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Greenberg, R. and Stevens, G., p-adic L-functions and p-adic periods of modular forms, Invent. Math. 111(2) (1993), 407–447.Google Scholar
Gross, B. H. and Koblitz, N., Gauss sums and the p-adic 𝛤-function, Ann. of Math. (2) 109(3) (1979), 569–581.Google Scholar
Hida, H., Galois representations into GL2(Z p ⟦X⟧) attached to ordinary cusp forms, Invent. Math. 85(3) (1986), 545–613.CrossRefGoogle Scholar
Howard, B., Central derivatives of L-functions in Hida families, Math. Ann. 339(4) (2007), 803–818.Google Scholar
Howard, B., Variation of Heegner points in Hida families, Invent. Math. 167(1) (2007), 91–128.Google Scholar
Hyodo, O. and Kato, K., Semi-stable reduction and crystalline cohomology with logarithmic poles, Astérisque 223 (1994), 221–268. Périodes $p$ -adiques (Bures-sur-Yvette, 1988).Google Scholar
Iovita, A. and Spieß, M., Derivatives of p-adic L-functions, Heegner cycles and monodromy modules attached to modular forms, Invent. Math. 154(2) (2003), 333–384.Google Scholar
Katz, N. M., p-adic properties of modular schemes and modular forms, in Modular Functions of One Variable, III (Proceedings of Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Mathematics, Volume 350, pp. 69–190 (Springer, Berlin, 1973).Google Scholar
Kings, G., Loeffler, D. and Zerbes, S., Rankin–Eisenstein classes and explicit reciprocity laws, Preprint, 2015, arXiv:1503.02888.Google Scholar
Lei, A., Loeffler, D. and Zerbes, S. L., Euler systems for Rankin–Selberg convolutions of modular forms, Ann. of Math. (2) 180(2) (2014), 653–771.Google Scholar
Mazur, B., Tate, J. and Teitelbaum, J., On p-adic analogues of the conjectures of Birch and Swinnerton–Dyer, Invent. Math. 84(1) (1986), 1–48.Google Scholar
Nekovář, J., p-adic Abel-Jacobi maps and p-adic heights, in The Arithmetic and Geometry of Algebraic Cycles (Banff, AB, 1998), CRM Proceedings Lecture Notes, Volume 24, pp. 367–379 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Nekovář, J., Selmer complexes, Astérisque 310 (2006), viii+559.Google Scholar
Nekovář, J. and Plater, A., On the parity of ranks of Selmer groups, Asian J. Math. 4(2) (2000), 437–497.Google Scholar
Ochiai, T., A generalization of the Coleman map for Hida deformations, Amer. J. Math. 125(4) (2003), 849–892.Google Scholar
Ohta, M., On the p-adic Eichler–Shimura isomorphism for 𝛬-adic cusp forms, J. Reine Angew. Math. 463 (1995), 49–98.Google Scholar
Ohta, M., Ordinary p-adic étale cohomology groups attached to towers of elliptic modular curves. II, Math. Ann. 318(3) (2000), 557–583.CrossRefGoogle Scholar
Perrin-Riou, B., p-adic L-functions and p-adic Representations, SMF/AMS Texts and Monographs, Volume 3 (American Mathematical Society, Providence, RI, 2000). Translated from the 1995 French original by Leila Schneps and revised by the author.Google Scholar
Rubin, K., Euler Systems, Annals of Mathematics Studies, Volume 147 (Princeton University Press, Princeton, NJ, 2000). Hermann Weyl Lectures. The Institute for Advanced Study.Google Scholar
Serre, J.-P., Formes modulaires et fonctions zêta p-adiques, in Modular Functions of One Variable, III (Proc. Internat. Summer School, Univ. Antwerp, 1972), Lecture Notes in Mathematics, Volume 350, pp. 191–268 (Springer, Berlin, 1973).Google Scholar
Venerucci, R., Exceptional zero formulae and a conjecture of Perrin-Riou, Invent. Math. (2015), to appear.Google Scholar
Wiles, A., On ordinary 𝜆-adic representations associated to modular forms, Invent. Math. 94(3) (1988), 529–573.Google Scholar