No CrossRef data available.
Article contents
A DERIVED LAGRANGIAN FIBRATION ON THE DERIVED CRITICAL LOCUS
Part of:
Algebraic geometry: Foundations
Categories and geometry
Symplectic geometry, contact geometry
Published online by Cambridge University Press: 31 August 2022
Abstract
We study the symplectic geometry of derived intersections of Lagrangian morphisms. In particular, we show that for a functional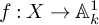 
$f : X \rightarrow \mathbb {A}_{k}^{1}$, the derived critical locus has a natural Lagrangian fibration 
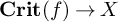$\textbf {Crit}(f) \rightarrow X$. In the case where f is nondegenerate and the strict critical locus is smooth, we show that the Lagrangian fibration on the derived critical locus is determined by the Hessian quadratic form.
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 23 , Issue 1 , January 2024 , pp. 311 - 345
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
Behrend, K. and Fantechi, B.,Symmetric obstruction theories and Hilbert schemes of points on threefolds, Algebra NumberTheory 2(3) (2008), 313–345.CrossRefGoogle Scholar
Brav, C., Bussi, V. and
Joyce, D., A Darboux theorem for derived schemes withshifted symplectic structure, J. Amer. Math. Soc. 32(2) (2019),399–443.CrossRefGoogle Scholar
Calaque, D., Three lectures on derived symplectic geometry andtopological field theories, Indag. Math. (N.S.) 25(5) (2014),926–947.CrossRefGoogle Scholar
Calaque, D., Lagrangian structures on mapping stacks andsemi-classical TFTs, in Stacks and Categories in Geometry, Topology, and Algebra volume 643of Contemp. Math., pp. 1–23. (Amer. Math. Soc.,Providence, RI, 2015).Google Scholar
Calaque, D., Shifted cotangent stacks are shiftedsymplectic, Ann. Fac. Sci. Toulouse Math. (6) 28(1) (2019),67–90.CrossRefGoogle Scholar
Calaque, D. Derived Stacks in Symplectic Geometry volume2, pp. 155–201 (Cambridge University Press,2021).Google Scholar
Calaque, D., Pantev, T.,Toën, B.,Vaquié, M. and
Vezzosi, G., Shifted Poisson structures anddeformation quantization, J. Topol. 10(2) (2017),483–584.CrossRefGoogle Scholar
Hablicsek, M., Derived intersections over the Hochschild cochain complex. arXiv e-prints,August 2016, page arXiv:1608.06965.Google Scholar
Joyce, D., A classical model for derived criticalloci, J. Differential Geom. 101(2) (2015) ,289–367.CrossRefGoogle Scholar
Lurie, J., Derived algebraic geometry. Massachusetts Institute of Technology, 2004. Thesis (Ph.D.)–Massachusetts Institute ofTechnology.Google Scholar
Lurie, J., Derived Algebraic Geometry V: Structured Spaces. arXive-prints, May 2009, page arXiv:0905.0459.Google Scholar
Pantev, T., Toën, B.,Vaquié, M. and
Vezzosi, G., Shifted symplecticstructures, Publ. Math. Inst. Hautes Études Sci. 117 (2013),271–328.CrossRefGoogle Scholar
Safronov, P., Quasi-Hamiltonian reduction via classicalChern–Simons theory, Advances in Mathematics 287 (2016),733–773.CrossRefGoogle Scholar
Schürg, T., Toën, B. and Vezzosi, G., Derived algebraic geometry,determinants of perfect complexes, and applications to obstruction theories for maps and complexes, J. Reine Angew.Math. 702 (2015), 1–40.CrossRefGoogle Scholar
Toën, B. Derived algebraic geometry,EMS Surv. Math. Sci., 1(2) (2014),153–240.CrossRefGoogle Scholar
Toën, B. and Vezzosi, G., Homotopical algebraic geometry, I. Topos theory, Adv. Math. 193(2) (2005), 257–372.Google Scholar
Toën, B. and Vezzosi, G., Homotopical algebraic geometry. II. Geometric stacks andapplications, Mem. Amer. Math. Soc. 193(902) (2008),x+224.Google Scholar
Vezzosi, G., Basic structures on derived criticalloci, Differential Geometry and its Applications 71 (2020),101635.CrossRefGoogle Scholar
Xu, P. Momentum maps and Morita equivalence,J. Differential Geom. 67(2) (2004), 289–333,06.CrossRefGoogle Scholar