Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-07T00:22:24.100Z Has data issue: false hasContentIssue false
  • English
  • Français

De Branges’ theorem on approximation problems of Bernstein type

Part of: Approximations and expansions Linear function spaces and their duals Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  27 February 2013

Anton Baranov  and
Harald Woracek
Anton Baranov
Affiliation:
Department of Mathematics and Mechanics, Saint Petersburg State University, 28, Universitetski pr., 198504 Petrodvorets, Russia (a.baranov@ev13934.spb.edu)
Harald Woracek
Affiliation:
Institut für Analysis und Scientific Computing, Technische Universität Wien, Wiedner Hauptstraße. 8–10/101, 1040 Wien, Austria (harald.woracek@tuwien.ac.at)
Get access Rights & Permissions [Opens in a new window]

Abstract

The Bernstein approximation problem is to determine whether or not the space of all polynomials is dense in a given weighted 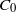${C}_{0} $-space on the real line. A theorem of de Branges characterizes non-density by existence of an entire function of Krein class being related with the weight in a certain way. An analogous result holds true for weighted sup-norm approximation by entire functions of exponential type at most $\tau $ and bounded on the real axis (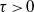$\tau \gt 0$ fixed).

We consider approximation in weighted 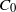${C}_{0} $-spaces by functions belonging to a prescribed subspace of entire functions which is solely assumed to be invariant under division of zeros and passing from 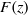$F(z)$ to 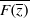$ \overline{F( \overline{z} )} $, and establish the precise analogue of de Branges’ theorem. For the proof we follow the lines of de Branges’ original proof, and employ some results of Pitt.

Keywords

weighted sup-norm approximationBernstein type problemde Branges’ theorem

MSC classification

Secondary: 41A30: Approximation by other special function classes 30D15: Special classes of entire functions and growth estimates 46E15: Banach spaces of continuous, differentiable or analytic functions 46E22: Hilbert spaces with reproducing kernels (=
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 4 , October 2013 , pp. 879 - 899
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhiezer, N. I., On weighted approximations of continuous functions by polynomials on the entire number axis. (Russian), Uspekhi Mat. Nauk (N.S.) 11 (4(70)) (1956), 3–43.Google Scholar
Akhiezer, N. I., The classical moment problem and some related topics in analysis (transl. from Russian) Gosudarstv. Izdat. Fiz.-Mat. Lit., Moscow 1961. English translation: Oliver & Boyd Edinburgh 1965.Google Scholar
Bakan, A. G., Representation of measures with polynomial denseness in ${L}^{p} ( \mathbb{R} , \mu )$, $0\lt p\lt \infty $, and its applications to determinate moment problems, Proc. Amer. Math. Soc. 136 (10) (2008), 3579–3589.Google Scholar
Borichev, A. and Sodin, M., Weighted exponential approximation and non-classical orthogonal spectral measures, Adv. Math. 226 (3) (2011), 2503–2545.Google Scholar
de Branges, L., The Stone–Weierstrass theorem, Proc. Amer. Math. Soc. 10 (1959), 822–824.Google Scholar
de Branges, L., The Bernstein problem, Proc. Amer. Math. Soc. 10 (1959), 825–832.Google Scholar
Koosis, P., The logarithmic integral. I.Cambridge Studies in Advanced Mathematics, Volume 12 (Cambridge University Press, Cambridge, 1988).Google Scholar
Lubinsky, D. S., A survey of weighted polynomial approximation with exponential weights, Surv. Approx. Theory 3 (2007), 1–105.Google Scholar
Mergelyan, S. N., Weighted approximations by polynomials (transl. from Russian), Uspekhi Mat. Nauk (N.S.) 11 (5(71)) (1956), 107–152 English translation: 1958 American Mathematical Society Translations, Ser. 2, Volume 10 pp. 59–106.Google Scholar
Nachbin, L., Weighted approximation for algebras and modules of continuous functions: Real and self-adjoint complex cases, Ann. of Math. (2) 81 (1965), 289–302.Google Scholar
Pitt, L. D., A general approach to approximation problems of the Bernstein type, Adv. Math. 49 (3) (1983), 264–299.Google Scholar
Pollard, H., Solution of Bernstein’s approximation problem, Proc. Amer. Math. Soc. 4 (1953), 869–875.Google Scholar
Poltoratski, A., Bernstein’s problem on weighted polynomial approximation (arXiv:1110.2540v2) 28 Oct. 2011.Google Scholar
Rudin, W., Real and complex analysis, Third edition. (McGraw-Hill Book Co, New York, 1987).Google Scholar
Sodin, M. and Yuditskii, P., Another approach to de Branges’ theorem on weighted polynomial approximation, Proceedings of the Ashkelon Workshop on Complex Function Theory (1996), 221–227, Israel Math. Conf. Proc., 11, Bar-Ilan Univ., Ramat Gan, 1997.Google Scholar
Summers, W. H., A representation theorem for biequicontinuous completed tensor products of weighted spaces, Trans. Amer. Math. Soc. 146 (1969), 121–131.Google Scholar
Summers, W. H., Dual spaces of weighted spaces, Trans. Amer. Math. Soc. 151 (1970), 323–333.Google Scholar