Article contents
Structural results for free Araki–Woods factors and their continuous cores
Published online by Cambridge University Press: 18 February 2010
Abstract
We show that for any type III1 free Araki–Woods factor 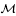 = (HR, Ut)″ associated with an orthogonal representation (Ut) of R on a separable real Hilbert space HR, the continuous core M =
= (HR, Ut)″ associated with an orthogonal representation (Ut) of R on a separable real Hilbert space HR, the continuous core M = 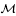 ⋊σR is a semisolid II∞ factor, i.e. for any non-zero finite projection q ∈ M, the II1 factor qM q is semisolid. If the representation (Ut) is moreover assumed to be mixing, then we prove that the core M is solid. As an application, we construct an example of a non-amenable solid II1 factor N with full fundamental group, i.e.
⋊σR is a semisolid II∞ factor, i.e. for any non-zero finite projection q ∈ M, the II1 factor qM q is semisolid. If the representation (Ut) is moreover assumed to be mixing, then we prove that the core M is solid. As an application, we construct an example of a non-amenable solid II1 factor N with full fundamental group, i.e. 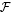 (N) = R*+, which is not isomorphic to any interpolated free group factor L(Ft), for 1 < t ≤ = +∞.
(N) = R*+, which is not isomorphic to any interpolated free group factor L(Ft), for 1 < t ≤ = +∞.
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 9 , Issue 4 , October 2010 , pp. 741 - 767
- Copyright
- Copyright © Cambridge University Press 2010
References
- 6
- Cited by




