Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-25T01:07:59.170Z Has data issue: false hasContentIssue false
  • English
  • Français

PERVERSE MOTIVES AND GRADED DERIVED CATEGORY 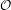${\mathcal{O}}$

Part of: Cycles and subschemes Special varieties Lie algebras and Lie superalgebras Lie groups

Published online by Cambridge University Press:  26 February 2016

Wolfgang Soergel  and
Matthias Wendt
Wolfgang Soergel
Affiliation:
Mathematisches Institut, Albert-Ludwigs-Universität Freiburg, Eckerstraße 1, 79104 Freiburg im Breisgau, Germany (wolfgang.soergel@math.uni-freiburg.de)
Matthias Wendt
Affiliation:
Fakultät für Mathematik, Universität Duisburg-Essen, Thea-Leymann-Strasse 9, 45127 Essen, Germany (matthias.wendt@uni-due.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

For a variety with a Whitney stratification by affine spaces, we study categories of motivic sheaves which are constant mixed Tate along the strata. We are particularly interested in those cases where the category of mixed Tate motives over a point is equivalent to the category of finite-dimensional bigraded vector spaces. Examples of such situations include rational motives on varieties over finite fields and modules over the spectrum representing the semisimplification of de Rham cohomology for varieties over the complex numbers. We show that our categories of stratified mixed Tate motives have a natural weight structure. Under an additional assumption of pointwise purity for objects of the heart, tilting gives an equivalence between stratified mixed Tate sheaves and the bounded homotopy category of the heart of the weight structure. Specializing to the case of flag varieties, we find natural geometric interpretations of graded category 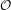${\mathcal{O}}$ and Koszul duality.

Keywords

mixed Tate motivesperverse sheavesmixed geometrycategory 𝓞

MSC classification

Primary: 14C15: (Equivariant) Chow groups and rings; motives 14M15: Grassmannians, Schubert varieties, flag manifolds 17B10: Representations, algebraic theory (weights) 22E47: Representations of Lie and real algebraic groups
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 2 , April 2018 , pp. 347 - 395
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achar, P. N. and Kitchen, S., Koszul duality and mixed Hodge modules, Int. Math. Res. Not. IMRN (2014), 5874–5911.Google Scholar
Achar, P. N. and Riche, S., Koszul duality and semisimplicity of Frobenius, Ann. Inst. Fourier (Grenoble) 63 (2013), 1511–1612.Google Scholar
Achar, P. N. and Riche, S., Modular perverse sheaves on flag varieties I: tilting and parity sheaves, avec un appendice en collaboration avec G. Williamson, to appear in Ann. Sci. Éc. Norm. Supér (arXiv:1401.7245. hal:00937989).Google Scholar
Achar, P. N. and Riche, S., Modular perverse sheaves on flag varieties II: Koszul duality and formality, Duke Math. J. 165(1) (2016), 161–215.Google Scholar
Ayoub, J., Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique I, Astérisque 314 (2007).Google Scholar
Ayoub, J., Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique II, Astérisque 315 (2007).Google Scholar
Ayoub, J., A guide to (étale) motivic sheaves, Proceedings of the ICM, 2014.Google Scholar
Beilinson, A. A., Bernstein, J. N. and Deligne, P., Faisceaux pervers, Astérisque 100 (1982), 1–172.Google Scholar
Beilinson, A. A. and Ginsburg, V., Mixed categories, Ext-duality and representations (results and conjectures), Preprint, 1986.Google Scholar
Beilinson, A. A., Ginzburg, V. and Soergel, W., Koszul duality patterns in representation theory, J. Amer. Math. Soc. 9(2) (1996), 473–527.Google Scholar
Bezrukavnikov, R. and Yun, Z., On Koszul duality for Kac-Moody groups, Represent. Theory 17 (2013), 1–98.Google Scholar
Bondarko, M. V., Weight structures versus t-structures; weight filtrations, spectral sequences, and complexes (for motives and in general), J. K-Theory 6(3) (2010), 387–504, MR 2746283.CrossRefGoogle Scholar
Bondarko, M. V., Weights for relative motives: relation with mixed complexes of sheaves, Int. Math. Res. Not. IMRN 17 (2014), 4715–4767.Google Scholar
Borel, A., Linear algebraic groups, in Graduate Texts in Mathematics, 2nd enlarged edn, Volume 126 (Springer, 1991).Google Scholar
Cisinski, D.-C. and Déglise, F., Mixed Weil cohomologies, Adv. Math. 230 (2012), 55–130.CrossRefGoogle Scholar
Cisinski, D.-C. and Déglise, F., Triangulated categories of mixed motives, 2012, arXiv:0912.2110v3.Google Scholar
Deligne, P., Structures de Hodge mixtes réelles, in Motives. Proc. Sympos. Pure Math., Volume 55, pp. 509–514 (AMS, 1994).Google Scholar
Drew, B., Réalizations tannakiennes des motifs mixtes triangulés, PhD thesis, Paris 13, 2013.Google Scholar
Friedlander, E. M., Suslin, A. and Voevodsky, V., Cycles, transfers, and motivic homology theories, in Annals of Mathematics Studies, Volume 143 (Princeton University Press, 2000).Google Scholar
Ginzburg, V., Perverse sheaves and ℂ∗ -actions, J. Amer. Math. Soc. 4(3) (1991), 483–490.Google Scholar
Haines, T. J., A proof of the Kazhdan–Lusztig purity theorem via the decomposition theorem of BBD, Note.Google Scholar
Harder, G., Die Kohomologie S-arithmetischer Gruppen über Funktionenkörpern, Invent. Math. 42 (1977), 135–175, MR 0473102 (57 #12780).Google Scholar
Hébert, D., Structure de poids à la Bondarko sur les motifs de Beilinson, Compos. Math. 147(5) (2011), 1447–1462, MR 2834728 (2012i:14026).Google Scholar
Hovey, M., Spectra and symmetric spectra in general model categories, J. Pure Appl. Algebra 165 (2001), 63–127.Google Scholar
Keller, B., Deriving dg-categories, Ann. Ec. Sup. 27 (1994), 63–102.Google Scholar
Levine, M., Tate motives and the vanishing conjectures for algebraic K-theory, in Algebraic K-Theory and Algebraic Topology, (ed. Goerss, P. G. and Jardine, J. F.), NATO ASI Series, Series C, Volume 407, pp. 167–188 (Kluwer Acad. Publ., Dordrecht, 1993).Google Scholar
Levine, M., Tate motives and the fundamental group, in Cycles, Motives and Shimura Varieties, Tata Inst. Fund. Res. Stud. Math., pp. 265–392 (Kluwer, 2010).Google Scholar
Quillen, D., On the cohomology and K-theory of the general linear groups over a finite field, Ann. of Math. (2) 96 (1972), 552–586, MR 0315016 (47 #3565).CrossRefGoogle Scholar
Rickard, J., Morita theory for derived categories, J. Lond. Math. Soc. (2) 39(3) (1989), 436–456.Google Scholar
Soergel, W., n-cohomology of simple highest weight modules on walls and purity, Invent. Math. 98 (1989), 565–580.Google Scholar
Soergel, W., Kategorie 𝓞, perverse Garben und Moduln über den Koinvarianten zur Weylgruppe, J. Amer. Math. Soc. 3 (1990), 421–445.Google Scholar
Spaltenstein, N., Resolutions of unbounded complexes, Compos. Math. 65(2) (1988), 121–154.Google Scholar
Springer, T. A., A purity result for fixed point varieties in flag manifolds, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 31(2) (1984), 271–282.Google Scholar
Virk, R., Some geometric facets of the Langlands correspondence for real groups, Bull. Lond. Math. Soc. 47(2) (2015), 225–232.Google Scholar
Wildeshaus, J., Notes on Artin-Tate motives, Preprint, arXiv:0811.4551v2.Google Scholar
Wildeshaus, J., f-catégories, tours et motifs de Tate, C. R. Math. Acad. Sci. Paris 347(23–24) (2009), 1337–1342, MR 2588777 (2010j:18023).Google Scholar
Wildeshaus, J., Intermediate extension of Chow motives of Abelian type, 2012, arXiv:1211.5327v2.Google Scholar