Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-23T19:27:55.407Z Has data issue: false hasContentIssue false
  • English
  • Français

MOTIVIC HILBERT ZETA FUNCTIONS OF CURVES ARE RATIONAL

Part of: Arithmetic problems. Diophantine geometry Cycles and subschemes Curves

Published online by Cambridge University Press:  31 October 2018

Dori Bejleri ,
Dhruv Ranganathan  and
Ravi Vakil
Dori Bejleri
Affiliation:
Department of Mathematics, Brown University, Providence RI 02913, USA (dbejleri@math.brown.edu)
Dhruv Ranganathan
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02138, USA (dhruvr@mit.edu)
Ravi Vakil
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, USA (vakil@math.stanford.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

The motivic Hilbert zeta function of a variety 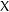$X$ is the generating function for classes in the Grothendieck ring of varieties of Hilbert schemes of points on 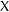$X$. In this paper, the motivic Hilbert zeta function of a reduced curve is shown to be rational.

Keywords

Hilbert schemeszeta functionscurve singularities

MSC classification

Primary: 14C05: Parametrization (Chow and Hilbert schemes) 14H20: Singularities, local rings 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 3 , May 2020 , pp. 947 - 964
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aganagic, M. and Shakirov, S., Knot homology from refined Chern–Simons theory, preprint, 2011, arXiv:1105.5117.Google Scholar
Bejleri, D., The Hilbert zeta function is constructible in families of curves, http://www.math.brown.edu/dbejleri/constructible.pdf (in preparation).Google Scholar
Buchweitz, R.-O. and Greuel, G.-M., The Milnor number and deformations of complex curve singularities, Invent. Math. 58 (1980), 241–281.Google Scholar
de Cataldo, M. A. A. and Migliorini, L., The Chow groups and the motive of the Hilbert scheme of points on a surface, J. Algebra 251 (2002), 824–848.Google Scholar
Eisenbud, D., Commutative Algebra: with a View Toward Algebraic Geometry, vol. 150 (Springer Science & Business Media, New York, 2013).Google Scholar
Fantechi, B., Göttsche, L., Illusie, L., Kleiman, S. L., Nitsure, N. and Vistoli, A., Fundamental Algebraic Geometry, Mathematical Surveys and Monographs, Volume 123, (American Mathematical Society, Providence, RI, 2005). Grothendieck’s FGA explained.Google Scholar
Goldin, R. and Teissier, B., Resolving singularities of plane analytic branches with one toric morphism, in Resolution of Singularities (Obergurgl, 1997), Progress in Mathematics, Volume 181, pp. 315–340 (Birkhäuser, Basel, 2000).Google Scholar
Göttsche, L., The Betti numbers of the Hilbert scheme of points on a smooth projective surface, Math. Ann. 286 (1990), 193–207.Google Scholar
Göttsche, L., On the motive of the Hilbert scheme of points on a surface, Math. Res. Lett. 8 (2001), 613–627.Google Scholar
Gyenge, Á., Némethi, A. and Szendrői, B., Euler characteristics of Hilbert schemes of points on simple surface singularities, Eur. J. Math. 4 (2018), 439. doi:10.1007/s40879-018-0222-4.Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, Volume 52, (Springer, New York, Heidelberg, 1977).Google Scholar
Kapranov, M., The elliptic curve in the S-duality theory and Eisenstein series for Kac–Moody groups, ArXiv Mathematics e-prints (2000).Google Scholar
Kaveh, K. and Murata, T., Toric degenerations of projective varieties, ArXiv e-prints (2017).Google Scholar
Litt, D., Zeta functions of curves with no rational points, Michigan Math. J. 64 (2015), 383–395.Google Scholar
Maulik, D. and Yun, Z., Macdonald formula for curves with planar singularities, J. Reine Angew. Math. 2014 (2014), 27–48.Google Scholar
Migliorini, L. and Shende, V., A support theorem for Hilbert schemes of planar curves, J. Eur. Math. Soc. (JEMS) 15 (2013), 2353–2367.Google Scholar
Oblomkov, A. and Shende, V. et al. , The Hilbert scheme of a plane curve singularity and the HOMFLY polynomial of its link, Duke Math. J. 161 (2012), 1277–1303.Google Scholar
Pfister, G. and Steenbrink, J. H. M., Reduced Hilbert schemes for irreducible curve singularities, J. Pure Appl. Algebra 77 (1992), 103–116.Google Scholar
Schwede, K., Obtaining non-normal varieties by pushout. MathOverflow. https://mathoverflow.net/q/186650 (version: 2014-11-09).Google Scholar
Teissier, B., Résolution simultanée : I - familles de courbes, Séminaire sur les singularités des surfaces (1976–1977), pp. 1–10.Google Scholar
The Stacks Project Authors, Stacks project. http://stacks.math.columbia.edu(2017).Google Scholar
Zheng, X., The Hilbert schemes of points on singular varieties and Kodaira non-vanishing in characteristic p, PhD thesis (2016).Google Scholar