Article contents
Bruhat–Tits theory from Berkovich's point of view. II Satake compactifications of buildings
Published online by Cambridge University Press: 13 December 2011
Abstract
In the paper ‘Bruhat–Tits theory from Berkovich's point of view. I. Realizations and compactifications of buildings’, we investigated various realizations of the Bruhat–Tits building 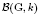 of a connected and reductive linear algebraic group G over a non-Archimedean field k in the framework of Berkovich's non-Archimedean analytic geometry. We studied in detail the compactifications of the building which naturally arise from this point of view. In the present paper, we give a representation theoretic flavour to these compactifications, following Satake's original constructions for Riemannian symmetric spaces.
of a connected and reductive linear algebraic group G over a non-Archimedean field k in the framework of Berkovich's non-Archimedean analytic geometry. We studied in detail the compactifications of the building which naturally arise from this point of view. In the present paper, we give a representation theoretic flavour to these compactifications, following Satake's original constructions for Riemannian symmetric spaces.
We first prove that Berkovich compactifications of a building coincide with the compactifications, previously introduced by the third named author and obtained by a gluing procedure. Then we show how to recover them from an absolutely irreducible linear representation of G by embedding 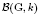 in the building of the general linear group of the representation space, compactified in a suitable way. Existence of such an embedding is a special case of Landvogt's general results on functoriality of buildings, but we also give another natural construction of an equivariant embedding, which relies decisively on Berkovich geometry.
in the building of the general linear group of the representation space, compactified in a suitable way. Existence of such an embedding is a special case of Landvogt's general results on functoriality of buildings, but we also give another natural construction of an equivariant embedding, which relies decisively on Berkovich geometry.
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 11 , Issue 2 , April 2012 , pp. 421 - 465
- Copyright
- Copyright © Cambridge University Press 2012
References
- 5
- Cited by




