Article contents
Algebraic cycles on the relative symmetric powers and on the relative Jacobian of a family of curves. II
Published online by Cambridge University Press: 23 March 2010
Abstract
Let C be a family of curves over a non-singular variety S. We study algebraic cycles on the relative symmetric powers C[n] and on the relative Jacobian J. We consider the Chow homology CH*(C[∙]/S) := ⊕n CH*(C[n]/S) as a ring using the Pontryagin product. We prove that CH*(C[∙]/S) is isomorphic to CH*(J/S)[t]〈u〉, the PD-polynomial algebra (variable: u) over the usual polynomial ring (variable: t) over CH*(J/S). We give two such isomorphisms that over a general base are different. Further we give precise results on how CH*(J/S) sits embedded in CH*(C[∙]/S) and we give an explicit geometric description of how the operators 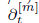 and ∂u act. This builds upon the study of certain geometrically defined operators Pi,j (a) that was undertaken by one of us.
and ∂u act. This builds upon the study of certain geometrically defined operators Pi,j (a) that was undertaken by one of us.
Our results give rise to a new grading on CH*(J/S). The associated descending filtration is stable under all operators [N]*, and [N]* acts on 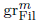 as multiplication by Nm. Hence, after − ⊗ ℚ this filtration coincides with the one coming from Beauville's decomposition. The grading we obtain is in general different from Beauville's.
as multiplication by Nm. Hence, after − ⊗ ℚ this filtration coincides with the one coming from Beauville's decomposition. The grading we obtain is in general different from Beauville's.
Finally, we give a version of our main result for tautological classes, and we show how our methods give a simple geometric proof of some relations obtained by Herbaut and van der Geer–Kouvidakis, as later refined by one of us.
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 9 , Issue 4 , October 2010 , pp. 799 - 846
- Copyright
- Copyright © Cambridge University Press 2010
References
- 3
- Cited by




