Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-25T21:27:24.666Z Has data issue: false hasContentIssue false
  • English
  • Français

REFLECTORS AND GLOBALIZATIONS OF PARTIAL ACTIONS OF GROUPS

Part of: Rings and algebras with additional structure Other classes of algebra General theory of categories and functors Algebraic structures Varieties

Published online by Cambridge University Press:  14 August 2017

MYKOLA KHRYPCHENKO Open the ORCID record for MYKOLA KHRYPCHENKO [Opens in a new window]  and
BORIS NOVIKOV
MYKOLA KHRYPCHENKO*
Affiliation:
Departamento de Matemática, Universidade Federal de Santa Catarina, Campus Reitor João David Ferreira Lima, Florianópolis, SC, CEP: 88040–900, Brazil email nskhripchenko@gmail.com
BORIS NOVIKOV
Affiliation:
Department of Mechanics and Mathematics, V. N. Karazin Kharkiv National University, Svobody sq. 4, Kharkiv, 61077, Ukraine email boris.v.novikov@univer.kharkov.ua
*
✉nskhripchenko@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a partial action 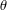$\unicode[STIX]{x1D703}$ of a group on a set with an algebraic structure, we construct a reflector of 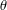$\unicode[STIX]{x1D703}$ in the corresponding subcategory of global actions and study the question when this reflector is a globalization. In particular, if $\unicode[STIX]{x1D703}$ is a partial action on an algebra from a variety 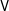$\mathsf{V}$, then we show that the problem reduces to the embeddability of a certain generalized amalgam of 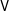$\mathsf{V}$-algebras associated with 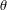$\unicode[STIX]{x1D703}$. As an application, we describe globalizable partial actions on semigroups, whose domains are ideals.

Keywords

partial actionreflectorglobalization

MSC classification

Primary: 18A40: Adjoint functors (universal constructions, reflective subcategories, Kan extensions, etc.) 08C05: Categories of algebras
Secondary: 08A02: Relational systems, laws of composition 08A55: Partial algebras 08B25: Products, amalgamated products, and other kinds of limits and colimits 16W22: Actions of groups and semigroups; invariant theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 104 , Issue 3 , June 2018 , pp. 358 - 379
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

First author is partially supported by FAPESP of Brazil (process: 2012/01554–7).

Second author was deceased on 30 March 2014.

References

Abadie, F., ‘Enveloping actions and Takai duality for partial actions’, J. Funct. Anal. 197(1) (2003), 14–67.Google Scholar
Adámek, J. and Trnková, V., Automata and Algebras in Categories, Mathematics and its Applications, 37 (Kluwer Academic Publishers, Dordrecht, 1990).Google Scholar
Clifford, A. and Preston, G., The Algebraic Theory of Semigroups, Mathematical Surveys and Monographs 7, 1 (American Mathematical Society, Providence, RI, 1961).Google Scholar
Cohn, P. M., Universal Algebra, 2nd edn, Vol. 6 (Reidel Publishing Co., Dordrecht–Boston, MA, 1981).CrossRefGoogle Scholar
Dokuchaev, M., del Río, Á. and Simón, J. J., ‘Globalizations of partial actions on nonunital rings’, Proc. Amer. Math. Soc. 135(2) (2007), 343–352.Google Scholar
Dokuchaev, M. and Exel, R., ‘Associativity of crossed products by partial actions, enveloping actions and partial representations’, Trans. Amer. Math. Soc. 357(5) (2005), 1931–1952.CrossRefGoogle Scholar
Dokuchaev, M. and Novikov, B., ‘Partial projective representations and partial actions’, J. Pure Appl. Algebra 214(3) (2010), 251–268.Google Scholar
Exel, R., ‘Partial actions of groups and actions of inverse semigroups’, Proc. Amer. Math. Soc. 126(12) (1998), 3481–3494.Google Scholar
Ferrero, M., ‘Partial actions of groups on semiprime rings’, in: Groups, Rings and Group Rings, Lecture Notes in Pure and Applied Mathematics, 248 (Chapman & Hall/CRC, Boca Raton, FL, 2006), 155–162.Google Scholar
Grätzer, G., Universal Algebra, 2nd edn (Springer, New York, 2008).Google Scholar
Grillet, P. A. and Petrich, M., ‘Free products of semigroups amalgamating an ideal’, J. Lond. Math. Soc. (2) 2 (1970), 389–392.Google Scholar
Kellendonk, J. and Lawson, M. V., ‘Partial actions of groups’, Internat. J. Algebra Comput. 14(1) (2004), 87–114.Google Scholar
Ljapin, E. S. and Evseev, A. E., The Theory of Partial Algebraic Operations, Mathematics and its Applications, 414 (Springer Science+Business Media, B.V., Dordrecht, 1997).Google Scholar
Mac Lane, S., Categories for the Working Mathematician (Springer, New York–Heidelberg–Berlin, 1971).Google Scholar
Mal’cev, A. I., Algebraic Systems (Springer, Berlin–Heidelberg–New York, 1973).CrossRefGoogle Scholar
Neumann, H., ‘Generalized free products with amalgamated subgroups I’, Amer. J. Math. 70 (1948), 590–625.Google Scholar
Neumann, H., ‘Generalized free products with amalgamated subgroups II’, Amer. J. Math. 71 (1949), 491–540.Google Scholar
Neumann, H., ‘Generalized free sums of cyclical groups’, Amer. J. Math. 72 (1950), 671–685.CrossRefGoogle Scholar
Neumann, H., ‘On an amalgam of Abelian groups’, J. Lond. Math. Soc. (2) 26 (1951), 228–232.CrossRefGoogle Scholar
Neumann, B. H., ‘An essay on free products of groups with amalgamations’, Philos. Trans. R. Soc. Lond. Ser. A 246 (1954), 503–554.Google Scholar
Neumann, B. H. and Neumann, H., ‘A contribution to the embedding theory of group amalgams’, Proc. Lond. Math. Soc. (3) 3 (1953), 243–256.Google Scholar
Terese, Term Rewriting Systems, Cambridge Tracts in Theoretical Computer Science, 55(Cambridge University Press, Cambridge, 2003).Google Scholar
Tsalenko, M. Sh. and Shul’geĭfer, E. G., ‘Foundations of category theory’, Modern Algebra (Nauka, Moscow, 1974), (Russian).Google Scholar