Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-20T15:19:51.720Z Has data issue: false hasContentIssue false
  • English
  • Français

On typical means of fourier series of continuous functions

Published online by Cambridge University Press:  09 April 2009

B. Kwee
B. Kwee
Affiliation:
Department of Mathematics University of MalayaKuala LumpurMalaysia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f(x) be continuous in (-π, π) and periodic with period 2π and let 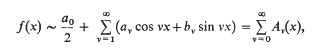, 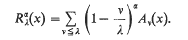The aim of this paper is to prove the following theorem.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 13 , Issue 1 , February 1972 , pp. 71 - 75
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Hobson, E. W., Functions of a real variable, Vol. II (Cambridge, 1926).Google Scholar
[2]Kwee, B., ‘The approximation of continuous functions by Riesz typical means of their Fourier series’, Jour. Australian Math. Soc. 7 (1967), 539–544.Google Scholar
[3]Kwee, B., ‘'A note in the approximation of continuous functions by Riesz typical means of their Fourier series’, Jour. Australian Math. Soc. 9 (1969), 180–181.CrossRefGoogle Scholar