Hostname: page-component-7bb8b95d7b-lvwk9 Total loading time: 0 Render date: 2024-09-17T07:39:44.350Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on approximation by automorphic images of functions in L1 and L∞

Published online by Cambridge University Press:  09 April 2009

S. R. Harasymiv
S. R. Harasymiv
Affiliation:
Department of MathematicsInstitute of Advanced Studies Australian National University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [1], it was shown that if ƒ ∈ Lp(Rn), where 1 < p < ∞, then the closed subspace of Lp (Rn) spanned by functions of the form 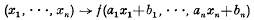[where a1, …, an, b1, …, bn, are real numbers; ak, ≠ 0; k = 1, …, n] coincides with the whole of Lp(Rn). In the present note, analogous results are derived for the spaces of integrable functions, essentially bounded measurable functions, bounded continuous functions, and continuous functions vanishing at infinity.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 2 , May 1968 , pp. 222 - 230
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Harasymiv, S. R., ‘A note on dilations in Lp’. Pacific J. Math. 21(1967), 493–501.CrossRefGoogle Scholar
[2]Herz, C. S., ‘Spectral theory of bounded functions,’ Trans. Amer. Math. 94 (1960), 181–232.CrossRefGoogle Scholar
[3]Edwards, R. E., ‘Supports and singular supports of pseudomeasures,’ J. Aust. Math. Soc. 6 (1966), 65–75.CrossRefGoogle Scholar
[4]Edwards, R. E., ‘Spans of translates in Lp(G)’. J. Aust. Math. Soc. 5 (1965), 216–233.CrossRefGoogle Scholar
[5]Gaudry, G. I., ‘Quasimeasures and operators commuting with convolution’. Pacific J. Math. 18 (1966), 461–476.CrossRefGoogle Scholar
[6]Gaudry, G. I., ‘Multipliers of type (p,q)’. Pacific J. Math. 18 (1966), 477–488.CrossRefGoogle Scholar
[7]Rudin, W., Fourier Analysis on Groups (Interscience Publishers, N.Y., 1962).Google Scholar
[8]Schwartz, Laurent., Théorie des Distributions (Hermann, Paris).Google Scholar
[9]Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis (Springer-Verlag, 1963).Google Scholar