Hostname: page-component-77c89778f8-gq7q9 Total loading time: 0 Render date: 2024-07-24T06:36:20.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite τT products of distribution functions

Part of: Probability theory on algebraic and topological structures Limit theorems

Published online by Cambridge University Press:  09 April 2009

Richard Moynihan
Richard Moynihan
Affiliation:
Analysis Department The MITRE Corporation, Bedford, Massachusetts 01730, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T be a continuous t-norm (a suitable binary operation on[0, 1]) and Δ + the space of distribution functions which are concertratede on [0,∞. theτT product of any F, G in Δ+ is defined at any real x by 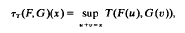, and the pair (Δ+, τT) forms a semigroup. Thus, given a sequence {Fi} in Δ+, the n-fold product τT(F1 … Fn) is well-defined for each n. Moreover, that resulting sequence {τT(F1, …, Fn)} is pointwise non-increasing and hence has a weak limit. This paper establishes a convergence theorem which yields a representation for this weak limit. In addition, we prove the Zero-One law that, for Archimedean t-norms, the weak limit is either identically zero or has supremum 1.

MSC classification

Secondary: 60F99: None of the above, but in this section 60B99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 26 , Issue 2 , September 1978 , pp. 227 - 240
Copyright
Copyright © Australian Mathematical Society 1978

References

Aczél, J. (1966), Lectures on functional equations and their applications, (Academic Press, New York).Google Scholar
Ling, C. H. (1965), ‘Representation of associative functions’, Publ. Math., Debrecen, 12, 189–212.Google Scholar
Moynihan, R. (1977), ‘Conjugate transforms for τT semigroups of probability distribution functions’, J. Math. Anal. and Appl., to appear.Google Scholar
Moynihan, R. (to appear), ‘Conjugate transforms and limit theorems for TT semigroups’.Google Scholar
Miranda, A. B. Paalman-de (1964), Topological semigroups, Mathematical Centre Tracts, No. 11 (Mathematisch Centrum Amsterdam).Google Scholar
Schweizer, B. (1967), ‘Probabilistic metric spaces—the first 25 years’, The New York Statistician, 19, 3–6.Google Scholar
Schweizer, B. (1975), ‘Multiplications on the space of probability distribution functions’, Aequationes Math., 12, 156–183.Google Scholar
Schweizer, B. and Sklar, A. (1974), ‘Operations on distribution functions not derivable from operations on random variables’, Studia Math., 52, 43–52.Google Scholar