Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-27T09:20:46.428Z Has data issue: false hasContentIssue false
  • English
  • Français

Factorization structures and subcategories of the category of topological spaces

Published online by Cambridge University Press:  09 April 2009

Ryosuke Nakagawa
Ryosuke Nakagawa
Affiliation:
Department of MathematicsTokyo University of Education Otsuka, Bunkyo-Ku, Tokyo.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Various investigations on (E, M)-categories are given by many authors. Recently, Herrlich (to appear) and Strecker (1972) gave interesting results on relations between factorizations (E, M) on nice categories 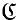and epireflective subcategories of 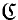. Factorization (E, M) treated by them satisfy that E ⊂ Epi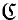. In this paper we shall consider factorization structures (E, M) such that E⊃Epi 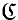in the category 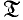of all topological spaces and study relations between these structures and some subcategories of 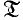. Our results are quite different from those in Herrlich (to appear) and Strecker (1972) and are rather related with the results in Herrlich (1969). Herrlich (1969) defined limit operators on 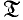and gave a one-to-one correspondence between suitable limit operators and bicoreflective subcategories of 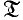. We shall consider two kinds of factorization structures on 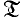and show that the first ones correspond to bicoreflective subcategories which are closed under closed embeddings, the second ones correspond to bireflective subcategories which satisfy that the classes of all reflections are closed under closed embeddings (see Proposition 11) and these correspondences are one-to-one.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 21 , Issue 2 , March 1976 , pp. 144 - 154
Copyright
Copyright © Australian Mathematical Society 1976

References

Herrlich, H. (1968), Topologische Reflexionen und Coreflexionen, Lecture Note 78 (springer, 1968).CrossRefGoogle Scholar
Herrlich, H. (1969), ‘Limit operators and topological coreflections’, Trans. Amer. Math. Soc. 146, 203–210.CrossRefGoogle Scholar
Herrlich, H. (1972), ‘Coreflective subcategories in general topology’, Fund. Math. 73, 199–218.CrossRefGoogle Scholar
H. Herrlich (to appear), ‘Perfect subcategories and factorizations’.Google Scholar
Kennison, J. F. (1968), ‘Full reflective subcategories and generalized covering spaces’, Illinois J. Math. 12, 353–365.Google Scholar
Mitchell, B. (1965), Theory of categories (Academic Press, New York, 1965).Google Scholar
Strecker, G. E. (1972), ‘Epireflection operator vs perfect morphisms and closed classes of epimorphisms’, Bull. Austral. Math. Soc. 7, 359–366.CrossRefGoogle Scholar