Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T05:57:42.163Z Has data issue: false hasContentIssue false
  • English
  • Français

CRITICAL BINOMIAL IDEALS OF NORTHCOTT TYPE

Part of: Theory of modules and ideals Rings and algebras with additional structure Arithmetic rings and other special rings

Published online by Cambridge University Press:  16 November 2020

P. A. GARCÍA‐SÁNCHEZ Open the ORCID record for P. A. GARCÍA‐SÁNCHEZ [Opens in a new window] ,
D. LLENA Open the ORCID record for D. LLENA [Opens in a new window]  and
I. OJEDA Open the ORCID record for I. OJEDA [Opens in a new window]
P. A. GARCÍA‐SÁNCHEZ
Affiliation:
Departamento de Álgebra, Universidad de Granada, E-18071Granada, España e-mail: pedro@ugr.es
D. LLENA*
Affiliation:
Departamento de Matemáticas, Universidad de Almeria, E-04120Almeria, España
I. OJEDA
Affiliation:
Departamento de Matemáticas, Universidad de Extremadura, E-06071Badajoz, España e-mail: ojedamc@unex.es
*
e-mail: dllena@ual.es
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study a family of binomial ideals defining monomial curves in the n-dimensional affine space determined by n hypersurfaces of the form 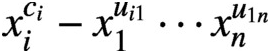$x_i^{c_i} - x_1^{u_{i1}} \cdots x_n^{u_{1n}}$ in $\Bbbk [x_1, \ldots , x_n]$ with 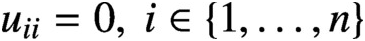$u_{ii} = 0, \ i\in \{ 1, \ldots , n\}$ . We prove that the monomial curves in that family are set-theoretic complete intersections. Moreover, if the monomial curve is irreducible, we compute some invariants such as genus, type and Frobenius number of the corresponding numerical semigroup. We also describe a method to produce set-theoretic complete intersection semigroup ideals of arbitrary large height.

Keywords

critical idealNorthcott idealgluing

MSC classification

Primary: 13F20: Polynomial rings and ideals; rings of integer-valued polynomials
Secondary: 13C40: Linkage, complete intersections and determinantal ideals 16W50: Graded rings and modules
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 1 , February 2021 , pp. 48 - 70
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by James East

The authors were supported by the project MTM2017-84890-P, which is funded by Ministerio de Economía y Competitividad and Fondo Europeo de Desarrollo Regional FEDER. The first and third authors were also partially supported by the project PGC2018-096446-B-C21 (MINECO/FEDER, UE). The first and second authors were supported by the Junta de Andalucía Grant Number FQM-343, and the third author was supported by the Junta de Extremadura Grant Number FQM024-GR18021 (FEDER, UE).

References

Alcántar, A. and Villarreal, R. H., ‘Critical binomials of monomial curves’, Comm. Algebra 22(8) (1994), 3037–3052.Google Scholar
Bigatti, A., La Scala, R. and Robbiano, L., ‘Computing toric ideals’, J. Symbolic Comput. 27 (1999), 351–365.Google Scholar
Bresinsky, H., ‘Binomial generating sets for monomial curves, with applications in ${\mathbb{A}}^{4}$ ’, Rend. Semin. Mat. Univ. Politec. Torino 46(3) (1988), 353–370.Google Scholar
Bullejos, M. and García-Sánchez, P. A., ‘Minimal presentations for monoids with the ascending chain condition on principal ideals’, Semigroup Forum 85 (2012), 185–1190.CrossRefGoogle Scholar
Chapman, S. T., García-Sánchez, P. A., Llena, D., Malyshev, A. and Steinberg, D., ‘On the Delta set and the Betti elements of a BF-monoid’, Arab J. Math. 1 (2012), 53–61.CrossRefGoogle Scholar
Chapman, S. T., García-Sánchez, P. A., Llena, D., Ponomarenko, V. and Rosales, J. C., ‘The catenary and tame degree in finitely generated commutative cancellative monoids’, Manuscripta Math. 120 (2006), 253–264.Google Scholar
Delgado, M., García-Sánchez, P. A. and Morais, J., ‘numericalsgps’: a gap package on numerical semigroups (http://www.gap-system.org/Packages/numericalsgps.html).Google Scholar
Eisenbud, D. and Sturmfels, B., ‘Binomial ideals’, Duke Math. J. 84(1) (1996),1–45.CrossRefGoogle Scholar
Fröberg, R., Gottlieb, C. and Häggkvist, R., ‘On numerical semigroups’, Semigroup Forum 35 (1987), 63–83.CrossRefGoogle Scholar
García-Sánchez, P. A., ‘An overview of the computational aspects of nonunique factorization invariants’ in: Multiplicative Ideal Theory and Factorization Theory–Commutative and Non-Commutative Perspectives, Springer Proceedings in Mathematics and Statistics, 170 (Springer, Switzerland, 2016).Google Scholar
García-Sánchez, P. A. and Ojeda, I., ‘Uniquely presented finitely generated commutative monoids’, Pacific J. Math. 248(1) (2010), 91–105.Google Scholar
Herzog, J., ‘Generators and relations of abelian semigroups and semigroup rings’, Manuscripta Math. 3 (1970), 175–193.Google Scholar
Katsabekis, A. and Ojeda, I., ‘An indispensable classification of monomial curves in ${\mathbb{A}}^4\left(\mathbb{k}\right)$ ’, Pacific J. Math. 268(1) (2014), 96–116.CrossRefGoogle Scholar
Marquez-Campos, G., Ojeda, I. and Tornero, J. M., ‘On the computation of the Apery set of numerical monoids and affine semigroups’, Semigroup Forum 91(1) (2015), 139–158.CrossRefGoogle Scholar
Migliore, J. C., Progress in Mathematics, Vol. 165 (Birkhäuser, Boston, MA, 1998).Google Scholar
Miller, E. and Sturmfels, B., Combinatorial Commutative Algebra, Graduate Texts in Mathematics, Vol. 227 (Springer-Verlag, New York, 2005).Google Scholar
Northcott, D.G., ‘A homological investigation of a certain residual ideal’, Math. Ann. 150 (1963), 99–110.CrossRefGoogle Scholar
O’Carroll, L. and Planas-Vilanova, F., ‘Ideals of Herzog–Northcott type’, Proc. Edinb. Math. Soc. 54 (2011), 161–186.CrossRefGoogle Scholar
Ojeda, I. and Piedra-Sánchez, R., ‘Cellular binomial ideals. Primary decomposition of binomial ideals’, J. Symbolic Comput. 30(4) (2000), 383–400.Google Scholar
Ojeda, I. and Pisón-Casares, P., ‘On the hull resolution of an affine monomial curve’, J. Pure Appl. Algebra 192 (2004), 53–67.Google Scholar
Ojeda, I. and Vignerón-Tenorio, A., ‘Indispensable binomials in semigroup ideals’, Proc. Amer. Math. Soc. 138 (2010), 4205–4216 CrossRefGoogle Scholar
Ojeda, I. and Vignerón-Tenorio, A., ‘The short resolution of a semigroup algebra’, Bull. Aust. Math. Soc. 96(3) (2017), 400–411.CrossRefGoogle Scholar
Rosales, J. C., ‘On presentations of subsemigroups of ${\mathbb{N}}^{\mathrm{n}}$ ’, Semigroup Forum 55(2) (1997), 152–159.CrossRefGoogle Scholar
Rosales, J. C. and García Sánchez, P. A., Finitely Generated Commutative Monoids (Nova Science Publishers, Inc., Commack, NY, 1999).Google Scholar
Rosales, J. C. and García Sánchez, P. A., Numerical Semigroups, Publisher Developments in Mathematics, 20 (Springer, New York, 2009).CrossRefGoogle Scholar
Sturmfels, B., Gröbner Bases and Convex Polytopes, University Lecture Series, 8 (American Mathematical Society, Providence, RI, 1996).Google Scholar
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.7.5, 2014 (http://www.gap-system.org).Google Scholar
Vasconcelos, W. V., Computational Methods In Commutative Algebra And Algebraic Geometry, Algorithms and Computation in Mathematics, 2 (Springer-Verlag, Berlin–Heidelberg, 1998).CrossRefGoogle Scholar
Wilf, H. S., ‘A circle-of-lights algorithm for the “money-changing problem”’  Amer. Math. Monthly 85 (1978), 562–565.Google Scholar