Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-05-25T20:27:11.092Z Has data issue: false hasContentIssue false
  • English
  • Français

The chromatic number of the sphere

Published online by Cambridge University Press:  09 April 2009

Gustavus J. Simmons
Gustavus J. Simmons
Affiliation:
Department of Mathematics Sandia Laboratories Albuquerque, New Mexico, 87115, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Erdös, Harary and Tutte have defined the chromatic number of the plane to be the least number of sets partitioning the plane such that no set contains two points at unit distance apart. By analogy, the chromatic number χ(S1), of the sphere, Sr of radius r is defined to be the least number of sets partitioning the surface of Sr such that no set contains two points at unit chordal distance apart. In this paper it is proven that and that this bound is best possible since .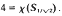

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 21 , Issue 4 , June 1976 , pp. 473 - 480
Copyright
Copyright © Australian Mathematical Society 1976

References

Erdös, P., Harary, F. and Tutte, W. T. (1965), ‘On the dimension of a graph’, Mathematika 12, 118–122.CrossRefGoogle Scholar
Hadwiger, H., Debrunner, H. and Klee, V. (1964), Combinatorial Geometry in the Plane, Holt, Rinehart & Winston, New York.Google Scholar
Moser, L. and Moser, W. (1961), ‘Problem and solution P10’, Canad. Math. Bull. 4, 187–189.Google Scholar
Simmons, G. J. (1974), On a problem of Erdös concerning a 3-coloring of the unit sphere, Discrete Math. 8, 81–84.CrossRefGoogle Scholar
Woodall, D. R., (1973), ‘Distances realized by sets covering the plane’, J. Combinatorial Theory Series A 14, 187–200.CrossRefGoogle Scholar