No CrossRef data available.
Article contents
A WEIGHTED 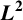 $\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
$\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
Published online by Cambridge University Press: 15 January 2024
Abstract
Let H be the Hermite operator 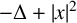 $-\Delta +|x|^2$ on
$-\Delta +|x|^2$ on 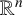 $\mathbb {R}^n$. We prove a weighted
$\mathbb {R}^n$. We prove a weighted 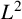 $L^2$ estimate of the maximal commutator operator
$L^2$ estimate of the maximal commutator operator 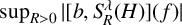 $\sup _{R>0}|[b, S_R^\lambda (H)](f)|$, where
$\sup _{R>0}|[b, S_R^\lambda (H)](f)|$, where 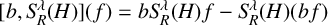 $ [b, S_R^\lambda (H)](f) = bS_R^\lambda (H) f - S_R^\lambda (H)(bf) $ is the commutator of a BMO function b and the Bochner–Riesz means
$ [b, S_R^\lambda (H)](f) = bS_R^\lambda (H) f - S_R^\lambda (H)(bf) $ is the commutator of a BMO function b and the Bochner–Riesz means 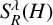 $S_R^\lambda (H)$ for the Hermite operator H. As an application, we obtain the almost everywhere convergence of
$S_R^\lambda (H)$ for the Hermite operator H. As an application, we obtain the almost everywhere convergence of 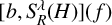 $[b, S_R^\lambda (H)](f)$ for large
$[b, S_R^\lambda (H)](f)$ for large 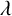 $\lambda $ and
$\lambda $ and  $f\in L^p(\mathbb {R}^n)$.
$f\in L^p(\mathbb {R}^n)$.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Ji Li
P. Chen and X. Lin were supported by National Key R&D Program of China 2022YFA1005702. P. Chen was supported by NNSF of China 12171489, Guangdong Natural Science Foundation 2022A1515011157.





