Hostname: page-component-7dc689bd49-bfm8c Total loading time: 0 Render date: 2023-03-20T23:51:52.550Z Has data issue: true Feature Flags: { "useRatesEcommerce": false } hasContentIssue true
  • English

DENSE STABLE RANK AND RUNGE-TYPE APPROXIMATION THEOREMS FOR 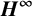${\boldsymbol H}^{\boldsymbol{\infty}}$ MAPS

Part of: Spaces and algebras of analytic functions

Published online by Cambridge University Press:  12 May 2021

ALEXANDER BRUDNYI
ALEXANDER BRUDNYI*
Affiliation:
Department of Mathematics and Statistics, University of Calgary, Calgary, Alberta, CanadaT2N 1N4
*
e-mail: albru@math.ucalgary.ca
Get access Rights & Permissions[Opens in a new window]

Abstract

Let 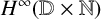$H^\infty ({\mathbb {D}}\times {\mathbb {N}})$ be the Banach algebra of bounded holomorphic functions defined on the disjoint union of countably many copies of the open unit disk 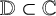${\mathbb {D}}\subset {{\mathbb C}}$ . We show that the dense stable rank of 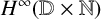$H^\infty ({\mathbb {D}}\times {\mathbb {N}})$ is 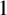$1$ and, using this fact, prove some nonlinear Runge-type approximation theorems for 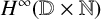$H^\infty ({\mathbb {D}}\times {\mathbb {N}})$ maps. 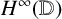Then we apply these results to obtain a priori uniform estimates of norms of approximating maps in similar approximation problems for the algebra $H^\infty ({\mathbb {D}})$ .

Keywords

bounded holomorphic functionBanach algebradense stable rankmaximal ideal spaceOka manifoldopen polyhedronRunge theorem

MSC classification

Secondary: 30H05: Bounded analytic functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 113 , Issue 3 , December 2022 , pp. 289 - 317
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Finnur Larusson

This research is supported in part by NSERC Grant No. 10010444.

References

Akhiezer, D. N., ‘Homogeneous complex manifolds’, in: Several Complex Variables IV , Encyclopaedia of Mathematical Sciences, 10 (eds. Gindikin, S. G. and Khenkin, G. M.) (Springer-Verlag, New York, 1990).Google Scholar
Bass, H., ‘K-theory and stable algebra’, Publ. Math. Inst. Hautes Études Sci. 22 (1964), 5–60.Google Scholar
Behrens, M., ‘The corona conjecture for a class of infinitely connected domains’, Bull. Amer. Math. Soc. 76(2) (1970), 387–391.CrossRefGoogle Scholar
Brudnyi, A., ‘Stein-like theory for Banach-valued holomorphic functions on the maximal ideal space of ${H}^{\infty }$ ’, Invent. Math. 193 (2013), 187–227.CrossRefGoogle Scholar
Brudnyi, A., ‘Oka principle on the maximal ideal space of ${H}^{\infty }$ ’, Algebra i Analiz 31(5) (2019), 24–89.Google Scholar
Brudnyi, A., ‘Structure of the maximal ideal space of ${H}^{\infty }$ on the countable disjoint union of open disks’, Algebra i Analiz 32(6) (2020), 58–71.Google Scholar
Brudnyi, A., ‘On stable rank of ${H}^{\infty }$ on coverings of finite bordered Riemann surfaces’, Rev. Mat. Iberoam., to appear, Preprint, 2020, arXiv:2007.05420.Google Scholar
Corach, G. and Larotonda, A. R., ‘Stable range in Banach algebras’, J. Pure Appl. Algebra 32 (1984), 289–300.CrossRefGoogle Scholar
Corach, G. and Suárez, F. D., ‘Extension problems and stable rank in commutative Banach algebras’, Topology Appl. 21 (1985), 1–18.CrossRefGoogle Scholar
Corach, G. and Suárez, F. D., ‘Dense morphisms in commutative Banach algebras’, Trans. Amer. Math. Soc. 304 (1987), 537–547.CrossRefGoogle Scholar
Forstnerič, F., ‘Complements of Runge domains and holomorphic hulls’, Michigan Math. J. 41 (1993), 297–308.Google Scholar
Forstnerič, F., Stein Manifolds and Holomorphic Maps , Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], 56 (Springer, New York, 2011).CrossRefGoogle Scholar
Garnett, J. B., Bounded Analytic Functions (Academic Press, New York, 1981).Google Scholar
Gunning, R. C. and Rossi, H., Analytic Functions of Several Complex Variables (Prentice Hall, Englewood Cliffs, NJ, 1965).Google Scholar
Hu, S.-T., ‘Some homotopy properties of topological groups and homogeneous spaces’, Ann. of Math. 49 (1948), 67–74.CrossRefGoogle Scholar
Hu, S.-T., ‘Mappings of a normal space into an absolute neighborhood retract’, Trans. Amer. Math. Soc. 64 (1948), 336–358.CrossRefGoogle Scholar
Hu, S.-T., Homotopy Theory (Academic Press, New York, 1959).Google Scholar
Husemoller, D., Fibre Bundles (Springer-Verlag, New York, 1994).CrossRefGoogle Scholar
Kusakabe, Y., Oka properties of complements of holomorphically convex sets, Preprint, 2020, arXiv:2005.08247.Google Scholar
Suárez, D., ‘Čech cohomology and covering dimension for the ${H}^{\infty }$ maximal ideal space’, J. Funct. Anal. 123 (1994), 233–263.Google Scholar
Suárez, D., ‘Approximation by ratios of bounded analytic functions’, J. Funct. Anal. 160 (1998), 254–269.Google Scholar
Taylor, J. L., ‘Topological invariants of the maximal ideal space of a Banach algebra’, Adv. Math. 19 (1976), 149–206.CrossRefGoogle Scholar
Tolokonnikov, V., ‘Stable rank of ${H}^{\infty }$ in multiply connected domains’, Proc. Amer. Math. Soc. 123(10) (1995), 3151–3156.Google Scholar
Treil, S., ‘Stable rank of ${H}^{\infty }$ is equal to one’, J. Funct. Anal. 109 (1992), 130–154.Google Scholar
Vaserstein, L. N., ‘The stable range for rings and the dimension of topological spaces’, Funct. Anal. Appl. 5 (1971), 102–110.CrossRefGoogle Scholar